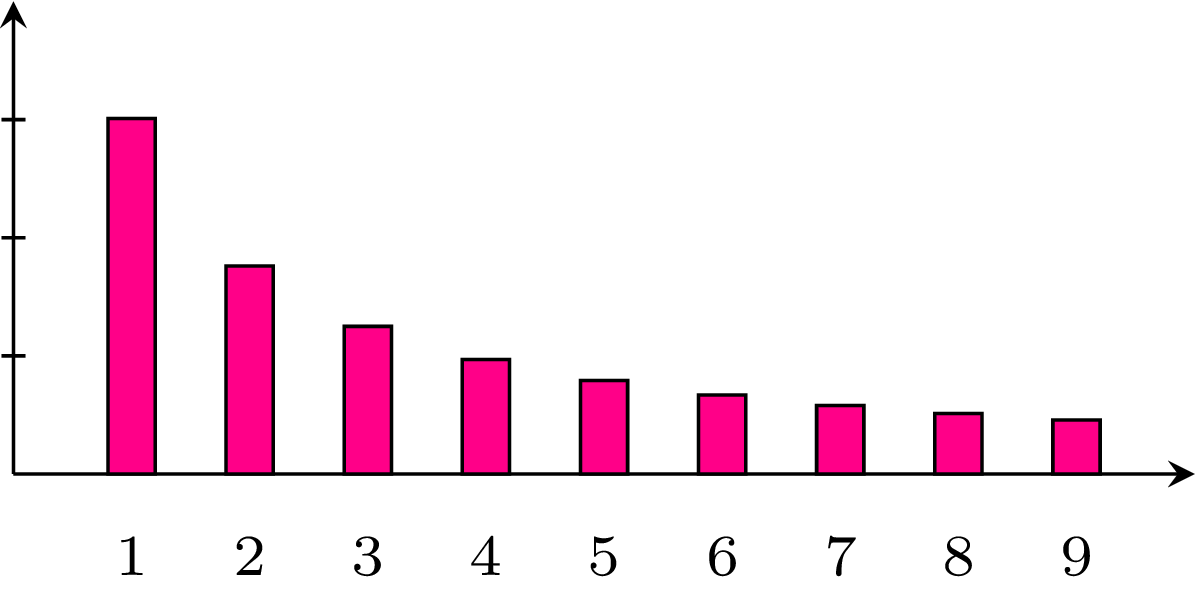Afiliacja: Coláiste an Spioraid Naoimh, University College Cork Maths Enrichment Program
Po raz pierwszy natknąłem się na prawo Benforda podczas lektury pewnej książki z matematycznymi ciekawostkami. Zafascynowały mnie prostota i ogólność tej zasady – zwłaszcza że na pierwszy rzut oka wydała mi się zaskakująca, wręcz oderwana od rzeczywistości.
Czym zatem jest prawo Benforda? To interesujące i dla wielu sprzeczne z intuicją zjawisko statystyczne występujące w zbiorach danych, które obejmują kilka rzędów wielkości. Jego podstawowym objawem jest to, że pierwsza cyfra liczb w takich zbiorach znacznie częściej jest mała (np. 1 lub 2) niż duża (np. 8 lub 9). Innymi słowy: częstość występowania poszczególnych cyfr jest zauważalnie przesunięta w stronę mniejszych wartości. Zgodnie z tym prawem cyfra 1 pojawia się jako pierwsza w około \(30\%\) przypadków, podczas gdy cyfra 9 jedynie w \(5\%\)! W ogólności prawo Benforda stwierdza, że częstotliwość występowania na pierwszym miejscu cyfry \(d\) w danych zapisanych w systemie dziesiętnym, obejmujących kilka rzędów wielkości, jest równa w przybliżeniu \(\log_{10}(d+1)-\log_{10}d\) (rys. 1). Określone tym wzorem częstości występowania noszą nazwę rozkładu Benforda.
Rys. 1. Częstości występowania poszczególnych cyfr według prawa Benforda
Zakres stosowalności prawa Benforda jest zaskakująco szeroki: może dotyczyć zarówno wysokości stu najwyższych budynków, jak i długości rzek. Pojawia się także w czysto matematycznych kontekstach – rozkład Benforda odnajdziemy wśród pierwszych cyfr ciągu Fibonacciego, kolejnych potęg liczby 2 czy ciągu powstałego przez naprzemienne mnożenie przez 2 i 3. Należy tu zaznaczyć, że choć warunek ,,obejmowania kilku rzędów wielkości” wygląda niepozornie, to jest niezwykle istotny. Dla przykładu, liczba stron w książkach nie spełnia prawa Benforda, ponieważ zdecydowana większość książek ma od 200 do 600 stron.
Po usłyszeniu o prawie Benforda po raz pierwszy byłem zdumiony – jak coś tak jawnie asymetrycznego może być aż tak powszechne? Niniejszy artykuł ma na celu przedstawienie intuicyjnego, a po części również formalnego, wyjaśnienia, dlaczego to prawo obowiązuje. Opowiemy także o jego historii oraz zaskakujących zastosowaniach.
Po raz pierwszy prawo Benforda zostało odkryte w 1881 roku przez… Simona Newcomba, kanadyjsko-amerykańskiego astronoma. Zauważył on, że początkowe strony tablic logarytmicznych, używanych do obliczeń, były znacznie bardziej zużyte niż końcowe. Wysunął hipotezę, że powodem był fakt, iż dane, na których naukowcy przeprowadzali obliczenia, miały tendencję do zawierania liczb o niższych początkowych cyfrach. Newcomb opublikował w American Journal of Mathematics krótką notatkę na temat tego zjawiska, zawierającą teoretyczne prawdopodobieństwa wystąpienia kolejnych cyfr, a także nieformalny argument wyjaśniający jego prawdziwość. Notatka nie zyskała jednak większego rozgłosu.
Ponad pięćdziesiąt lat później, w roku 1938, prawo to zostało niezależnie odkryte na nowo przez Franka Benforda. Benford pracował jako fizyk w firmie General Electric, gdy dostrzegł ten sam wzorzec w taki sam sposób jak wcześniej Newcomb (tzn. przez inspekcję tablic logarytmicznych). Poszedł on jednak o krok dalej w swojej analizie i zebrał dane dotyczące kilkunastu różnych cech (np. populacje państw), obejmujące łącznie ponad 20 000 obserwacji. Wykorzystał je w artykule, który opublikował w Proceedings of the American Philosophical Society, trafnie zatytułowanym ,,The Law of Anomalous Numbers”. Nazwa ta się nie przyjęła, a prawo zostało nazwane na cześć Benforda, co stanowi kolejny przykład działania tzw. prawa Stiglera w świecie matematyki.
Prawo Stiglera mówi, że odkrycia względnie rzadko noszą nazwiska osób, które ich dokonały. Jednym z przykładów jest właśnie prawo Stiglera.
W tym momencie Czytelnik może wciąż być sceptyczny wobec zasadności prawa Benforda – ale to, co na pierwszy rzut oka może wydawać się niedorzeczne, na szczęście ma proste i intuicyjne wyjaśnienie. Załóżmy, że mamy zbiór liczb obejmujących wiele rzędów wielkości. Powiedzmy, że oczekujemy, iż dane są równomiernie rozłożone pomiędzy możliwymi rzędami wielkości – np. w przedziale \([100, 1000]\) znajduje się mniej więcej tyle samo elementów co w przedziale \([1000,10\,000].\) Na skali logarytmicznej te dwa przedziały mają tę samą długość \(\log_{10} 10=1.\) Przez ekstrapolację możemy oczekiwać, że dla dowolnych dwóch odcinków o równej długości na skali logarytmicznej liczba elementów w każdym z nich jest mniej więcej taka sama. Innymi słowy – oczekujemy, że punkty odpowiadające danym są równomiernie rozłożone na skali logarytmicznej. Zbiór liczb, których reprezentacja w systemie dziesiętnym zaczyna się od cyfry \(d,\) jest rozłączną sumą odcinków o długości \({\log_{10}(d+1)-\log_{10}d},\) co prowadzi nas do prawdopodobieństw opisanych przez prawo Benforda.
Odsyłamy Czytelnika do artykułu Od mnożenia do dodawania (\(\Delta^{1}_{25}\)) w celu uzyskania dodatkowych interesujących informacji na temat skali logarytmicznej.
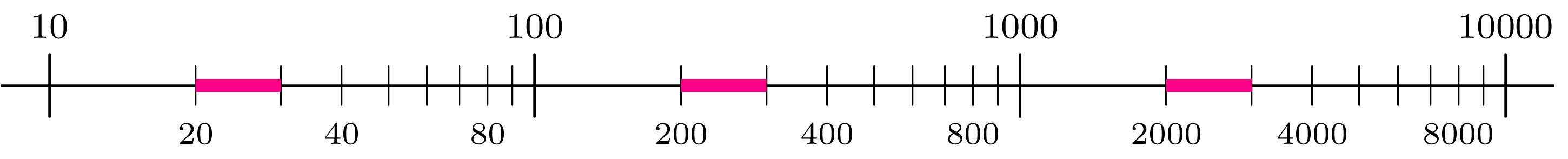
Rys. 2. Kolorowe odcinki o długości \(\log_{10}(3/2)\) odpowiadają liczbom, których pierwszą cyfrą jest cyfra 2
Zaznaczmy, że powyższe rozumowanie nie stanowi pełnego dowodu poprawności prawa Benforda. Teoretycy mogą protestować, że nie istnieje ,,równomierny rozkład” na całej, nieskończonej skali logarytmicznej, zaś praktycy zapytają, czemu w ogóle koncentrujemy się na równomiernym rozkładzie w skali logarytmicznej – czy jest to prawo przyrody, czy może wynika to również z matematycznych twierdzeń z rodzaju centralnego twierdzenia granicznego? Czytelnikom, którzy czują w tym względzie niedosyt, polecamy artykuł Teda Hilla A Statistical Derivation of the Significant-Digit Law, opublikowany w ,,Statistical Science” w 1995 roku.
Jak na obserwację natury matematycznej, prawo Benforda ma zaskakująco wiele bezpośrednich zastosowań. Najważniejsze z nich dotyczą wykrywania oszustw – można go użyć jako wstępnego testu w celu wykrycia ewentualnych nieprawidłowości. Liczby zawarte w księgach rachunkowych zazwyczaj spełniają prawo Benforda, gdyż faktycznie często obejmują kilka rzędów wielkości. Jeżeli natomiast księgi zawierałyby sfałszowane liczby generowane losowo przez komputer lub ręcznie, to można wtedy oczekiwać dość równomiernego rozkładu cyfr wiodących (czyli innego niż rozkład Benforda). Po pierwszym zetknięciu się z prawem Benforda śledczy finansowy Darrell D. Dorrell natychmiast zaczął stosować je w prowadzonych przez siebie sprawach. Doprowadziło to do skutecznego skazania doradcy finansowego Wesley’a Rhodesa, który zdefraudował miliony dolarów z funduszy swoich inwestorów. Prawo Benforda jest regularnie wykorzystywane jako pierwszy wskaźnik lub sygnał ostrzegawczy dotyczący oszustw finansowych – jeśli liczby w rejestrach bankowych go nie spełniają, oznacza to, że warto dokonać ich dokładniejszej analizy.
Innym, niezwykle interesującym zastosowaniem było odkrycie ukrytej sieci botów na Twitterze. Badanie takie wykonała Informatyczka Jennifer Golbeck w 2015 roku. Dla testowanego konta sprawdzano, ile obserwujących ma każde z kont, które je obserwuje, a następnie badano, czy otrzymane liczby pochodzą z rozkładu Benforda. W większości przypadków otrzymano zgodność. Jednak niewielki odsetek badanych kont nie wykazywał zgodności z tym wzorcem. Wskazano 170 takich kont do dalszego zbadania poprzez analizę historii postów oraz kont obserwujących. Spośród wszystkich 170 kont jedynie 2 wydawały się należeć do prawdziwych użytkowników. Reszta kont miała obserwujących wśród pozostałych podejrzanych kont i publikowała wyraźnie zautomatyzowane lub budzące podejrzenia posty.
Jak już podkreślaliśmy, prawo Benforda nie stosuje się do każdego rodzaju danych. Dobrym i nieoczywistym przykładem jest wykrywanie fałszerstw wyborczych. Przyczyna jest następująca: okręgi wyborcze zazwyczaj mają podobną liczbę mieszkańców. Jeśli więc jeden kandydat oczekuje uzyskania określonego poparcia w każdym z tych okręgów, rozkład pierwszych cyfr będzie ograniczony do zakresu, który niekoniecznie pasuje do prawa Benforda. Po wyborach prezydenckich w USA w 2020 roku zwolennicy teorii spiskowych zauważyli, że liczba głosów oddanych na Joe Bidena w niektórych okręgach nie spełniała prawa Benforda. Traktowali tę obserwację jako dowód na sfałszowanie wyborów, jednak – z powodów wymienionych powyżej – ich wątpliwości nie były uzasadnione. Podobną ostrożność należy zachować w przypadku oszustw finansowych – jeśli firma sprzedaje dużą liczbę produktów w tej samej cenie, rozkład cyfr w rachunkach będzie skupiony wokół pierwszej cyfry tej ceny.
Na koniec dodajmy, że prawo Benforda można również sformułować dla drugiej cyfry znaczącej. Wówczas rozkład prawdopodobieństwa wystąpienia kolejnych cyfr jest bardziej ,,płaski” – w tym przypadku różnica w częstości występowania między 0 a 9 wynosi już tylko około \(3\) punktów procentowych – ale nadal powinna być zauważalna w wystarczająco dużych zbiorach danych. W zastosowaniu prawa Benforda do wyborów to właśnie to uogólnienie, w połączeniu z prawem dla pierwszej cyfry, pozwala na znacznie bardziej wiarygodny test, czy doszło do oszustwa. Na drugą cyfrę nie ma już (tak dużego) wpływu podobieństwo populacji wyborców pomiędzy okręgami wyborczymi. Co nie zaskakuje, rozkład dla \(n\)-tej cyfry staje się coraz bardziej płaski wraz ze wzrostem \(n.\)
Można dość prosto uzasadnić, że prawo Benforda zostaje zachowane, gdy dane zostaną wyrażone w innych jednostkach lub w systemie o innej podstawie liczbowej. Ta tematyka jest bogata w ciekawe wyniki – innym fascynującym przykładem jest prawo Zipfa dotyczące częstości występowania słów w tekstach. Nadal jestem zaskoczony za każdym razem, gdy prawo Benforda pojawia się w moim codziennym życiu – jeśli zaczniesz go szukać, możesz zacząć dostrzegać przykłady wszędzie wokół siebie!