Afiliacja: Uczeń, Colegiul Național de Informatică Tudor Vianu, Rumunia
W tym artykule zajmiemy się następującym zagadnieniem.
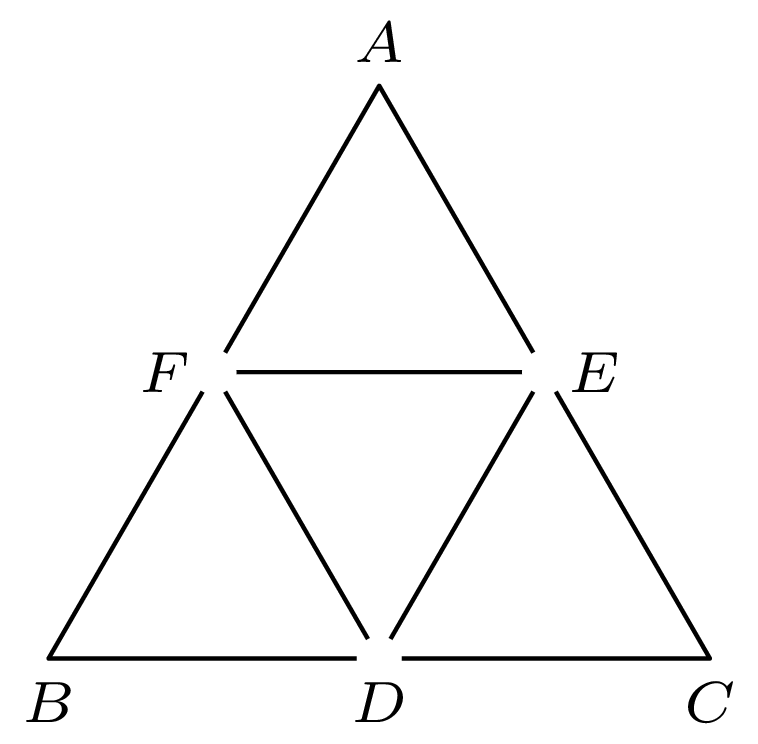
Policjanci gonią złodzieja w pewnej wiosce, której uliczki tworzą trójkąt równoboczny wraz z jego środkowymi (rys. 1). Maksymalna prędkość złodzieja jest \(\kappa>0\) razy większa niż maksymalna prędkość policjantów. Zakładając, że wszyscy stale się widzą i ruch jest możliwy jedynie wzdłuż uliczek, należy określić, czy policjanci mogą schwytać złodzieja niezależnie od ich początkowego ustawienia.
Rys. 1
Rozpocznijmy rozwiązanie od analizy kilku prostych przypadków. Oznaczmy liczbę policjantów przez \(n.\) Załóżmy, że w wiosce znajduje się tylko jeden policjant, tj. \(n=1.\) To banalny przypadek. Jeśli \(\kappa < 1\) (tzn. złodziej jest wolniejszy od policjanta), policjant na pewno doścignie i schwyta złodzieja. Analogicznie, jeśli \(\kappa \geq 1,\) to złodziej może dowolnie długo uciekać przed policjantem, choćby biegając w cyklu \(A \to B \to C \to A\) (rys. 1).
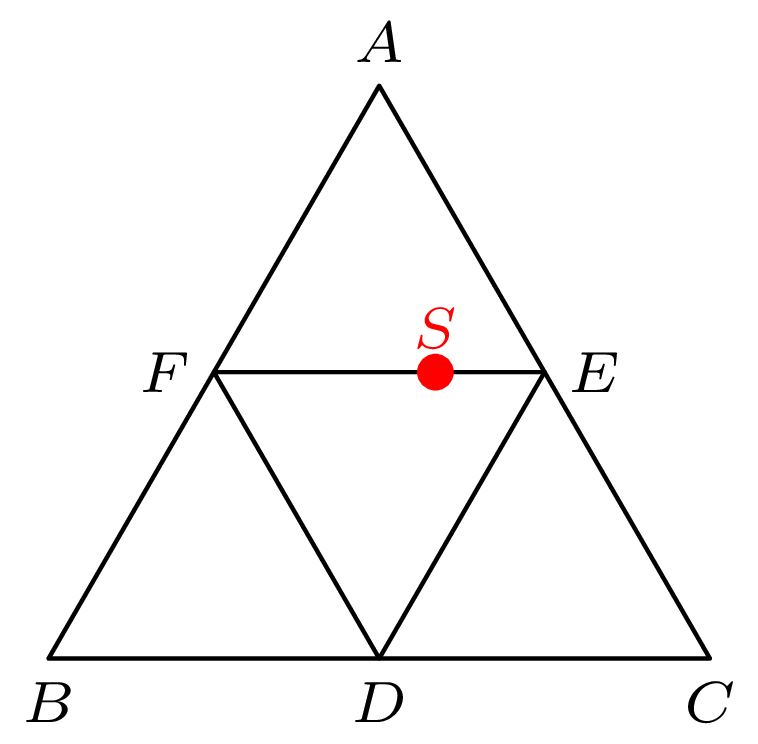
Sytuacja zmienia się diametralnie (na korzyść wymiaru sprawiedliwości), gdy w pościgu bierze udział trzech (lub więcej) policjantów. Udowodnimy, że w tym przypadku schwytają oni złodzieja niezależnie od jego prędkości. Jedna ze strategii, które do tego doprowadzą, polega na jednoczesnym zajęciu punktów \(D, E\) i \(F\) (oznaczenia z rys. 1). W ten sposób policjanci podzielą całą wioskę na sześć spójnych części (składowych), jak pokazano na rysunku 2. W jednej z tych części znajduje się złodziej. Na jej krańcach (podobnie jak każdej innej części) znajdują się policjanci. Wystarczy, aby jeden z nich zaczął poruszać się (w ramach tej części) w stronę drugiego, a złodziej zostanie złapany.
Rys. 2
Pozostaje rozważyć przypadek dwóch policjantów – ten jest bardziej wymagający. Udowodnimy najpierw, że dla \(\kappa \leq 3\) policjanci zawsze złapią złodzieja. W tym celu jeden z policjantów będzie stale gonił rabusia – tego policjanta nazwiemy gończym. Jego jedynym zadaniem jest uniemożliwienie złodziejowi przyczajenia się na stałe w jednym miejscu. Dokładniej rzecz ujmując, musi on zadbać o to, by ostatnio odwiedzony przez złodzieja punkt środkowy zmieniał się w czasie (punktami środkowymi są punkty \(D,\) \(E\) lub \(F\)). Łatwo się przekonać, że aby to osiągnąć, wystarczy tylko jeden policjant.
Drugi policjant, którego nazwiemy stróżem, ma bardziej subtelne zadanie. Najpierw musi udać się do ,,stróżówki” znajdującej się w punkcie \(S,\) który dzieli odcinek \(EF\) w stosunku \(1\!:\!2\) (rys. 3). Kiedy już tam dotrze, musi uważnie obserwować poczynania złodzieja. Zadaniem tego policjanta jest odcinanie drogi ucieczki złodzieja, gdy tylko jest to możliwe. Na przykład, jeśli złodziej wejdzie do ,,górnego naroża” \(E\!\mathrel{\unicode{x2013}}\!A \!\mathrel{\unicode{x2013}}\!F\) przez punkt \(E,\) stróż musi uniemożliwić mu ucieczkę przez punkt \(F.\) Ma taką możliwość, gdyż \(\frac{|EA|+|AF|}{|SF|}=3\geq \kappa.\) Jest też pewien mały haczyk – w tym samym momencie, w którym złodziej powróci do punktu \(E,\) stróż musi ponownie znaleźć się w punkcie \(S.\) Jest to jednak możliwe do zrealizowania, wystarczy, że stróż będzie poruszał się z prędkością dokładnie trzy razy mniejszą niż złodziej (z zachowaniem odpowiedniego kierunku).
Rys. 3
Oto pełna lista możliwości stróża w zakresie kontrolowania ruchu złodzieja:
-
jeśli złodziej wchodzi do \(E\!\mathrel{\unicode{x2013}}\!A \!\mathrel{\unicode{x2013}}\!F\) przez \(E,\) nie może uciec przez \(F,\)
-
jeśli złodziej wchodzi do \(E\!\mathrel{\unicode{x2013}}\!A \!\mathrel{\unicode{x2013}}\!F\) przez \(F,\) nie może uciec przez \(E,\)
-
jeśli złodziej wchodzi do \(D\!\mathrel{\unicode{x2013}}\!B \!\mathrel{\unicode{x2013}}\!F\) przez \(D,\) nie może uciec przez \(F,\)
-
jeśli złodziej wchodzi do \(D\!\mathrel{\unicode{x2013}}\!C \!\mathrel{\unicode{x2013}}\!E\) lub \(D\!\mathrel{\unicode{x2013}}\!E\) przez \(D,\) nie może uciec przez \(E.\)
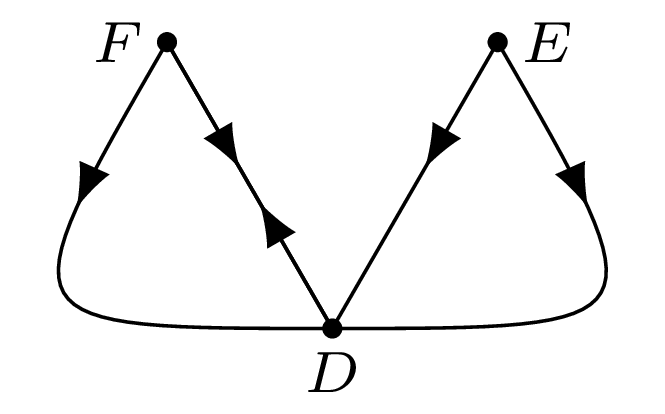
Jak już wiemy, gończy zmusza złodzieja do przechodzenia między punktami \(D,\) \(E\) i \(F.\) Warunki (a)–(d) nakładają poważne ograniczenia na kolejność, w jakiej punkty te będą odwiedzane:
Rys. 4
-
tylko punkt \(D\) może być odwiedzony bezpośrednio po \(E\) lub \(F,\)
-
tylko punkt \(F\) może być odwiedzony bezpośrednio po \(D,\) i to jedynie przez krawędź \(D\!\mathrel{\unicode{x2013}}\!F.\)
Te ograniczenia są zilustrowane na rysunku 4. Wynika stąd, że policjanci mogą zmusić złodzieja do biegania w cyklu \(D\to F\to D\)! Ale jak mogą go ostatecznie schwytać? Wystarczy przekazać gończemu jeszcze jedną instrukcję: ma on poruszać się po bokach trójkąta \(DFB\) tylko zgodnie z ruchem wskazówek zegara. Nie zmienia to jego zdolności do utrzymywania złodzieja w ruchu i zmuszania go do zmiany punktów środkowych, ale w ten sposób gończy w końcu go dopadnie, gdy ten zacznie już poruszać się w cyklu. To kończy uzasadnienie, że w tym przypadku policjanci mają strategię wygrywającą.
Zauważmy, że wbrew swojej nazwie gończy może poruszać się dowolnie wolno. Musi jednak cechować się niemałą wytrwałością.
Udowodnimy teraz, że dla \(\kappa > 3\) to złodziej jest na wygranej pozycji (przy odpowiednim początkowym ustawieniu). Zasadniczo jego strategia polega na rozpoczęciu w jednym z punktów \(D, E, F\) i przechodzeniu do innego z tych punktów za każdym razem, gdy zbliży się do niego któryś z policjantów. Spróbujmy opracować szczegóły tego podejścia.
Załóżmy, że złodziej zaczyna w węźle \(D.\) Będzie tam czekał, dopóki jeden z policjantów (ponownie nazwijmy go gończym) nie zbliży się do niego na odległość mniejszą niż, powiedzmy, \(\varepsilon=0{,}2\) (zakładamy \(|EF|=1\)). Wtedy złodziej próbuje przejść do \(E\) lub \(F.\) Bez straty ogólności załóżmy, że gończy zbliża się do złodzieja ze strony punktów \(B\) lub \(F.\) Przyjmijmy, że złodziej pokonuje odległość \(|EF|\) w minutę. Rozważmy następujące przypadki:
-
Jeśli drugi policjant uniemożliwia złodziejowi bezpośrednie przejście do \(F,\) to krawędź \(D\!\mathrel{\unicode{x2013}}\!E\) jest pusta, a zatem złodziej może dotrzeć do \(E\) w ciągu minuty – czyli szybciej niż każdy z policjantów (rys. 5).
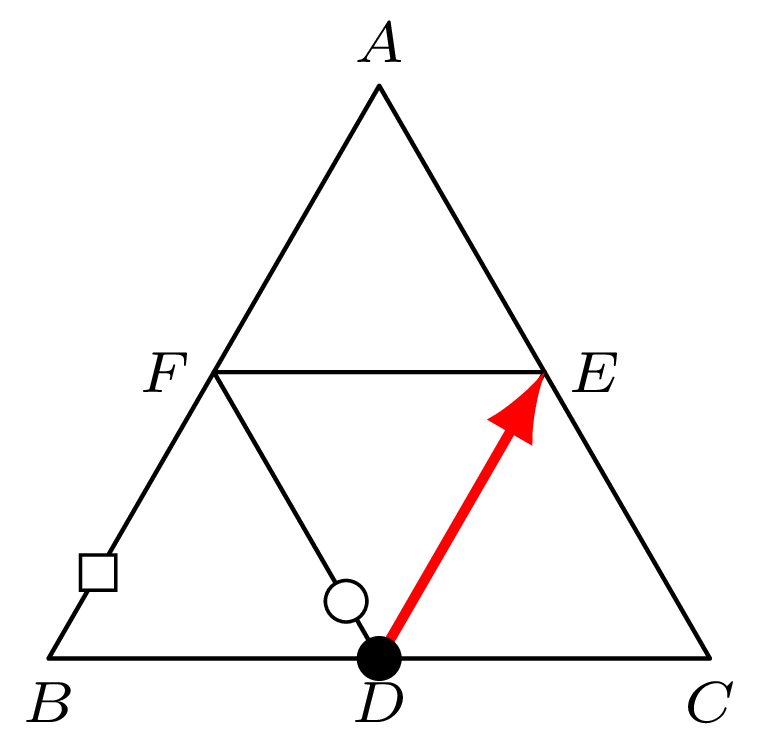
Rys. 5. Czarny punkt przedstawia złodzieja, zaś białe punkty – policjantów (gończy jest oznaczony kółkiem) -
Jeśli drugi policjant znajduje się na krawędzi \(D\!\mathrel{\unicode{x2013}}\!E,\) to złodziej może dotrzeć do \(F\) w ciągu dwóch minut, zanim dotrze tam którykolwiek z policjantów (rys. 6). Zauważmy, że jeśli gończy znajduje się na odcinku \(BD,\) to złodziej może dotrzeć do \(F\) w ciągu zaledwie jednej minuty, ale nie ma to znaczenia dla naszej analizy.
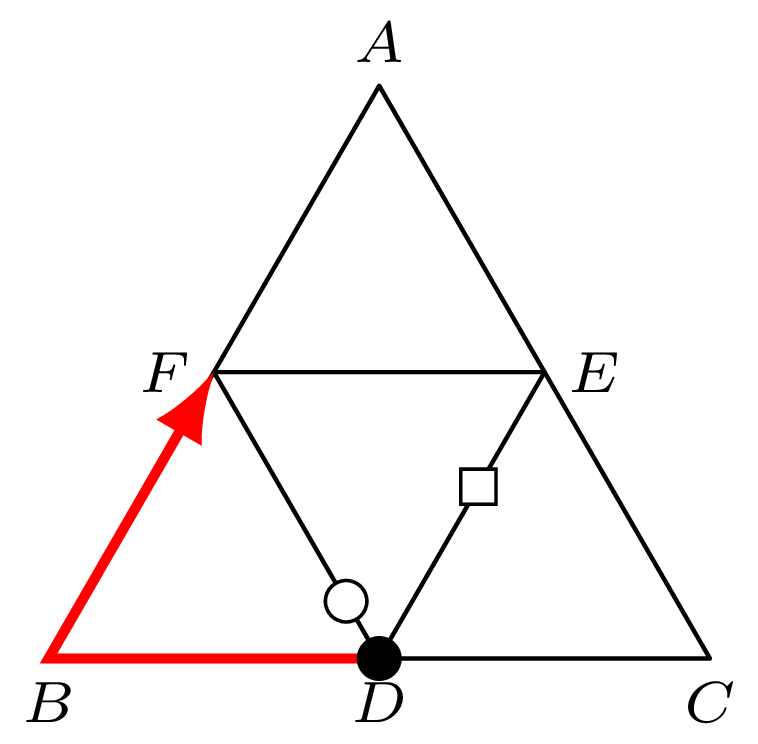
Rys. 6 -
W pozostałych przypadkach złodziej może bezpośrednio dotrzeć do \(E\) w minutę i do \(F\) maksymalnie w 2 minuty. Zauważmy, że gończy (który początkowo znajduje się blisko \(D\)) potrzebuje więcej niż 2 minuty, aby dotrzeć do dowolnego z tych punktów. Jeśli zaś chodzi o drugiego policjanta, rysunek 7 przedstawia dwa zbiory – jasnoniebieski to zbiór punktów, z których można dotrzeć do \(E\) w minutę, a jasnozielony to zbiór punktów, z których można dotrzeć do \(F\) w 2 minuty. Jasno widać, że przy założeniu \(\kappa>3\) te dwa zbiory nie przecinają się. Zatem złodziej może wybrać jeden z tych punktów, mając pewność, że dotrze tam przed drugim policjantem.
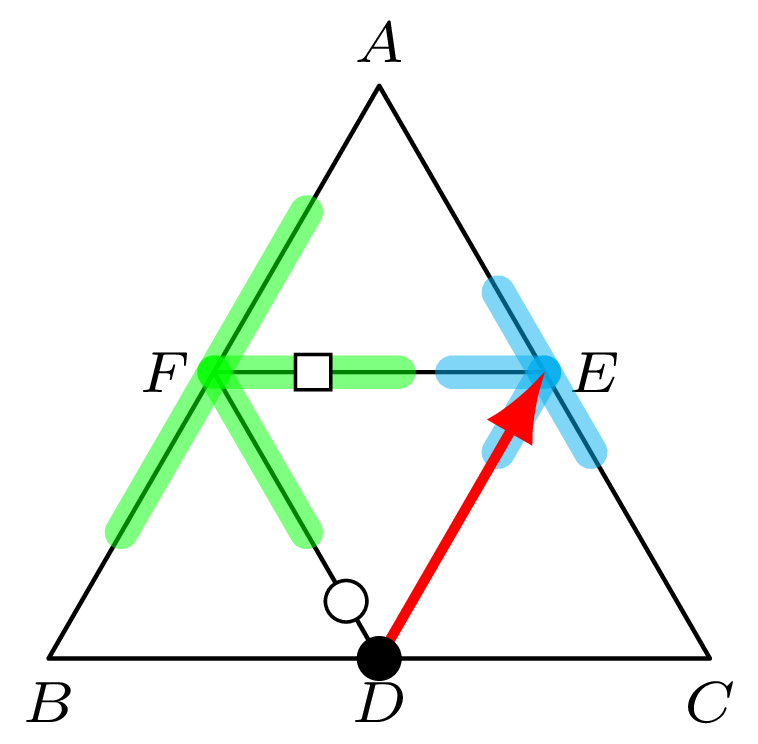
Rys. 7
Oczywiście, jeśli złodziej może raz dokonać zmiany punktu środkowego, to może tak robić w nieskończoność. Możemy więc stwierdzić, że złodziej ma strategię wygrywającą wtedy i tylko wtedy, gdy \(n = 1\) i \(\kappa \geq 1\) lub \(n = 2\) i \(\kappa > 3.\) Rzecz jasna, problem ten można uogólnić na inne kształty wiosek, takie jak siatka \(2 \times 2\) czy nawet siatka \(N \times M.\) Zachęcamy Czytelnika do przeanalizowania podobnych strategii dla tych przypadków.