Zadania z fizyki nr 772, 773
Termin nadsyłania rozwiązań: 30 IV 2024
Redaguje Elżbieta ZAWISTOWSKA
772. Rakieta jest rozpędzana w wyniku wyrzucania ciągłego strumienia gazu, którego prędkość względem rakiety jest stała i wynosi \(v_0.\) Początkowa prędkość rakiety jest równa zeru. Ile wynosi prędkość rakiety, gdy jej energia kinetyczna osiąga wartość maksymalną? Siłę ciężkości zaniedbujemy.
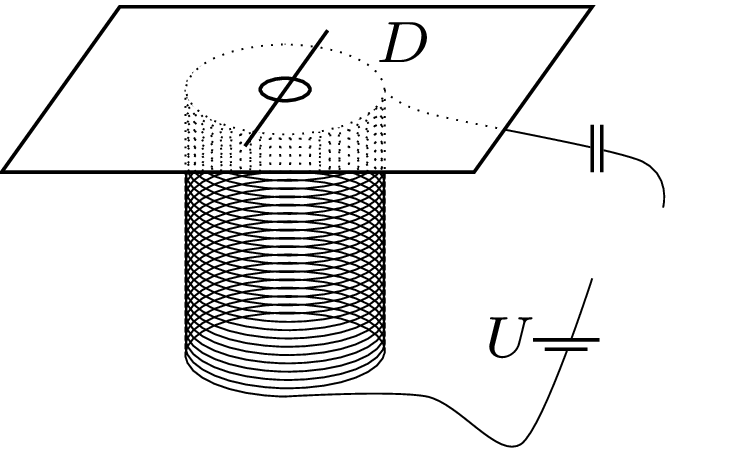
773. Na górze ustawionej pionowo zwojnicy leży cienki kawałek kartonu, a na nim mały nadprzewodzący pierścień z cienkiego drutu, którego średnica \(d_1\) jest znacząco mniejsza od średnicy pierścienia \(D\ \)(rys. 1). Po podłączeniu zwojnicy do źródła napięcia \(U\) szeregowo z kondensatorem pierścień podskakuje, gdy \(U>U_0.\) Jakie powinno być napięcie źródła w analogicznym doświadczeniu z pierścieniem o takiej samej średnicy, ale wykonanego z drutu o średnicy \(d_2\)? Współczynnik samoindukcji takiego pierścienia wynosi w przybliżeniu \(L= kDln\left(1,4D/d\right).\) Opór zwojnicy możemy pominąć.
Rozwiązania zadań z numeru 10/2023
Przypominamy treść zadań:
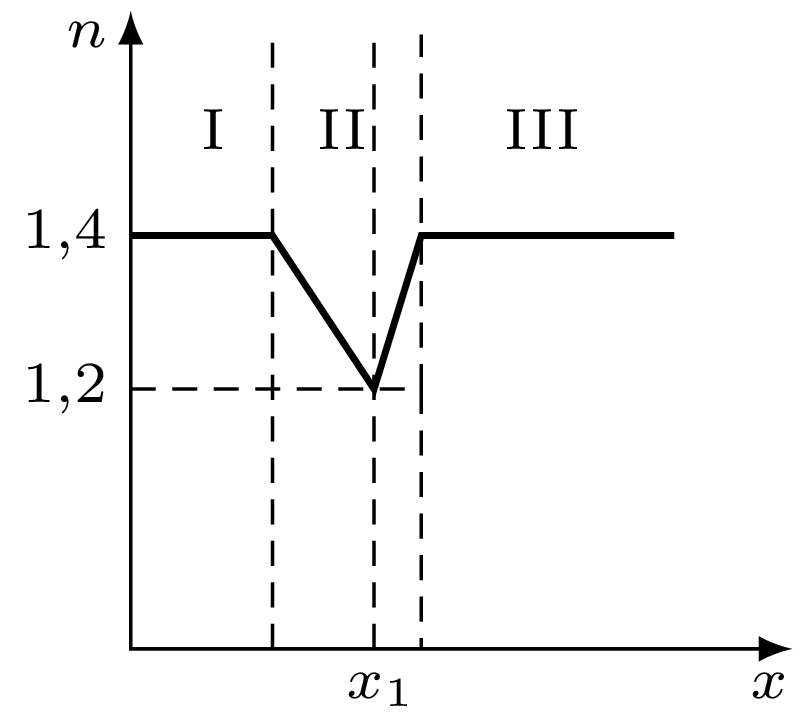
764. Na rysunku 2 pokazana jest zależność współczynnika \(n\) załamania ośrodków I, II i III od współrzędnej \(x.\) Wąska wiązka światła monochromatycznego pada na granicę rozdziału ośrodków I i II. Dla jakich kątów padania światło przejdzie do ośrodka III?
Z prawa załamania wynika, że wzdłuż trajektorii promienia wartość wyrażenia \(n\left(x\right)\sin{\alpha }_x\) nie zmienia się (\({\alpha }_x-\) kąt padania na granicę rozdziału, której odpowiada współrzędna \(x\)).
Ponieważ w drugim obszarze współczynnik początkowo maleje, kąty padania będą rosły w miarę zbliżania się do granicy, której odpowiada współrzędna \(x_1.\) Styczna do trajektorii promienia będzie zbliżać się do prostopadłej do osi \(x.\) Jeśli kąt padania w ośrodku II osiągnie wartość \({\pi }/{2},\) to promień nie wyjdzie z tego ośrodka. Natomiast jeśli kąt padania będzie mniejszy od \({\pi }/{2},\) nawet na granicy o współrzędnej \(x_1,\) gdzie współczynnik załamania osiąga minimalną wartość, promień przejdzie z obszaru II do III.
W przypadku granicznym mamy: \[n_1\sin{\alpha }_0=n\left(x_1\right)\sin{\pi \over 2}\ \Rightarrow \sin{\alpha }_0={1{,}2\over 1{,}4}\approx 0{,}86;\ \ {\alpha }_0\approx {\pi }/{3}.\] Wiązka światła przeniknie do obszaru III dla kątów padania \[0\le \alpha <{\pi }/{3.}\]
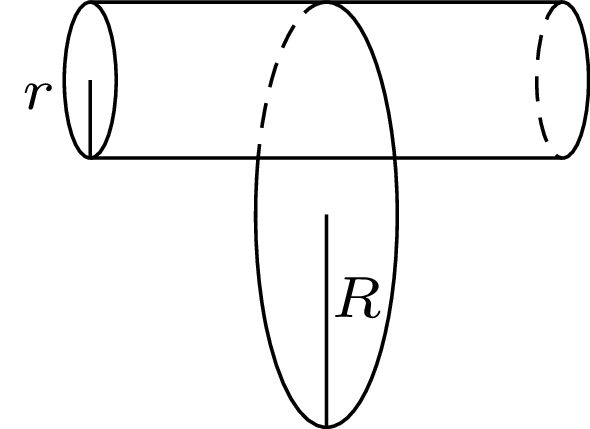
765. Na nieruchomy poziomy walec o promieniu \(r\) nałożona jest cienka obręcz o promieniu \(R\) (rys. 2). Znaleźć okres małych drgań obręczy w płaszczyźnie pionowej. Nie ma poślizgu między obręczą i walcem.
Tarcie jest statyczne, możemy więc skorzystać z zasady zachowania energii mechanicznej. Gdy środek obręczy odchylony jest z położenia równowagi o mały kąt \(\varphi\) (rys. 4), energia potencjalna układu ma postać: \[E_p=Mgh=Mg\left(R-r\right)\left(1-\cos\varphi \right)\cong Mg\left(R-r\right){{\varphi }^2}/{2,}\] gdzie \(M\) jest masą obręczy. Energia kinetyczna \(E_k\) jest sumą energii ruchu środka obręczy, który obraca się wokół osi walca z prędkością \(V,\) oraz energii ruchu obrotowego obręczy wirującej wokół środka masy w przeciwną stronę z prędkością \(v.\) Ponieważ nie ma poślizgu, \(V=v.\) Zatem \[E_k={MV^2\over 2}+{MR^2\over 2}{v^2\over R^2}=MV^2=M{\left(R-r\right)}^2{\left({d\varphi \over dt}\right)}^2.\] Różniczkując po czasie obie strony równania \(E_p+E_k=const,\) otrzymujemy równanie oscylatora harmonicznego: \[{d^2\varphi \over dt^2}+{g\over 2\left(R-r\right)}\varphi =0.\] Częstość małych drgań obręczy wynosi \(\omega =\sqrt{g/(2(R-r))},\) a okres drgań \(T=2\pi \sqrt{2(R-r)/g}.\)
Zadanie możemy też rozwiązać, traktując ruch środka obręczy jako czysty obrót wokół chwilowej osi obrotu przechodzącej przez punkt styczności z walcem A (rys. 4). Równanie ruchu obrotowego ma postać: \[2MR^2\varepsilon =-MgR\sin\varphi \approx -MgR\varphi ,\] stąd przyspieszenie kątowe \(\varepsilon =-{g\varphi }/{2R},\) a przyspieszenie liniowe \(a=\varepsilon R.\) Z drugiej strony \(a=\left(R-r)\right){d^2\varphi }/{dt^2}.\) Porównując oba wyrażenia na \(a,\) otrzymujemy takie samo jak poprzednio równanie oscylatora harmonicznego.
Rys. 1
Rys. 2
Rys. 3
Rys. 4
Czołówka ligi zadaniowej Klub 44 F po zakończeniu roku szkolnego 2022/2023 i po sprawdzeniu zadań 760 (\(WT = 2{,}6\)), 761 (\(WT = 1{,}83\))
Tomasz Rudny (Poznań) 43,41 Marian Łupieżowiec (Gliwice) 2–40,56 Jacek Konieczny (Poznań) 38,28 Tomasz Wietecha (Tarnów) 16–37,54 Konrad Kapcia (Poznań) 2–35,60 Ryszard Woźniak (Kraków) 32,96 Ryszard Baniewicz (Włocławek) 1–29,40 Andrzej Nowogrodzki (Chocianów) 3–20,97 Paweł Perkowski (Ożarów Maz.) 5–20,95 Paweł Kubit (Kraków) 15,73 Krzysztof Magiera (Łosiów) 4–13,42 Jan Zambrzycki (Białystok) 4–11,93 Lista obejmuje uczestników ligi, których stan konta wynosi przynajmniej 10 punktów i którzy przysłali rozwiązanie co najmniej jednego zadania z rocznika 2021, 2022 lub 2023.
Podsumowanie ligi zadaniowej Klubu 44 F w roku szkolnym 2022/2023
Średni współczynnik trudności zadań w omawianym okresie ma wartość 2,66. W przypadku pięciu z nich jest większy od trzech.
Nie było poprawnych rozwiązań zadania 745 (\(WT = 3{,}85\)) z kinematyki relatywistycznej. Należało w nim znaleźć prędkość pręta poruszającego się wzdłuż swojej osi, którego długość, widziana pod zadanym kątem przez odległego obserwatora, była równa jego długości spoczynkowej. W rozwiązaniu trzeba było uwzględnić skrócenie długości pręta w układzie spoczywającego obserwatora oraz fakt, że światło docierające do niego w tym samym momencie z obu końców pręta przebywa różne drogi. Wysyłane jest wcześniej z bardziej oddalonego końca pręta, a pręt przemieszcza się do chwili wysłania sygnału z bliższego końca.
W zadaniu 749 (\(WT = 3{,}47\)) należało obliczyć sprawność cyklu złożonego z izobary o malejącej objętości i izochory o rosnącym ciśnieniu połączonych na wykresie pV prostym odcinkiem. Autorzy nadesłanych rozwiązań nie uwzględnili, że ciepło pobierane jest tylko na części tego odcinka, a na pozostałej części oddawane.
Zadanie 754 (\(WT = 3{,}51\)) z elektrostatyki poprawnie i elegancko rozwiązał Krzysztof Magiera.
W zadaniu 750 (\(WT = 3{,}14\)) należało znaleźć kąt odbicia od podłoża spadającego, rozkręconego do danej prędkości koła rowerowego i uwzględnić przypadki odbicia przed i po zakończeniu poślizgu. Najlepsze rozwiązanie z błędem rachunkowym, który spowodował jednak, że rozwiązania dla dwóch przypadków się nie ,,zszywały”, przysłał Marian Łupieżowiec.
Zadanie 743 (\(WT = 3{,}1\)) dotyczyło obwodu ze źródłem prądu stałego połączonego szeregowo z dwoma kondensatorami. Do jednego z kondensatorów dołączono równoległe, połączone w szereg cewkę i diodę. Poprawnie na wszystkie pytania odpowiedział Ryszard Baniewicz, a z błędem rachunkowym Jan Zarzycki.
W zadaniu 759 (\(WT = 2{,}95\)) metalowe, okrągłe, równoległe płytki, których środki połączone były przewodnikiem, obracały się w przeciwnych kierunkach wokół wspólnej osi w prostopadłym do płytek polu magnetycznym. Należało znaleźć napięcia między punktami płytek znajdującymi się naprzeciw siebie. Zadanie rozwiązał bezbłędnie Konrad Kapcia, autorzy pozostałych rozwiązań nie uwzględniali siły elektrycznej działającej obok siły Lorentza na elektrony w płytce.
W zadaniu 742 (\(WT = 2{,}91\)) drewniana kulka przymocowana była za pomocą nici do dna cylindrycznego naczynia z wodą, w znanej odległości od jego środka. Pytanie było: do jakiej prędkości kątowej należało rozkręcić naczynie, aby nić odchyliła się od pionu o zadany kąt? Bezbłędne rozwiązania nadesłali Sławomir Buć i Paweł Perkowski. W innych, co było zaskoczeniem, pojawiło się nieprawdziwe założenie, że siła Archimedesa spowodowana ciśnieniem wody działa pionowo do góry, a nić odchyla się na zewnątrz. Tymczasem w obracającym się naczyniu siła odśrodkowa działająca na drewnianą kulkę jest mniejsza niż składowa siły Archimedesa w kierunku poziomym i warunek równowagi zapewnia działająca na zewnątrz siła naprężenia nici, zatem nić odchyla się do środka naczynia.
Żadne z wymienionych dotychczas nazwisk nie powtórzyło się, co świadczy o tym, że poziom w omawianym roku był dość wyrównany.
W zadaniu 753 (\(WT = 2{,}73\)) z optyki światło wychodzące z przedmiotu przechodziło przez soczewkę, odbijało się od ustawionego pod kątem \(\pi /4\) do jej osi optycznej zwierciadła płaskiego, a następnie wpadało do naczynia z warstwą wody. Należało znaleźć odległość tego naczynia od osi optycznej, aby ostry obraz powstał na dnie. Rozwiązania ocenione na jedynkę, podobne do ,,firmowego”, przysłali Konrad Kapcia, Paweł Perkowski i Tomasz Wietecha. Autorem również poprawnego rozwiązania, które oceniłam subiektywnie jako odrobinę mniej eleganckie, był Ryszard Baniewicz. Spodobał mi się pomysł Andrzeja Nowogrodzkiego, który porównywał drogi optyczne przebyte przez promienie w wodzie i powietrzu, ale niestety nie doprowadził go do pomyślnego końca.
Pytania w niektórych zadaniach były tak dobrane, żeby można było na nie odpowiedzieć, stosując narzędzia elementarne. Uczestnicy ligi zdecydowanie preferowali jednak bardziej zaawansowane metody matematyczne, co często pozwalało uogólnić rozwiązania, ale jednocześnie bardzo je wydłużało.
W zadaniu 760 (\(WT = 2{,}6\)) ze statyki sznurek przyczepiony był dwoma końcami do sufitu i znana była odległość środka sznurka od sufitu. Należało znaleźć naprężenie sznurka w najniższym punkcie i w połowie odległości od sufitu. Zadanie rozwiązali poprawnie R. Baniewicz, K. Kapcia, P. Perkowski i T. Wietecha, ale ku mojemu lekkiemu rozczarowaniu powołali się na gotowe wzory opisujące krzywą łańcuchową.
Zadanie 744 (\(WT = 2{,}7\)) dotyczyło pocisku balistycznego. Pytanie było: z jaką najmniejszą prędkością i pod jakim kątem należy go wystrzelić z bieguna, aby poruszając się pod wpływem siły ciężkości, trafił w punkt na równiku? S. Buć rozwiązał zadanie w podobny sposób jak proponowany, wykorzystując wiedzę, że pocisk porusza się po fragmencie elipsy. T. Wietecha rozwiązał równanie ruchu tego pocisku we współrzędnych biegunowych.
Najwięcej rozwiązań ocenionych na maksymalną liczbę punktów przysłali Konrad Kapcia (11), Paweł Perkowski (10) i Tomasz Wietecha (8).
Barierę 44 punktów przekroczyli: P. Perkowski po raz piąty, J. Zambrzycki po raz czwarty i S. Buć po raz pierwszy.
Zadania z matematyki nr 875, 876
Termin nadsyłania rozwiązań: 30 IV 2024
Redaguje Marcin E. KUCZMA
875. Dany jest ciąg \((x_1,\ldots,x_N)\) o wyrazach \({x_i\in\{0,1\}}\) (\(N\) jest ustaloną liczbą nieparzystą). Niech \({a_k=\sum_{i<k}x_i},\) \({b_k=\sum_{i>k}(1-x_i)},\) \({c_k=a_k+b_k}\) (dla \({k=1,\ldots,N}\)). Wiadomo, że dokładnie jedna liczba \(z\) występuje w ciągu \((c_1,\ldots,c_N)\) nieparzyście wiele razy. Dla ustalonego \(N\) wyznaczyć wszystkie możliwe wartości \(z.\)
876. Wykazać, że dla liczb \({x,y,z\ge0}\) o sumie 3 zachodzi nierówność: \[{x\over y^2+y+1}+{y\over z^2+z+1}+{z\over x^2+x+1}\ge1.\]
Zadanie 876 zaproponował pan Witold Bednarek z Łodzi.
Lista uczestników ligi zadaniowej
Klub 44 M
po zakończeniu sezonu (roku szkolnego) 2022/23
Radosław Kujawa 43,57 Paweł Najman 8–43,16 Adam Woryna 3–40,91 Marek Spychała 4–40,20 Janusz Fiett 3–39,62 Jerzy Cisło 16–37,70 Paweł Kubit 7–36,11 Szymon Tur 35,35 Piotr Kumor 15–35,26 Janusz Olszewski 23–33,61 Łukasz Merta 2–31,48 Piotr Wiśniewski 29,69 Jędrzej Biedrzycki 29,54 Marian Łupieżowiec 1–28,80 Witold Bednarek 9–28,13 Krzysztof Kamiński 3–27,16 Janusz Wojtal 26,30 Roksana Słowik 2–23,94 Maciej Mostowski 1–22,90 Krzysztof Zygan 1–21,89 Marcin Małogrosz 4–20,62 Andrzej Kurach 3–20,51 Michał Kieza 4–20,46 Grzegorz Wiączkowski 19,95 Karol Matuszewski 1–19,74 Stanisław Bednarek 3–17,73 Błażej Żmija 2–17,31 Patryk Jaśniewski 1–16,62 Piotr Łaba 14,50 Tomasz Wietecha 14–13,65 Legenda (przykładowo): stan konta 9–28,13 oznacza, że uczestnik już dziewięciokrotnie zdobył 44 punkty, a w kolejnej (dziesiątej) rundzie ma 28,13 punktu.
Zestawienie obejmuje wszystkich uczestników ligi, którzy spełniają następujące dwa warunki:
– stan ich konta (w aktualnie wykonywanej rundzie) wynosi co najmniej 13 punktów;
– przysłali rozwiązanie co najmniej jednego zadania z rocznika 2021, 2022 lub 2023.Nie drukujemy więc nazwisk tych uczestników, którzy rozstali się z ligą trzy lata temu (lub dawniej); oczywiście jeśli ktoś zdecyduje się wrócić do naszych matematycznych łamigłówek, nazwisko tej osoby automatycznie wróci na listę. Serdecznie zapraszamy!
Rozwiązania zadań z numeru 10/2023
Przypominamy treść zadań:
867. Wyznaczyć wszystkie liczby naturalne \({n\ge3},\) dla których istnieje \(n\)-elementowy zbiór różnych liczb całkowitych \(M\) o następującej własności: w każdym trójelementowym podzbiorze zbioru \(M\) są dwie liczby, których suma jest potęgą liczby 2 o wykładniku całkowitym nieujemnym.
Przykład zbioru sześcioelementowego: \(\{-1,3,5,-2,6,10\}.\) Dowolny jego trójelementowy podzbiór ma dwa elementy leżące w trójce \(\{-1,3,5\}\) lub w trójce \(\{-2,6,10\}\); a każda z nich ma wszystkie dwu-sumy postaci \(2^k.\)
Niech teraz \(M\) będzie zbiorem \(n\)-elementowym; \({n\ge7}.\) Jeśli ma on trójelementowy podzbiór złożony z liczb niedodatnich, to w nim żadna para nie sumuje się do potęgi dwójki. Zajmijmy się więc przypadkiem, gdy w zbiorze \(M\) jest co najmniej pięć liczb dodatnich. Niech \(z\) będzie największą z nich. Co najwyżej jedna suma postaci \({x+z}\) (gdzie \({0<x<z},\) \({x\in{M}}\)) może być potęgą dwójki – gdyby bowiem były dwie takie sumy \({x+z=2^j},\) \({y+z=2^k}\) (\({0<x<y<z},\) więc \({j<k}\)), mielibyśmy \({y+z=2^{k-j}(x+z)>2z},\) wbrew temu, że \({y<z}.\)
Istnieją zatem w zbiorze \(M\) co najmniej trzy liczby dodatnie \({a,b,c<z},\) z których żadna nie daje w sumie z liczbą \(z\) wyniku postaci \(2^m.\) Niech \(c\) będzie największą z nich. Rozumowanie, analogiczne do przeprowadzonego powyżej, pokazuje, że co najmniej jedna z sum \({a+c},\) \({b+c}\) (przyjmijmy, że \({a+c}\)) nie jest potęgą dwójki. Tak więc trójelementowy zbiór \(\{a,c,z\}\) nie zawiera pary z sumą: potęga dwójki.
Stąd odpowiedź: liczby \(n\) o postulowanej własności to 3, 4, 5, 6.
868. Ciąg nieskończony \(a_1,a_2,\ldots\) jest dany wzorami: \({a_1=1},\) \[a_{n+1}=1+{1\over a_1}+{1\over a_2}+\ldots+{1\over a_n}\ \ \ \ \hbox{dla}\;n\ge1.\] Wykazać istnienie i znaleźć wartość granicy \(\displaystyle{\lim_{n\to\infty}\bigl(a_n-\sqrt{2n}\,\bigr)}.\)
Podana rekurencja daje się zapisać prościej: \({a_{k+1}=a_k+{1\over a_k}}\) (dla \({k\ge1}\)). Stąd \({a_{k+1}^2=a_k^2+2+{1\over a_k^2}}.\) Ustalmy \({n\ge2}.\) Sumowanie po \({k=1,\ldots,n{-}1}\) daje po redukcji zależność: \[a_n^2=2n-1+\sum_{k=1}^{n-1}{1\over a_k^2}=2n+\sum_{k=2}^{n-1}{1\over a_k^2} \ \ \ (*)\] (bo \({a_1=1}\)). Stąd widać, że \({a_n^2\ge2n}\) (dla \({n\ge2}\)). Zamieniamy literkę \(n\) na \(k\) i przepisujemy tę nierówność jako \({{1\over a_k^2}\le{1\over 2k}}\) (dla \({k\ge2}\)). Wstawiamy to ponownie do wzoru \((*)\) i dostajemy oszacowanie: \[a_n^2\le2n+\sum_{k=2}^{n-1}{1\over 2k}<2n+{1\over 2}\,H_n\] (zwykłe oznaczenie: \({H_n=1+{1\over 2}+\ldots+{1\over n}}\)). Tak więc (dla \({n\ge2}\)): \[0\le a_n-\sqrt{2n}={a_n^2-2n\over a_n+\sqrt{2n}}<{{{1\over 2}}\,H_n\over 2\sqrt{2n}}\,.\] Iloraz po prawej stronie dąży do zera, gdy \({n\to\infty}\) (znana asymptotyka: \({H_n\sim\ln{n}}\)). Stąd, ostatecznie, \(\displaystyle{\lim\bigl(a_n-\sqrt{2n}\,\bigr)=0}.\)
Weterani Klubu 44 M
(w kolejności uzyskiwania statusu weterana):
J. Janowicz (8), P. Kamiński (5), M. Gałecki (5), J. Uryga (4), A. Pawłowski (4), D. Sowizdrzał, T. Rawlik (6), M. Mazur, A. Bonk, K. Serbin, J. Ciach (5), M. Prauza (4), P. Kumor (15), P. Gadziński (7), K. Jedziniak, J. Olszewski (23), L. Skrzypek (4), H. Kornacki, T. Wietecha (14), T. Józefczyk, J. Witkowski (5), W. Bednorz, B. Dyda (5), M. Peczarski, M. Adamaszek (8), P. Kubit (7), J. Cisło (16), W. Bednarek (9), D. Kurpiel, P. Najman (8), M. Kieza (4), M. Kasperski (5), K. Dorobisz, A. Woryna, T. Tkocz, Z. Skalik (4), A. Dzedzej, M. Miodek, M. Małogrosz (4), K. Kamiński, J. Fiett, M. Spychała (4), A. Kurach, S. Bednarek, M. Pater
(jeśli uczestnik przekroczył barierę 44 punktów więcej niż trzy razy, sygnalizuje to liczba w nawiasie).
Pozostali członkowie Klubu 44 M
(alfabetycznie):
,,dwukrotni”: Z. Bartold, A. Czornik, A. Daniluk, Z. Galias, Ł. Garncarek, J. Garnek, A. Idzik, P. Jędrzejewicz, G. Karpowicz, H. Kasprzak, T. Komorowski, Z. Koza, J. Łazuka, J. Małopolski, Ł. Merta, J. Mikuta, E. Orzechowski, R. Pagacz, K. Patkowski, K. Pióro, F. S. Sikorski, J. Siwy, R. Słowik, S. Solecki, T. Warszawski, G. Zakrzewski, B. Żmija;
,,jednokrotni”: R. M. Ayoush, T. Biegański, W. Boratyński, P. Burdzy, T. Choczewski, M. Czerniakowska, P. Duch, P. Figurny, M. Fiszer, L. Gasiński, A. Gluza, T. Grzesiak, K. Hryniewiecki, K. Jachacy, M. Jastrzębski, P. Jaśniewski, A. Jóźwik, J. Klisowski, J. Kraszewski, A. Krzysztofowicz, T. Kulpa, A. Langer, R. Latała, P. Lipiński, P. Lizak, P. Łabędzki, M. Łupieżowiec, W. Maciak, J. Mańdziuk, B. Marczak, M. Marczak, M. Matlęga, K. Matuszewski, K. Maziarz, R. Mazurek, H. Mikołajczak, M. Mikucki, J. Milczarek, R. Mitraszewski, K. Morawski, M. Mostowski, W. Nadara, W. Olszewski, R. Pikuła, B. Piotrowska, W. Pompe, N. Porwol, M. Roman, M. Rotkiewicz, A. Ruszel, Z. Sewartowski, A. Smolczyk, P. Sobczak, Z. Surduka, T. Szymczyk, W. Szymczyk, W. Tobiś, K. Trautman, P. Wach, J. Węgrecki, K. Witek, A. Wyrwa, M. Zając, Z. Zaus, K. Zawisławski, K. Zygan, P. Żmijewski.
Podsumowanie ligi zadaniowej Klubu 44 M w roku szkolnym 2022/2023
Pora na doroczne omówienie. Jak co roku, przyjrzymy się wybranym zadaniom z minionego sezonu, więc głównie tym, które okazały się trudniejsze – wysoki współczynnik trudności (\(WT\)) i/lub niewielka liczba poprawnych rozwiązań (\(LPR\)). Przedstawiamy ciekawe pomysły rozwiązań oraz komentarze uczestników. Niektóre ich fragmenty umieszczamy w e-wydaniu (w zakładce ,,Załącznik do elektronicznego omówienia ligi matematycznej”).
Warto zwrócić uwagę na powtarzającą się sytuację, gdzie, nietypowo – przy ,,zasadniczo” właściwej koncepcji – uwadze rozwiązującego umyka jakiś niuans; dopracowanie rozwiązania często jest całkiem proste – a niekiedy wcale nie ,,całkiem”…
\(*\ \ \ *\ \ \ *\)
Zadanie 845. [\({x_i,y_j\ge 0}\) (\({i,j=1,\ldots,n}\)) \(\Rightarrow\) \({\bigl(\sum_{i\ne{j}}x_iy_j\bigr)^2\ge \bigl(\sum_{i\ne{j}}x_ix_j\bigr)\bigl(\sum_{i\ne{j}}y_iy_j\bigr)}\)] \(({WT=2{,}41};\) \({LPR=11}).\) W oznaczeniach z rozwiązania firmowego (\({S_x=\sum{x_i}},\) \({S_y=\sum{y_i}},\) \({Q_x=\sum{x_i^2}},\) \({Q_y=\sum{y_i}^2},\) \({T=\sum{x_iy_i}}\)) należy wykazać, że \({(S_xS_y-T)^2\ge(S_x^2-Q_x)(S_y^2-Q_y)}.\)
W kilku pracach zostało to zrobione prościej niż ,,firmowo”. Dla ilustracji – Witold Bednarek: rozwijamy kwadraty i grupujemy według potęg \(S_x\); daje to do wykazania (po odrzuceniu banalnego przypadku \({Q_y=0}\)) nierówność kwadratową względem \(S_x\): \[Q_yS_x^2-2TS_yS_x+(T^2+S_y^2Q_x-Q_xQ_y)\ge0.\] Wystarczy, że wyróżnik \(\Delta\) tego trójmianu będzie niedodatni; a tak jest, bowiem \[\Delta=4(T^2-Q_xQ_y)(S_y^2-Q_y)=4({\rm{czynnik}}\le0)({\rm{czynnik}}\ge0).\] Równie prosto (i dość podobnie): Michał Adamaszek, Piotr Kumor oraz Janusz Olszewski, który ponadto pokazał jeszcze kilka sposobów (\(\to\) e-wydanie).
Zadanie 847. [\({f\colon\,{\mathbb{R}}\to{\mathbb{R}}}\) ciągła;
\({\forall{a,b}\,(a{<}b)\,
\exists\,u,v\colon\,a{\le}u{<}v{\le}b\,
\forall\,x\in[a,b]\colon\,
f(u){\le}f(x){\le}f(b)}\) \(\Rightarrow\) \(f\) niemalejąca] \(({WT=2{,}07};\) \({LPR=12}).\)
Piotr Kumor zwrócił uwagę, że w założeniu można odrzucić istnienie jednej z liczb \(u,v,\) na przykład \(u,\) wymagając jedynie, by \({f(a)\le{f(v)}}.\) Zadanie niezbyt trudne; było wszelako kilka prób dowodu nie wprost opartych na domniemaniu, że jeśli funkcja ciągła nie jest niemalejąca, to na pewnym podprzedziale jest malejąca. Tak jednak być nie musi; kontrprzykłady można znaleźć w wielu miejscach; tu zacytujemy
http://math.stackexchange.com/questions/42326.
Zadanie 849. [\({4^x+4^y+1=z^4}\); \({x,y,z\in{\mathbb{N}}}\) \(\Rightarrow\) \({x,y,z=\,?}\,\)] \(({WT=2,53};\) \({LPR=8}).\) Ogólniejsze warianty tego równania znajdują się w literaturze. László Szalay w pracy z roku 2002 podał pełne rozwiązanie (w liczbach naturalnych) równania \({2^a+2^b+1=c^2},\) na co zwrócił uwagę Michał Adamaszek – a także Piotr Kumor, który (jak niejednokrotnie bywało) przysłał obszerny esej (\(\to\) e-wydanie) zawierający omówienie wzmiankowanej pracy oraz dwóch innych prac, wraz z potrzebnymi odsyłaczami (i garścią własnych refleksji).
Ponadto dobre rozwiązania przysłali: W. Bednarek, J. Cisło, K. Kamiński, J. Olszewski (dwa sposoby), M. Pater, P. Wiśniewski.
Zadanie 850. [\(\triangle{ABC}\) ostrokątny; \(M\) – środek \(BC\); \(P\) na odcinku \(AM\); \({BP\cap{AC}=D}\); \({CP\cap{AB}=E}\); \({({\rm{okr}}ABC)=\Omega}\); \({BP\cap\Omega=\{B,X\}}\); \({CP\cap\Omega=\{C,Y\}}\) \(\Rightarrow\) \({\exists\,T}\) na odcinku \(AM\colon\,\) \({T\ne{A}}\); \({T\in({\rm{okr}}AXD)\cap({\rm{okr}}AYE)}\)] \(({WT=2{,}92};\) \({LPR=3~(8~?)}).\) Zadanie zrobili: M. Adamaszek, S. Tur, M. Pater, J. Olszewski, A. Kurach, T. Wietecha, J. Cisło, M. Spychała. Wszyscy bezbłędnie pokazali, że okręgi \(AXD\) i \(AYE\) przecinają się (poza \(A\)) w punkcie leżącym na prostej \(AM\); ale tylko trzej autorzy, wymienieni w pierwszej kolejności, pokazali, że leży on na odcinku \(AM\); w pozostałych pracach ten aspekt tezy albo został zignorowany, albo odczytany z rysunku, który ,,wygląda, jak wygląda” – bez wyraźnego uzasadnienia konfiguracji.
Zadanie 851. [Marcin sprasza gości… Graf prosty \((V,E)\); \({|V|=50}\); \({T=\bigl\{\,\{i,j,k\}\subset{V}\colon\, {i{\ne}j{\ne}k{\ne}i}\;|\{ij,ik,jk\}\cap{E}|\in\{1,2\}\bigr\}}\); \({|T|\ge{3\over 4}{50\choose 3}}\); \({\min|E|=\,?}\,\)] \(({WT=2{,}97};\) \({LPR=5~(7~?)}).\) Wynik: 525. Dobre rozwiązania (niewiele się różniące od firmowego): nierówność Cauchy’ego–Schwarza lub między średnimi plus konstrukcja grafu realizującego równość: M. Adamaszek, J. Cisło, J. Olszewski, M. Pater; oraz P. Wiśniewski z banalną konstrukcją grafu 21-regularnego (bo taki okazuje się optymalny): 50 punktów na okręgu, połączenia między punktami leżącymi w odległości \({{}\ge15/50}\) (długości okręgu).
W dwóch innych pracach powtarza się rozumowanie: dorysowujemy krawędzie kolejno, po jednej, tak by w każdym kroku maksymalizować liczbę nowo powstałych dobrych trójek \(T\) (stop, gdy osiągniemy \({{3\over 4}{50\choose3}}\)). Tu jednak znacząca usterka logiczna: skąd wiadomo, czy jakaś inna strategia, rezygnująca z optymalizcji na każdym kroku, nie okaże się globalnie bardziej skuteczna?
Zadanie 856. [Czy istnieje ciąg \((a_i)_{i=1}^\infty\) taki, że zarówno on, jak i ciąg \((d_i)_{i=1}^\infty,\) gdzie \({d_i=|a_i{-}a_{i+1}|},\) jest permutacją zbioru \({{\mathbb{N}}=\{1,2,3,\ldots\}}\,\)?] \(({WT=2{,}20};\) \({LPR=12}).\) Jest wiele takich ciągów. Konstrukcja indukcyjna: w każdym kolejnym kroku ciąg jest przedłużany o kilka wyrazów; w rozwiązaniu firmowym – stale o trzy, według jednolitej procedury. Jednak zgrabniejsze były rozwiązania, w których procedura zmieniała się, często w zależności od bieżącego stanu (w stylu: if…then…else…). W e-wydaniu zamieszczamy trzy takie prace (M. Adamaszek, J. Cisło, J. Fiett), gdzie metoda była prosta, a opis klarowny (choć w najkrótszej z nich Czytelnik musi sobie coś w uzasadnieniu dopowiedzieć).
Jeszcze dwie prace prezentujemy w e-wydaniu: Janusz Olszewski wskazał metodę, przy której każdy z ciągów \((a_i),\) \((d_i)\) oraz \((e_i),\) gdzie \({e_i=|d_i-d_{i+1}|},\) stanowi permutację zbioru \({\mathbb{N}}\); i przypuszcza, że metodę można tak usprawnić, by permutację \({\mathbb{N}}\) stanowiły także ciągi o wyrazach \({f_i=|e_i-e_{i+1}|},\) \({g_i=|f_i-f_{i+1}|}\) itd., przez cały (nieskończony) alfabet. O tym, że tak jest w istocie, przekonuje Piotr Kumor, podając stosowne odsyłacze do literatury.
Zadanie 858. [Zbiór \({Z=\{A,B,C,D,E\}}\) w przestrzeni: \({AB=BC=CA=DE=1}\); \({(\triangle{ABC})\cap({\rm{odcinek}}DE)\ne\emptyset}\) \(\Rightarrow\) \({\exists{X\in{Z}}\,\forall\,{Y\in{Z}}\colon\;XY\le 1}\)] \(({WT=3{,}60};\) \({LPR=1}).\) Najtrudniejsze w omawianym sezonie. Autor: Michał Adamaszek. Dobra praca: Janusz Olszewski – zamieszczona w e-wydaniu (trochę za długa, by ją skrótowo tu w druku przedstawić). To jedyne poprawne rozwiązanie, przy tym różne od firmowego (podanego przez Autora i niezależnie – w nieco innym języku – przez redaktora ligi). Był jeszcze jeden ciekawy dowód, niestety przy dodatkowym (upraszczającym) założeniu, że odcinek \(DE\) przecina brzeg trójkąta \(ABC.\)
Zadanie 861. [\(\triangle{ABC}\): \({AC=BC}\); \({D\in({\rm{odc}}AC)},\) \({E\in({\rm{odc}}BD)}\); \({2AD=BD},\) \({2BE=AD}\) \(\Rightarrow\) \({\measuredangle{CDE}=2\measuredangle{CED}}\)] \(({WT=1{,}93}\); \({LPR=8}).\) Różne metody; wszystkie przebija urodą rozwiązanie, które pokazał Janusz Olszewski; niech (jak w firmówce) \({BE=a},\) \({CD=b}\); okrąg o środku \(C\) i promieniu \(b\) przecina proste \(BD\) oraz \(BC\) odpowiednio w punktach \(D,U\) oraz \(V,W,\) przy czym \({BV<BW}.\) Wtedy \({BD\cdot{BU}=BV\cdot{BW}},\) czyli \({4a\cdot{BU}=2a\cdot(2a+2b)}\); stąd \({BU=a+b},\) więc \({EU=b}\); przy konfiguracji jak na rysunku (\({EU\le{ED}}\)) dostajemy tezę: \({\measuredangle{CDE}=\measuredangle{CUD}=2\cdot\measuredangle{CED}}\) (!). (Końcówka wymaga niewielkiej modyfikacji, gdy \({EU>ED}\); ale Autor dostarczył jeszcze dwa inne rozwiązania, mniej zwięzłe i efektowne, za to działające bez retuszu przy każdej konfiguracji).
Zadanie 862. [Graf skierowany, skończony; krawędzie w \(m\) kolorach; każdy wierzchołek ma stopień wychodzący \({{}>m}\) \(\Rightarrow\) z każdego wierzchołka wychodzi nieskończenie wiele nieskończonych ścieżek o identycznej sekwencji kolorów] \(({WT=2{,}64};\) \({LPR=4}).\) M. Adamaszek, S. Bednarek, J. Olszewski, K. Zygan przysłali dobre rozwiązania – we wszystkich istota rozumowania jest podobna jak w rozwiązaniu firmowym. Ponadto w dwóch pracach pojawia się dowód (poprawny), że dla każdej liczby naturalnej \(d\) można utworzyć zbiór identycznie pokolorowanych ścieżek długości \(d\) (wychodzących z ustalonego wierzchołka), przy czym moc tego zbioru rośnie, gdy \(d\) rośnie. To jednak jeszcze nie teza zadania (,,dowolnie wiele dowolnie długich” to nie to samo co ,,nieskończenie wiele nieskończenie długich”). Wypełnienie tej luki nie jest banalne.
Zadanie 863. [Liczba pierwsza \({p>2}\); \({\forall\,k\in\{1,\ldots,p{-}1\}\colon\;p+4k^2}\) – pierwsza; \({p=\,?}\)] \(({WT=2{,}33};\) \({LPR=9}).\) Styl przekombinowanego rozwiązania firmowego udzielił się (na szczęście) niewielu uczestnikom. Typową metodą było badanie serii przypadków, sterowanych resztami z dzielenia \(p\) przez niskie potęgi dwójki. Jako wzorzec niech posłuży rozumowanie, które przeprowadzili Jerzy Cisło i Krzysztof Kamiński: liczba \(p\) zapisuje się w dokładnie jednej z postaci \({4k+1},\) \({8k+3},\) \({16k+7},\) \({16k+15}\); wartość wyrażenia \({p+4k^2}\) wynosi wówczas odpowiednio \({(2k+1)^2},\) \({(2k+1)(2k+3)},\) \({(2k+1)(2k+7)},\) \({(2k+3)(2k+5)},\) co może być liczbą pierwszą jedynie przy \({k=0}\); zatem \(p\) (liczba pierwsza) może być równa jedynie 3 lub 7; i łatwo sprawdzić, że 3 i 7 spełniają wymagane warunki.
Janusz Olszewski zauważył zbędność założenia, że liczba \(p\) jest pierwsza (\(\to\) e-wydanie; tam również zamieszczamy interesujący komentarz, jakim opatrzył swoją pracę Michał Adamaszek).