Klub 44

Zadania z matematyki nr 899, 900

Termin nadsyłania rozwiązań: 30 VI 2025

Redaguje Marcin E. KUCZMA

899. Niech \({g\colon\mathbb{Z^2}\to\mathbb{R}}\) będzie dowolną funkcją ( \(\mathbb{Z}^{2}\)  jest zbiorem punktów kratowych, czyli uporządkowanych par liczb całkowitych). Określamy odległość punktów \({P,Q\in\mathbb{Z^2}},\) \({P=(x,y)},\) \({Q=(u,v)}\) wzorem \({d(P,Q)=\max(|x-u|,|y-v|)}.\) Dowieść, że istnieje nieskończenie wiele pięcioelementowych zbiorów punktów kratowych \((P_{0},P_{1},P_{2},P_{3},P_{4})\) takich, że (dla \({i=1,2,3,4}\) ):   \({d(P_0,P_i)=1},\)   \({g(P_0)\le{g(P_i)}}.\)

900. Wielomiany \(f_{1},f_{2},f_{3},f_{4}\) jednej zmiennej, o współczynnikach rzeczywistych, spełniają warunki: \[\begin{aligned} f_{1}(x)\le f_{2}(x)\le f_{3}(x)\le f_{4}(x)\ \ \ &\hbox{dla}\;x\in[0,1], \\ f_{2}(x)\le f_{4}(x)\le f_{1}(x)\le f_{3}(x)\ \ \ &\hbox{dla}\;x\in[-1,0]. \end{aligned}\] Wykazać, że \({f_1=f_2=f_3=f_4}.\)

Zadanie 900 zaproponował pan Michał Adamaszek z Kopenhagi.

Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
885 ( \(WT = 1{,}95\) ) i 886 ( \(WT = 1{,}42\) )
z numeru 9/2024

Mikołaj Pater		42,95
Witold Bednarek	Łódź	42,00
Tomasz Wietecha	Tarnów	41,98
Krzysztof Zygan	Lubin	39,38
Andrzej Daniluk	Warszawa	37,89
Andrzej Kurach	Ryjewo	36,18
Michał Warmuz	Żywiec	33,21
Marcin Kasperski	Warszawa	32,31
Jędrzej Biedrzycki		32,29
Krzysztof Kamiński	Pabianice	31,90
Grzegorz Wiączkowski		31,79
Marian Łupieżowiec	Gliwice	31,29

Korekta omyłki redakcyjnej: W rocznym zestawieniu listy uczestników ( Delta 2/2025) przy nazwisku Grzegorz Wiączkowski powinno być podane saldo 29,40.

Rozwiązania zadań z numeru 12/2024

891. Oznaczmy: \({\cos\bigl(2^n\varphi\bigr)=x_n}\) (więc \({|x_n|\le1}\) ). Ze wzoru na kosinus podwojenia wynika zależność rekurencyjna   \({x_{n+1}=2x_n^2-1}.\)  Badamy, dla jakich wartości początkowych  \(x_{0}\) spełniony jest warunek: wszystkie \({x_n\in[-1,0]}.\)

Niech \(y_{n}=x_{n}+\frac{1}{2}.\) Warunek zadania przybiera postać \(|y_{n}|\le\frac{1}{2},\) a wzór rekurencyjny – postać: \[y_{n+1}=-y_{n}(2-2y_{n})\ \ \ \ \hbox{dla}\;\;n=0,1,2,\ldots \tag{1}\] Skoro \(|y_{n}|\le\frac{1}{2},\) wyrażenie w nawiasie ma wartość  \({{}\ge1}\) ; a gdy \({y_n\le0},\) ma wartość  \({{}\ge2}.\) Zatem \[|y_{n+1}|\ge\begin{cases}|y_{n}|&\text{dla każdego~$n,$}\\ 2|y_{n}|&\text{gdy ${y_n\le0}.$}\\\end{cases} \tag{2}\] Ze wzoru (1) widać ponadto, że w każdej parze kolejnych wyrazów ciągu igreków jest liczba niedodatnia. Z własności (2) wynika teraz, że   \({|y_{n+2}|\ge2|y_n|}\)  dla wszystkich  \(n.\) Stąd przez indukcję   \({|y_{2n}|\ge2^n|y_0|}\) ;  a ponieważ \({|y_{2n}|\le\frac{1}{2}},\) musi być \({y_0=0}.\) To odpowiada wartości \({x_0=-\frac{1}{2}}\) (i wtedy wszystkie \({x_n=-\frac{1}{2}}\) ).

Wymagany warunek jest więc spełniony wtedy i tylko wtedy, gdy   \({x_n=\cos\varphi=-\frac{1}{2}},\)  czyli jedynie dla   \({\varphi=\pm\frac{2}{3}{\,}\pi+2m\pi}\)  ( \({m=0,\pm1,\pm2,\ldots}\) ).

892. Rozwiązanie Autora (Michał Adamaszek). Przyjmijmy, że zawodnik dostaje 1 punkt za wygraną i 0 za porażkę. Ustalmy  \(k\) ; niech \(S\) będzie zbiorem zawodników, którzy zakończyli turniej z  \(k\)  punktami; niech \({|S|=s}.\) Pomiędzy sobą rozegrali oni \({s\choose2}\) partii, więc wspólnie zdobyli co najmniej tyle właśnie punktów. Jednak z definicji  \(S\) wiemy, że zdobyli razem dokładnie \(ks\)  punktów. Stąd \({{s\choose2}\le{ks}},\) czyli \({s\le2k+1}.\)

Przypuśćmy teraz, że wszystkie mecze w turnieju zakończyły się odwrotnymi wynikami ( \({0\mapsto1},\) \({1\mapsto0}\) ). W tym nowym turnieju \(S\) jest zbiorem tych zawodników, którzy zdobyli dokładnie \({n-k-1}\) punktów, więc to samo rozumowanie daje wniosek, że \({{s\choose2}\le(n-k-1)s},\) czyli \({s\le2n-2k-1}.\) Zatem \[s\le\min\{2k+1,2n-2k-1\}.\] Pokażemy, że to oszacowanie jest osiągalne. W przypadku, gdy \({1\le2k+1\le{n}},\) niech \(S\) będzie dowolnym zbiorem zawodników o tej właśnie liczności. Łatwo ustawić mecze wewnątrz  \(S\) tak, aby każdy wygrał ich dokładnie  \(k\) (np.: każdy wygrywa z  \(k\) swoimi następnikami w dowolnym cyklicznym ustawieniu zbioru  \(S\) ). Zawodnikom spoza  \(S\) każemy wygrać wszystkie mecze przeciwko  \(S\) i dowolnie między sobą. Wtedy każdy zawodnik z  \(S\) zdobywa \(k\)  punktów, a każdy spoza  \(S\) co najmniej \({2k+1\ge{k+1}}\) punktów.

W przypadku, gdy \({n+1\le2k+1\le2n-1},\) niech \({j=n-1-k}.\) Wówczas \({1\le2j+1\le{n-1}},\) więc na mocy poprzedniej konstrukcji istnieje turniej, w którym dokładnie \({2j+1=2n-2k-1}\) zawodników zdobyło dokładnie \(j\) punktów. Odwracając wszystkie wyniki na przeciwne, otrzymujemy turniej, w którym dokładnie \({2n-2k-1}\) zawodników zdobyło dokładnie \({n-1-j=k}\) punktów.

Stąd odpowiedź: szukana maksymalna wartość  \(|S|\) wynosi   \({\min\{2k+1,2n-2k-1\}}.\)

Zadania z fizyki nr 796, 797

Termin nadsyłania rozwiązań: 30 VI 2025

Redaguje Elżbieta ZAWISTOWSKA

796. W obwodzie przedstawionym na rysunku 1 klucz zamknięto do położenia 1, a po ustaleniu się prądów bardzo szybko przełączono go do pozycji 2. Przyjmując, że cewki \(L_{1}\) i  \(L_{2}\) są idealne, wyznaczyć ilość ciepła, jaka wydzieli się na oporniku \(R\) po przełączeniu. Siła elektromotoryczna źródła wynosi \(\mathcal{E},\) jego opór wewnętrzny \(r.\)

797. W środku dna prostopadłościennej barki o długości \(a=80\)  m, szerokości \(b=10\)  m i wysokości \(c=5\)  m powstał otwór o średnicy \(d=1\)  cm. Ocenić czas, po którym barka zatonie, jeśli nie będzie odpompowywana z niej woda. Barka jest otwarta z góry, nie ma żadnego ładunku, początkowa wysokość burty nad poziomem wody wynosi \(h=3{,}75\)  m.

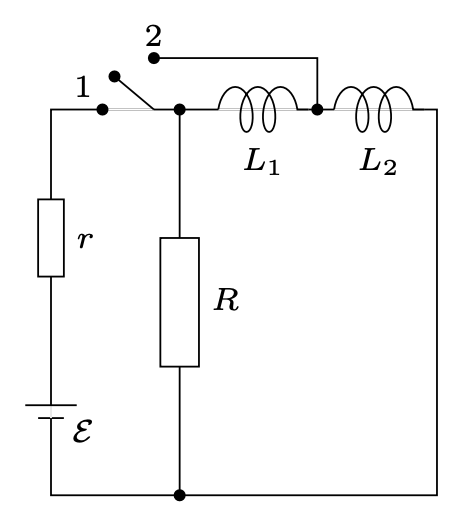
Rys. 1

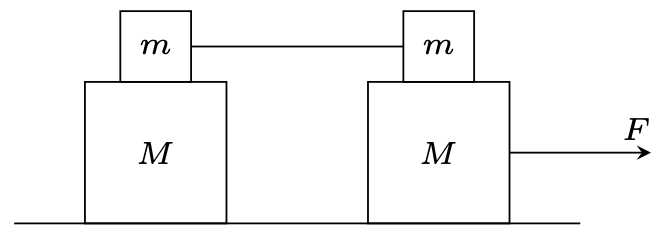
Rys. 2

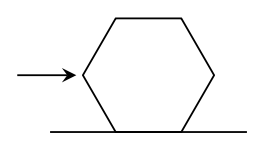
Rys. 3

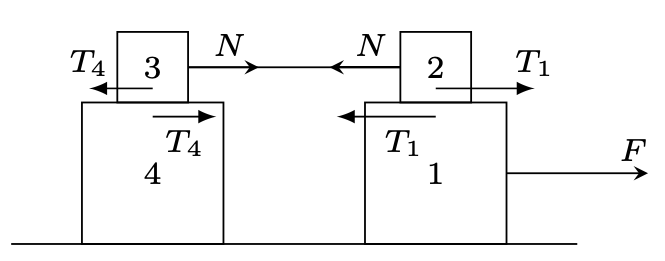
Rys. 4

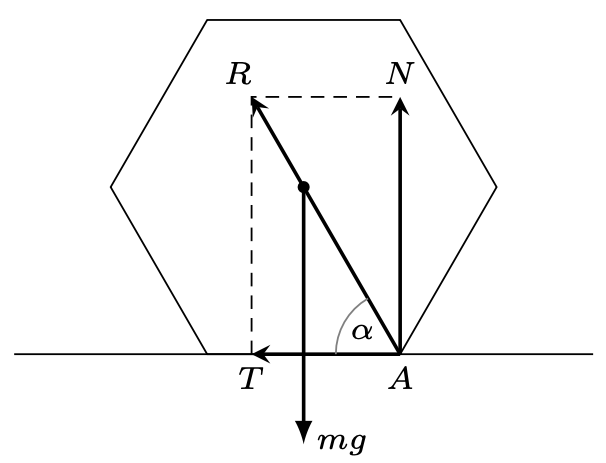
Rys. 5

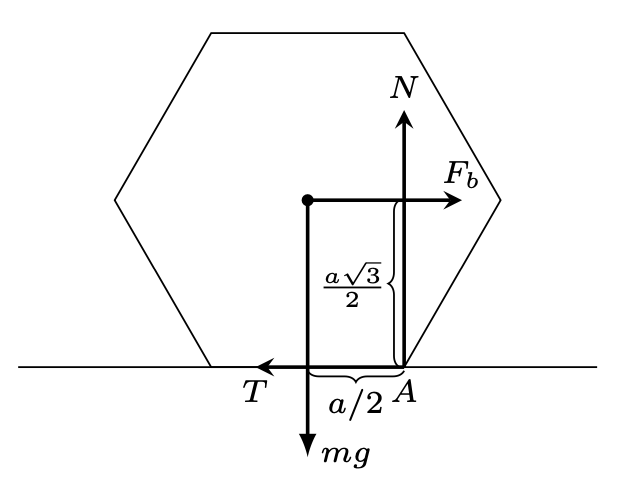
Rys. 6

788. Przyspieszenia klocków o masach \(m\) są takie same, bo łącząca je nić jest nierozciągliwa. Tarcie między klockami 3 i 4 (rys. 4) jest tarciem statycznym. Gdyby tak nie było i klocek 3 ślizgałby się po klocku 4, to siła tarcia między nimi \(T_{4}=\mu mg\) miałaby wartość mniejszą od siły naciągu nici \(N,\) a klocek 2 poruszałby się w lewo, co jest niemożliwe. Zatem przyspieszenia klocków 2, 3 i 4 są jednakowe. Oznaczmy je przez \(a_{2},\) a przyspieszenie klocka 1 przez \(a _{1}.\) Możliwe są dwa przypadki:

1) Nie ma poślizgu między klockami 1 i 2, układ porusza się jak jedno ciało: \[a_{1}=a_{2}=F/2(M+m) .\] Równanie ruchu klocka 1: \(Ma_{1}=F-T_{1}\) oraz warunek na brak poślizgu \(T_{1}\le\mu mg\) pozwala znaleźć warunek, jaki musi spełniać siła, aby zachodził przypadek pierwszy \(F\le 2\mu mg(M+m)/(M+2m).\)

2) Klocek 2 ślizga się po klocku 1:
Z równania ruchu klocka 1: \({a_{1}=(F-\mu mg)/M}.\)
Z równania ruchu układu klocków 2, 3, 4: \({a_{2}=\mu mg/(2m+M)}.\)
Przypadek drugi zachodzi, gdy siła spełnia warunek:
\({F> 2\mu mg(M+m)/(M+2m)}.\)

789. Zadanie możemy rozwiązać w układzie związanym z płaszczyzną albo z ołówkiem.

1) Układ inercjalny, związany z płaszczyzną: Na poruszający się ołówek działają ze strony płaszczyzny dwie siły: reakcji \(N\) i tarcia \(T.\) Ołówek nie może przemieszczać się w kierunku pionowym, więc siła reakcji jest równa sile ciężkości \(N=mg,\) siła tarcia \(T=\mu N=\mu mg.\) Rozważmy przypadek graniczny, gdy ołówek zaczyna się obracać wokół krawędzi \(A\) (rys. 5). Siły \(N\) i \(T\) są w tym momencie przyłożone do krawędzi \(A.\) Jeżeli wypadkowa tych sił \(R\) przechodzi poniżej osi ołówka, to jej moment względem osi wywołuje jego obrót. Warunek na brak obrotu ma postać: \[\tg\,\alpha=N/T\ge \tg\,60^{\circ},\ \ \ \mu\le1/\sqrt{3}.\] 2) Układ nieinercjalny, związany z ołówkiem: W tym układzie na ołówek działa dodatkowo siła bezwładności związana z przyspieszeniem nadanym przez siłę tarcia (rys. 6): \(F_{b}=ma=m\mu g.\) Ołówek obraca się wokół krawędzi \(A\) (chwilowa oś obrotu), jeżeli moment siły \(F_{b}\) względem \(A\) jest większy niż moment siły ciężkości: \[F_{b}a\sqrt{3}/2>mga/2.\] Otrzymujemy stąd taki sam jak poprzednio warunek na brak obrotu.