Zbiór Cantora przed Cantorem

Kontakt: gornicki59@gmail.com

Zbiory, które przedstawimy w niniejszym artykule, są jednymi z najbardziej niezwykłych. Pojawiają się w wielu fragmentach współczesnej matematyki. Dzięki nim lepiej rozumiemy skomplikowaną strukturę zbioru liczb rzeczywistych oraz płaszczyzny euklidesowej. Nie można wykluczyć, że zbiory te wciąż skrywają własności, które czekają na swoich odkrywców.

W 1875 roku irlandzki matematyk Henry Smith w pracy [1] wykazał, że ograniczona funkcja rzeczywista będzie całkowalna w sensie Riemanna „[nawet, gdy jej punkty nieciągłości] będą istnieć w nieskończonej liczbie w skończonym przedziale bez wypełnienia jakiejkolwiek części tego przedziału”. Ten opis może nam się wydać odrobinę dziwny, ale proszę zauważyć, że powstał on w czasach, gdy nie istniała ani teoria mnogości, ani topologia, ani teoria miary, jakie znamy dzisiaj. Mimo to jest on zadziwiająco zgodny z dzisiejszym stanem wiedzy, który podsumowuje poniższy wynik.

Henry J. S. Smith (1826–1883), matematyk irlandzki, od 1860 roku zajmował stanowisko Savilian Professor of Geometry w Oksfordzie

Twierdzenie 1. Funkcja ograniczona w przedziale domkniętym \(f:\Delta\rightarrow\mathbb{R},\) \(\Delta\subset\mathbb{R},\) jest całkowalna w sensie Riemanna w tym przedziale wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma miarę Lebesgue’a równą zero.

Trafność sformułowania Smitha jeszcze lepiej widać, gdy spojrzymy na podane przez niego przykłady zbioru punktów, które „mogą istnieć w nieskończonej liczbie w skończonym przedziale bez wypełnienia jakiejkolwiek części tego przedziału”.

Przykład 1 (Smith, 1875). Niech \(m\) będzie dowolną liczbą całkowitą większą od 2. Podzielmy przedział \([0,1]\) na \(m\) równych przedziałów i usuńmy ostatni segment („segment” to taki przedział, że to, co zostaje po jego usunięciu, jest zbiorem domkniętym). Każdy z pozostałych \(m-1\) przedziałów podzielmy na \(m\) równych przedziałów i usuńmy ostatni segment z każdego z nich (rys. 1).

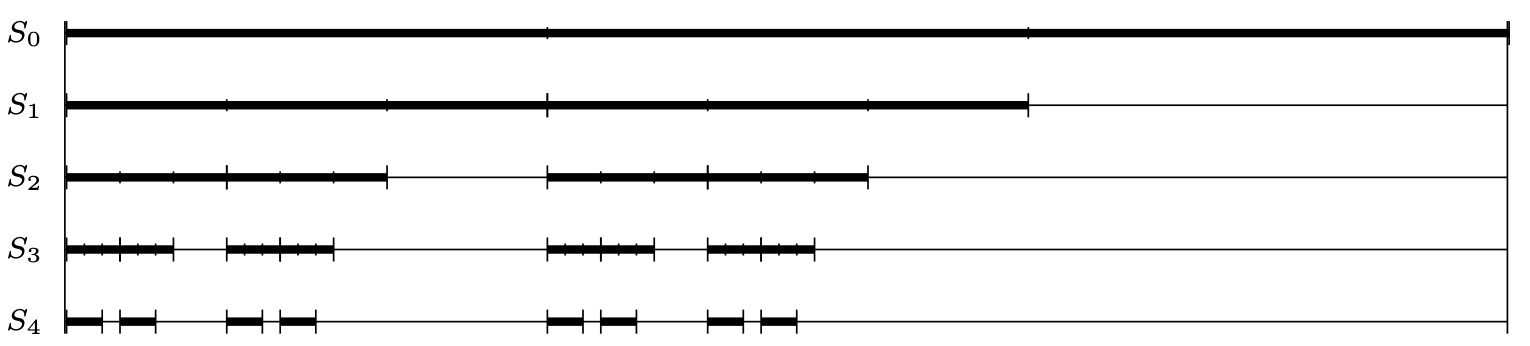
Rys. 1. Pierwsze etapy konstrukcji Smitha dla \(m=3\)

Jeżeli ta operacja będzie kontynuowana w nieskończoność, to otrzymamy domknięty zbiór \(\mathcal{S}\) o nieskończonej liczbie punktów, który nie wypełnia jakiejkolwiek części przedziału \([0,1].\) Łączna długość przedziałów, jakie pozostają po \(k\)-tym kroku konstrukcji, jest równa \(\big(\frac{m-1}{m}\big)^k\) i dąży do 0, gdy \(k\rightarrow\infty.\) Jednocześnie po \(k\) krokach konstrukcji długość usuniętych przedziałów jest równa \(1-\big(\frac{m-1}{m}\big)^k\) i dąży do 1, gdy \(k\rightarrow\infty.\) Zbiór \(\mathcal{S}\) nazywamy zbiorem Smitha.

Opisana konstrukcja Smitha to jeden z najwcześniejszych opublikowanych przykładów zbioru fraktalnego (samopodobnego) utworzonego rekurencyjnie!

Przejdźmy do omówienia tytułowego zbioru Cantora. W latach 1879–1884 matematyk niemiecki Georg Cantor badał topologiczne własności podzbiorów zbioru liczb rzeczywistych. W pracy [2], bez wskazania motywacji, podał przykład zbioru doskonałego i nigdziegęstego (to dla purystów, bo dalszy tekst nie wymaga znajomości tych pojęć).

Georg F. L. P. Cantor (1845–1918), matematyk niemiecki, profesor Uniwersytetu w Halle, twórca teorii mnogości

Przykład 2 (Cantor, 1883). Zbiór liczb postaci \[\mathcal{C}=\bigg\{x\in \mathbb{R}: x=\sum\limits_{i=1}^{\infty}\frac{c_i}{3^i},~~\hbox{gdzie}~~c_i\in\{0,2\}\bigg\},\] nazywamy zbiorem Cantora.

Zbiór Cantora tworzą zatem te liczby z przedziału \([0,1],\) które można zapisać w systemie trójkowym w postaci nieskończonego rozwinięcia przy użyciu tylko cyfr 0 lub 2. Należy przy tym pamiętać, że np. \(\frac{1}{3}\in \mathcal{C},\) bo \(\frac{1}{3}=(0{,}0222\dots )_3,\) a nie tylko \(\frac{1}{3}=(0{,}1)_3.\)

Zauważmy teraz, że w rozwinięciu \(x=(0{,}c_1c_2c_3\dots )_3,\)

Ponieważ prawdziwe są również implikacje odwrotne, więc zbiór Cantora możemy opisać geometrycznie: podzielmy przedział \([0,1]\) na trzy równe przedziały i usuńmy otwarty przedział środkowy. Każdy z pozostałych przedziałów podzielmy na trzy równe przedziały i z każdego takiego podziału usuńmy otwarty przedział środkowy. Jeżeli ta operacja będzie kontynuowana w nieskończoność, to otrzymamy w przedziale \([0,1]\) domknięty zbiór \(\mathcal{C}\) (rys. 2).

Myślimy tutaj o przypisaniu do liczby \((0{,}c_1c_2c_3\dots )_3\) granicy ciągu punktów przypisanych do liczb \((0{,}c_1)_3,\) \((0{,}c_1c_2)_3,\) \((0{,}c_1c_2c_3)_3\) itd., gdzie \(c_i\in \{0,2\}.\) W ten sposób wykorzystujemy fakt, że zbiór \(\mathcal{C}\) jest domknięty (jako zbiór doskonały).

Rys. 2. Pierwsze etapy geometrycznej konstrukcji zbioru Cantora

Podobnie jak w przykładzie 1, „długość” (w dzisiejszym języku: miara) zbioru Cantora jest równa 0.

Warto tutaj zaznaczyć, że nieznacznie modyfikując tę konstrukcję, możemy otrzymać zbiór o „długości” dodatniej: moglibyśmy na przykład w \(n\)-tym etapie konstrukcji zabierać ze środka każdego z aktualnych odcinków \(1/4^n\) jego długości. Otrzymany w ten sposób tzw. tłusty zbiór Cantora również „nie wypełnia jakiejkolwiek części przedziału”, nie spełnia jednak warunków Twierdzenia 1.

Porównując geometryczne konstrukcje zbioru Smitha (dla \(m=3\)) i zbioru Cantora, stwierdzamy, że \[\mathcal{S}=\bigg\{x\in \mathbb{R}: x=\sum\limits_{i=1}^{\infty}\frac{s_i}{3^i},~~\hbox{gdzie}~~s_i\in\{0,1\}\bigg\}~~\hbox{i}~~2\cdot\mathcal{S}=\mathcal{C}.\] Przy próbie rysowania przybliżeń zbioru Cantora widzimy jedynie wymierne końce wybranych przedziałów, których jest przeliczalnie wiele. Czy w zbiorze Cantora są inne liczby? Pokażemy (dwoma sposobami), że \(\frac{1}{4}\in \mathcal{C},\) choć nie jest końcem jakiegokolwiek przedziału z konstrukcji zbioru Cantora.

Sposób 1. Punkty \(x_1=\frac{1}{3},\) \(x_2=\frac{1}{3}-\frac{1}{9},\) \(x_3=\frac{1}{3}-\frac{1}{9}+\frac{1}{27}\) itd. są końcami przedziałów w konstrukcji zbioru Cantora, więc należą do zbioru \(\mathcal{C}.\) Jednocześnie \({\big(\frac{1}{3}\big)-\big(\frac{1}{3}\big)^2+\big(\frac{1}{3}\big)^3-\dots =\frac{1}{4}},\) więc \(\frac{1}{4}\in \mathcal{C},\) bo zbiór \(\mathcal{C}\) jest domknięty.

Sposób 2. Z definicji zbioru Cantora \(x=(0{,}020202\dots )_3\in \mathcal{C}.\) Ponieważ \[x=\frac{2}{3^2}+\frac{2}{3^4}+\frac{2}{3^6}+\dots =\frac{1}{3^2}\bigg(2+\bigg[\frac{2}{3^2}+\frac{2}{3^4}+\dots \bigg]\bigg)=\frac{1}{9}(2+x),\] więc \(x=\frac{1}{4}\in \mathcal{C}.\)

Podobnie do zbioru Cantora należy \(x=\sum\limits_{i=1}^{\infty}\frac{2}{3^{i!}},\) gdzie cyfra 2 występuje na miejscach \(i!\) po przecinku.

Twórca teorii mnogości wiedział, że zbiór \(\mathcal{M}\) wszystkich nieskończonych ciągów utworzonych z 0 lub 1 jest nieprzeliczalny, to znaczy nie da się utworzyć ciągu złożonego z wszystkich jego elementów.

Uzasadnienie jest łatwe. Załóżmy, że wszystkie elementy zbioru \(\mathcal{M}\) (będące ciągami) zostały ponumerowane liczbami naturalnymi (zostały ustawione w ciąg): \(M_1=\{m_i^1\}_{i=1}^{\infty},\) \(M_2=\{m_i^2\}_{i=1}^{\infty},\) \(\ldots\) Tworzymy nowy ciąg \(T=\{t_i\}_{i=1}^{\infty},\) który na \(i\)-tym miejscu różni się od ciągu \(M_i,\) przyjmując, że jeśli \(m_i^i=0,\) to \(t_i=1,\) a jeśli \(m_i^i=1,\) to \(t_i=0.\) Wtedy ciąg \(T\) \(\textrm{należy do}\) \(\mathcal{M}\) (bo zbudowany jest z 0 lub 1) i \(T\neq M_i\) dla każdego \(i=1,2,\dots\) Jest to sprzeczne z założeniem, że wszystkie elementy zbioru \(\mathcal{M}\) zostały ponumerowane liczbami naturalnymi, więc \(\mathcal{M}\) jest zbiorem nieprzeliczalnym.

Z poczynionych obserwacji wynikają następujące stwierdzenia.

Twierdzenie 2:

1. Zbiór Smitha ma tyle samo elementów co zbiór Cantora (równoliczność ustala funkcja mnożenia przez 2, czyli\[\mathcal{S}\ni (0{,}s_1s_2s_3\dots )_3\longmapsto (0{,}c_1c_2c_3\dots )_3\in \mathcal{C},\] gdzie \(s_i\in\{0,1\}\) i \(c_i=2s_i\) dla każdego \(i=1,2,\dots\));

2. Zbiór Smitha \((\)zbiór Cantora\()\) jest nieprzeliczalny.

Stwierdzenie (2) możemy wzmocnić, wykazując, że przekształcenie \[f\big((0{,}c_1c_2c_3\dots )_3\big)=\frac{1}{2}\sum\limits_{i=1}^{\infty}\frac{c_i}{2^i},~~\hbox{gdzie}~~c_i\in \{0,2\},\] odwzorowuje w sposób ciągły zbiór Cantora \(\mathcal{C}\) na przedział \([0,1].\) Wynika stąd, że zbiór \(\mathcal{C}\) ma nie mniej elementów niż jego obraz \(f(\mathcal{C})=[0,1].\) Ponieważ \(\mathcal{C}\subset [0,1],\) więc zbiór Cantora ma tyle samo elementów co przedział \([0,1].\)

Zatem większości liczb ze zbioru Cantora (zbioru Smitha) nie widzimy (!), choć jest ich tak dużo jak w całym przedziale \([0,1],\) i na dodatek wszystkie one mieszczą się na „odcinku” zerowej długości! Doprawdy niewiarygodne, jak matematyka potrafi zaskoczyć naszą intuicję i poruszyć wyobraźnię.

Jakby tego było mało, okazuje się, że ten „mały” zbiór może tworzyć zaskakująco duże zbiory, na przykład \[\mathcal{C}+\mathcal{C}=\{x+y:x,y\in \mathcal{C}\}=[0,2].\] Uzasadnienie jest następujące. Ponieważ \(\mathcal{C}\subset [0,1],\) więc oczywiście \(\mathcal{C}+\mathcal{C}\subset [0,2].\) Aby wykazać zawieranie przeciwne, ustalmy liczbę \(t\in [0,2].\) Musimy wskazać dwie liczby \(b,d\in \mathcal{C}\) takie, że \(b+d=t.\) Zauważmy, że jeśli \(C_1=[0,\frac{1}{3}]\cup [\frac{2}{3},1],\) to \(\{x+y:x,y\in C_1\}=[0,2].\) Powody wyjaśnia rysunek 3 (to jedna z możliwych realizacji).

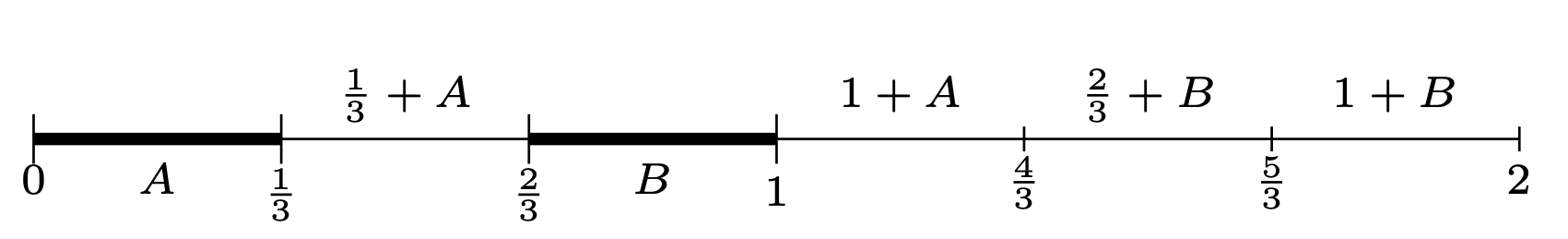
Rys. 3. Pierwsze etapy geometrycznej konstrukcji zbioru Cantora

Zatem istnieją liczby \(b_1,d_1\in C_1\) takie, że \(b_1+d_1=t.\) Analogicznie, jeśli \(C_2=[0,\frac{1}{9}]\cup [\frac{2}{9},\frac{1}{3}]\cup [\frac{2}{3},\frac{7}{9}]\cup [\frac{8}{9},1],\) to \(\{x+y:x,y\in C_2\}=[0,2].\) Istnieją więc liczby \(b_2,d_2\in C_2\) takie, że \(b_2+d_2=t.\) Kontynuując to postępowanie, możemy dla każdego \(i\) znaleźć liczby \(b_i,d_i\in C_i\) takie, że \(b_i+d_i=t.\) Oczywiście ciągi \(\{b_i\}_{i=1}^{\infty}, \{d_i\}_{i=1}^{\infty}\textrm{ zawierają się w } \mathcal{C},\) więc korzystając ze zwartości zbioru \(\mathcal{C},\) możemy uzasadnić istnienie podciągów \(\{b_{i_k}\}_{k=1}^{\infty},\) \(\{d_{i_k}\}_{k=1}^{\infty},\) które są zbieżne do liczb \(b,d\in \mathcal{C},\) odpowiednio. Ponieważ przechodzenie do granicy zachowuje operację dodawania, więc przechodząc z \(k\rightarrow\infty\) w równaniu \(b_{i_k}+d_{i_k}=t,\) otrzymujemy \(b+d=t.\) Zatem \([0,2]\subset \mathcal{C}+\mathcal{C},\) co kończy uzasadnienie. Podobnie moglibyśmy również pokazać, że \(\mathcal{C}-\mathcal{C}=[-1,1].\)

W przestrzeni euklidesowej \(\mathbb{R}\) zbiór \(A\) jest zwarty, gdy z każdego ciągu punktów zbioru \(A\) można wybrać podciąg zbieżny do elementu zbioru \(A\) (lub równoważnie, gdy zbiór \(A\) jest domknięty i ograniczony).

Obserwacje te mogą stanowić naturalny punkt wyjścia do rozważań nad miarą, kategorią i wymiarem zbiorów, i de facto stały się impulsem do rozwoju tych teorii na przełomie XIX i XX wieku. Problematyka ta jest jeszcze lepiej widoczna na tle uwagi Smitha z pracy [1]: „rozważając dla uproszczenia przypadek dwóch wymiarów, zauważmy, że [skończony przedział (czyli prostokąt) całkowania] może nie tylko zawierać punkty nieciągłości o skończonej lub nieskończonej liczbie, ale może być także przecięty krzywymi nieciągłości (…), nawet gdy całkowita długość krzywych nieciągłości jest nieskończona, [bez wypełnienia jakiejkolwiek części przedziału całkowania]”.

Wymiar fraktalny Hausdorffa zbioru Cantora jest równy \(\hbox{dim}_H(\mathcal{C})=\frac{\lg 2}{\lg 3}\approx 0{,}63<1,\) a \(\hbox{dim}_H([0,1])=1.\) Czym są więc zbiory o wymiarze dodatnim, ale mniejszym od jedności? Czy zbiór Cantora (Smitha) to jeszcze linia?

Możemy spekulować, że Smith, zanim wyraził tę myśl, wyobraził sobie dwuwymiarową wersję konstrukcji z przykładu 1 (dla \(m=3\)). Kwadrat jednostkowy \([0,1]^2\) dzielimy na 9 przystających kwadratów i usuwamy kwadrat (segment) w prawym dolnym rogu. Każdy z 8 pozostałych kwadratów dzielimy na 9 przystających kwadratów i w każdym z nich usuwamy kwadrat (segment) w prawym dolnym rogu. Dla pozostałych 64 kwadratów operację powtarzamy. Kontynuując tę operację w nieskończoność, otrzymamy zbiór, który „nie wypełnia jakiejkolwiek części kwadratu \([0,1]^2\)”. Pole pozostałe w \(k\)-tym kroku konstrukcji jest równe \(\big(\frac{8}{9}\big)^k\) i dąży do 0, gdy \(k\rightarrow\infty\) (rys. 4).

Rys. 4. Pierwsza, druga i czwarta iteracja konstrukcji płaskiego zbioru Smitha dla \((m=3)\)

Wymiar fraktalny Hausdorffa zbioru Smitha \(\mathcal{S}_3\) jest równy \(\hbox{dim}_H(\mathcal{S}_3)=\frac{\lg 8}{\lg 3}\approx 1{,}89<2,\) a \(\hbox{dim}_H([0,1]^2)=2.\) Czym są więc zbiory o wymiarze większym od jedności, ale mniejszym od dwóch? Czy to, co otrzymaliśmy, to jeszcze powierzchnia?

Dodatkowo prawa dolna granica powstałego zbioru jest wersją krzywej płatka śniegu (o nieskończonej długości) opublikowanej przez Helge von Kocha w 1904 roku.

Patrząc na opisane w artykule konstrukcje, nabieramy szacunku do pozornie prostych pytań: co to jest linia? co to jest powierzchnia? Odpowiedź na każde z nich… wcale nie jest łatwa!

I na koniec ciekawostka. Jeśli wyżej opisaną płaską konstrukcję Smitha wykonamy dla \(m=2,\) to otrzymamy\(\ldots\) wersję trójkąta Sierpińskiego (!), który został opublikowany w 1915 roku (rys. 5).

Rys. 5. Druga, czwarta i szósta iteracja konstrukcji płaskiego zbioru Smitha dla \((m=2)\)

Wymiar fraktalny Hausdorffa trójkąta Sierpińskiego \(\mathcal{T}\) jest równy \(\hbox{dim}_H(\mathcal{T})=\frac{\lg 3}{\lg 2}\approx 1{,}58<2.\)

Ale w 1875 roku Wacława Sierpińskiego nie było jeszcze na świecie! Ach, co by to było, gdyby Smith miał komputer\(\ldots\)

Literatura

1. H.J.S. Smith, „On the integration of discontinuous functions”, Proc. London Math. Soc. (1) 6 (1875), 140–153.

2. G. Cantor, „Uber unendliche lineare Punktmannichfaltigkeiten”, V, Math. Ann. 21 (1883), 545–591.