Na szachownicy o wymiarach \(8\times 8\) ustawiono osiem wież tak, aby żadne dwie wieże nie atakowały się wzajemnie. Pola szachownicy są rozdzielone pomiędzy wieże w następujący sposób: każde pole należy do najbliższej atakującej je wieży (przyjmujemy przy tym, że wieża atakuje też pole, na którym się znajduje). W przypadku gdy dwie atakujące dane pole wieże są w równej odległości od niego, każda z nich posiada połowę pola. Udowodnić, że dla każdej wieży całkowita powierzchnia posiadanych przez nią pól jest taka sama.
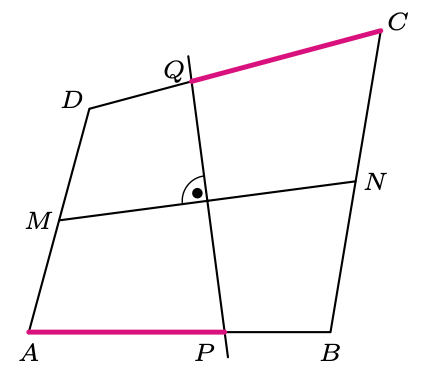
W czworokącie wypukłym \(ABCD\) boki \(AB\) i \(CD\) są równej długości, a punkty \(M\) i \(N\) są środkami \(AD\) i \(BC.\) Symetralna odcinka \(MN\) przecina boki \(AB\) i \(CD,\) odpowiednio, w punktach \(P\) i \(Q.\) Udowodnić, że \(AP = CQ.\)

Niech \(K\) i \(L\) będą środkami, odpowiednio, przekątnych \(AC\) i \(BD.\) Wtedy \(KN\) i \(LM\) są odpowiednio liniami środkowymi trójkątów \(ABC\) i \(ABD.\) Zatem czworokąt \(MKNL\) jest równoległobokiem.
Ponadto z równości \(AB = CD\) wynika, że \(NK = NL,\) czyli \(MKNL\) jest rombem. W szczególności punkty \(K\) i \(L\) leżą na symetralnej odcinka \(MN,\) czyli na prostej \(PQ.\) Dodatkowo \(\measuredangle APQ = \measuredangle NKL = \measuredangle NLK = \measuredangle DQP.\)
Poprowadźmy prostą równoległą do \(PQ\) przechodzącą przez punkt \(D.\) Niech \(T\) będzie punktem przecięcia tej prostej z prostą \(AB.\) Z twierdzenia Talesa łatwo dostajemy, że \(BP = PT.\) Ponadto \(TPQD\) jest trapezem o równych kątach przy wierzchołkach \(P\) i \(Q,\) czyli jest trapezem równoramiennym. W szczególności \(QD = PT = BP,\) skąd \(AP = CQ.\)
Wyznaczyć wszystkie funkcje \(f\colon \mathbb{R} \to \mathbb{R}\) takie, że dla dowolnych liczb rzeczywistych \(x,\) \(y\) spełniona jest równość \[(y+1)f\big(yf(x)\big)=yf\big(x(y+1)\big).\]
Kładąc \(y=0,\) dostajemy, że \(f(0)=0.\) Jeśli \(f(x_{0})=0\) dla pewnego \(x_{0}\neq 0,\) to kładąc \(x=x_{0},\) dostaniemy, że \(y f(x_0(y+1)) =0\) dla dowolnego \(x\in \mathbb{R},\) więc \(f\equiv 0\) – i jest to pierwsze rozwiązanie równania.
Załóżmy teraz, że \(f(x)=0\) wtedy i tylko wtedy, gdy \(x=0.\) Przypuśćmy, że dla pewnej liczby rzeczywistej \(a\neq 0\) mamy \(f(a)\neq a.\) Połóżmy \(x=a\) i \(y=\frac{a}{f(a)-a},\) wtedy \[\frac{f(a)}{f(a)-a} \cdot f\left(\frac{af(a)}{f(a)-a}\right) = \frac{a}{f(a)-a}\cdot f\left(\frac{af(a)}{f(a)-a}\right).\] Zauważmy jednak, że \(f\left(\frac{af(a)}{f(a)-a}\right )\neq 0,\) gdyż \(\frac{af(a)}{f(a)-a}\neq 0,\) zatem dzieląc obie strony powyższej równości przez \(f\left(\frac{af(a)}{f(a)-a}\right ),\) dostajemy równość \[\frac{f(a)}{f(a)-a}= \frac{a}{f(a)-a},\] z której oczywiście wynika, że \(f(a)=a\) – sprzeczność z założeniem. Wobec tego \(f\) jest identycznością.
Dwie jednakowe, wykonane z dielektryka kulki, o promieniu \(r\) każda, umieszczono w odległości \(R\) od siebie, przy czym \(R \gg r.\) Na jedną z nich wprowadzono ładunek \(q.\) Następnie odległość między kulkami zwiększono \(k\) razy. Jaki ładunek, \(Q,\) należy wprowadzić na jedną z nich po rozsunięciu, aby siła, z jaką na siebie oddziałują, była w obu przypadkach taka sama?
Poniżej jakiej długości fale dźwiękowe w gazie podlegają silnemu tłumieniu?