Afiliacja: Student, Uniwersytet Warszawski
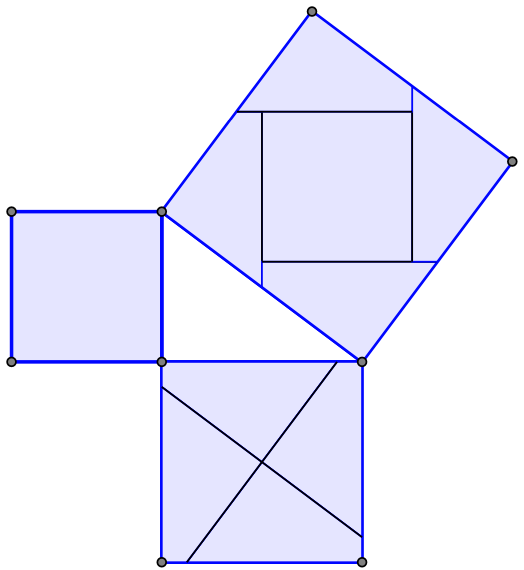
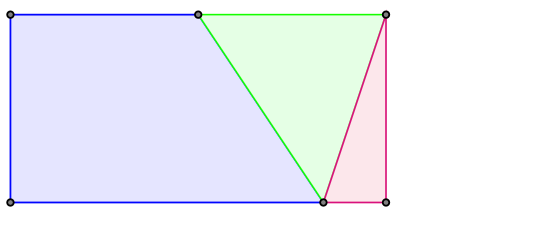
Myślę, że wszyscy dobrze znają jedno z najpopularniejszych twierdzeń na świecie – twierdzenie Pitagorasa. Jest wiele jego dowodów, a jeden z bardziej znanych polega na charakterystycznym pocięciu kwadratów zbudowanych na przyprostokątnych i złożeniu z tak otrzymanych kawałków kwadratu zbudowanego na przeciwprostokątnej.
Rys. 1
Można też spojrzeć na ten dowód z nieco innej perspektywy. Mając dwa kwadraty, umiemy je pociąć i złożyć z nich inny, którego pole jest sumą pól kwadratów początkowych. Narzucają się więc pytania: Czy inne figury mają tę samą cechę? Czy z dwóch trójkątów równobocznych można złożyć trójkąt równoboczny? A może da się kwadrat rozciąć i poskładać w trójkąt równoboczny? Jak się okazuje, odpowiedź na wszystkie te pytania jest twierdząca. Nie ma więc znaczenia kształt wielokąta, a jedynie jego pole. Okazuje się, że mamy następujące twierdzenie:
Twierdzenie Bolyaia–Gerwiena
Wielokąt \(A\) można pociąć prostymi i tak powstałe elementy złożyć w wielokąt \(B\) wtedy i tylko wtedy, gdy \(A\) i \(B\) mają równe pola.
Poruszony urokiem tego twierdzenia bezzwłocznie chwyciłem za długopis i kartkę w celu znalezienia dowodu. Ogólność tego zagadnienia nie pozwala na natychmiastowe rozpoczęcie rozwiązywania, więc zacząłem od opracowania planu działania.
Pomysł polega na znalezieniu pewnej recepty takiej, że postępując według niej, uda nam się wykonać taki ciąg cięć i sklejeń, aby z wielokąta \(A\) złożyć wielokąt \(B.\) Taka procedura może wyglądać następująco:
Redukujemy problem do trójkątów – poprzez rozcięcie wielokąta na trójkąty.
W następnym kroku rozcinamy trójkąt i składamy z jego kawałków kwadrat.
Ostatecznie kwadraty krok po kroku łączymy w jeden.
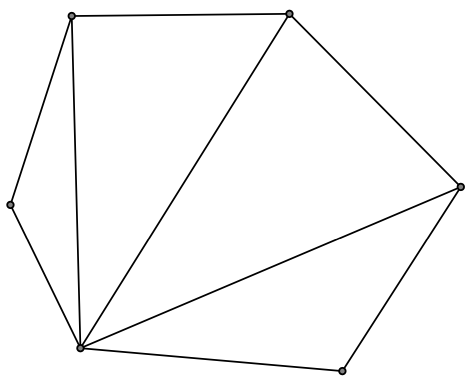
Rys. 2W przypadku wypukłym wystarczy rozciąć wzdłuż \(A_1A_3,\) \(A_1A_4,\) \(\ldots,\) \(A_1A_{n-1},\) gdzie \(A_1\ldots A_n\) jest rozpatrywanym wielokątem
Rys. 3
Rys. 4
Rys. 5
To będzie oznaczać koniec dowodu, bo \(B\) także będziemy umieli złożyć w kwadrat. Z założenia o równości pól kwadraty te muszą być przystające. Jeśli linie cięcia narysujemy na jednym kwadracie, dostaniemy podział, z którego można złożyć zarówno wielokąt \(A,\) jak i \(B\) – czyli \(A\) można pociąć na kawałki, z których złożymy \(B.\) Dowód w drugą stronę jest prosty, więc nie traćmy na niego czasu.
Dowód
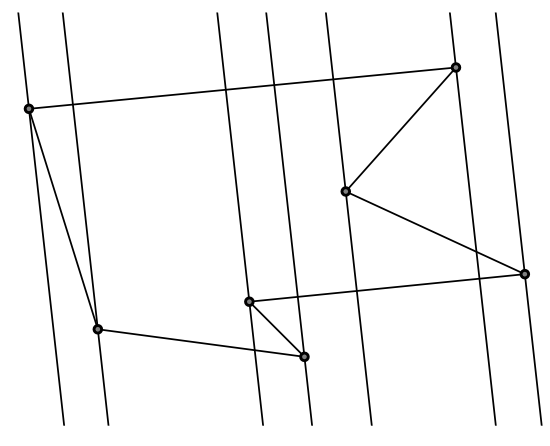
Dowolny wielokąt można pociąć na trójkąty. Jasne jest, że nie będzie problemu z pocięciem wielokąta wypukłego (rys. 2). Z wielokątem wklęsłym musimy być nieco ostrożniejsi. Pomysł jest taki: potnijmy go na plasterki. Wybierzmy taką prostą, żeby nie była równoległa do żadnego boku, a następnie przez każdy wierzchołek prowadźmy prostą równoległą do wybranej. Taka metoda podzieli nam wielokąt
na trójkąty i trapezy (dlaczego?), a trapez można rozciąć na dwa trójkąty po dowolnej z jego przekątnych.
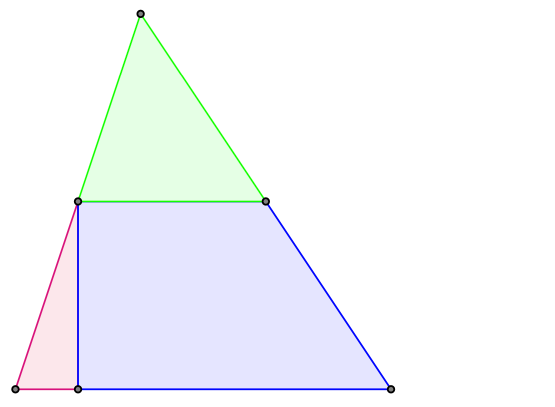
Wykażemy, że trójkąt można pociąć i z otrzymanych elementów złożyć kwadrat. Weźmy dowolny trójkąt i przetnijmy go wzdłuż prostej łączącej środki dwóch boków, między którymi jest największy kąt. Tak odcięty trójkąt obróćmy o \(180^{\circ}\) i przyłóżmy do drugiej części tak, aby powstał równoległobok. Następnie rozetnijmy tak powstały równoległobok wzdłuż krótszej z jego wysokości i przesuńmy odcięty trójkąt o wektor równy co do długości i równoległy do dłuższego boku równoległoboku (rys. 4 i 5). Tak powstanie prostokąt. (Pytanie do Czytelnika: Czemu na samym początku konstrukcji wybraliśmy największy kąt w trójkącie?).
Pozostaje pytanie, jak złożyć kwadrat z kawałków prostokąta.
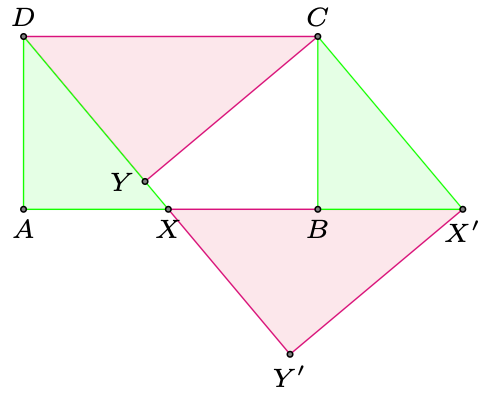
Weźmy prostokąt \(ABCD\) o bokach \(AD = a\) i \(AB = b\) i bez straty ogólności przyjmijmy \(a<b\) (rys. 6). Wybierzmy punkt \(X\) na boku \(AB\) oraz przez \(Y\) oznaczmy rzut punktu \(C\) na prostą \(DX.\) Przyjmijmy tymczasowo, że \(Y\) leży na odcinku \(DX.\) Dodatkowo oznaczmy przez \(x\) i \(y\) odpowiednio długości odcinków \(DX\) i \(CY.\) Jeśli teraz przesuniemy trójkąt \(AXD\) o wektor \(\overrightarrow{AB}\) i trójkąt \(CDY\) o wektor \(\overrightarrow{DX},\) otrzymamy prostokąt o bokach \(x\) i \(y,\) bo przesunięcia zachowują kąty między prostymi. Wystarczy tak dobrać \(x,\) żeby zachodziła równość \(x=y.\) Pole prostokąta przed i po tych przesunięciach jest takie samo, tj. \(ab=xy.\) Zatem potrzeba i wystarczy, aby \(x=\sqrt{ab}.\) Zastanówmy się teraz, kiedy opisana konstrukcja jest możliwa. Istnienie punktu \(X\) na odcinku \(AB\) spełniającego \({DX=\sqrt{ab}}\) jest równoważne nierówności \(DA\leq DX\leq DB,\) czyli \({a^2\leq ab\leq a^2+b^2},\) co jest zawsze prawdą dla \(a\leq b\) (patrz uzasadnienie na marginesie). Natomiast punkt \(Y\) leży na odcinku \(DX\) dokładnie wtedy, gdy \[DY \leq DX,\] czyli jeśli \[b^2 - y^2 \leq x^2,\] a to po wstawieniu \(x=y=\sqrt{ab}\) jest równoważne \[b \leq 2a.\] Tak więc prostokąt damy radę pociąć i złożyć w kwadrat, o ile zachodzi \({a\leq b \leq 2a}.\)
Rys. 6
Dla \(a,b\geq 0\) zachodzi \(ab\leq 2ab\leq a^2+b^2.\) Aby uzasadnić drugą nierówność, wystarczy zapisać ją w równoważnej postaci \((a-b)^2\geq 0.\)
Oczywiście byłoby dużo prościej, gdybyśmy mogli wycinać ujemne pole, ale to już byłoby inne twierdzenie.
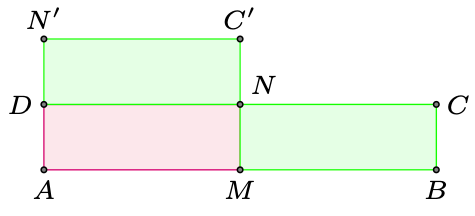
Oczywiście nie każdy prostokąt ma boki o długościach spełniających taką nierówność. Dla pozostałych prostokątów zastosujemy konstrukcję pomocniczą. Oznaczmy przez \(M\) i \(N\) środki boków \(AB\) i \(CD\) prostokąta \(ABCD.\) Wówczas, wykonując przesunięcie prostokąta \(MBCN\) o wektor \(\overrightarrow{MD},\) otrzymamy prostokąt o bokach długości \(2a\) i \(\frac{b}{2}.\) Zwróćmy uwagę na to, że takie cięcie możemy wykonywać dowolnie dużo razy.
Rys. 7
Z prostokąta o bokach \(a\) i \(b\) złożymy w ten sposób prostokąt o bokach \(a'\) i \(b'\) spełniających żądaną nierówność. Oznaczmy przez \(k\) największą liczbę całkowitą nieujemną, spełniającą nierówność \(2^{2k}a \leq b.\) Jeśli \(b\leq 2^{2k+1}a,\) to wykonując \(k\) cięć, otrzymamy prostokąt o bokach \(a' = 2^ka\) i \(b' = \frac{b}{2^k},\) którego boki spełniają pożądaną nierówność. Jeśli natomiast \(b \geq 2^{2k+1}a,\) to zauważmy, że z definicji \(k\) zachodzi także \(2^{2k+2}a\geq b.\) Tak więc możemy napisać: \[\frac{b}{2^{2k+1}} \geq a~\geq \frac{b}{2^{2k+2}} \iff 2\cdot\frac{b}{2^{k+1}}\geq 2^{k+1}a~\geq \frac{b}{2^{k+1}}.\] Oznacza to, że wykonując \(k+1\) cięć, otrzymamy prostokąt o bokach \(a' = 2^{k+1}a\) i \(b' = \frac{b}{2^{k+1}},\) tak że spełniona jest nierówność \(b' \leq a' \leq 2b'.\)
Polecamy również zapoznać się z artykułem Wiktora Bartola z \(\Delta^8_{08}\), w którym przedstawiony jest nieznacznie inny sposób cięcia.
Podsumujmy teraz dowód. Wykazaliśmy, że każdy trójkąt umiemy złożyć w prostokąt. Jeśli boki prostokąta spełniają odpowiednie warunki, to umiemy go złożyć w kwadrat. Natomiast jeśli tych warunków nie spełniają, to możemy wymusić je, przekształcając prostokąt w inny. Jako że umiemy złożyć dwa kwadraty w jeden, to indukcyjnie po pocięciu wielokąta na trójkąty, trójkątów w prostokąty, a prostokątów w kwadraty – damy radę połączyć te kwadraty w jeden. Złożyliśmy więc z dowolnego wielokąta kwadrat, tym samym z kwadratu każdy wielokąt. Oczywiście to spostrzeżenie kończy dowód. \(\Box\)
Jeśliby próbować uogólnić to twierdzenie do na przykład \(3\) wymiarów, to otrzymamy twierdzenie fałszywe. Okazuje się, że nie da się pociąć np. czworościanu foremnego płaszczyznami, a następnie złożyć sześcianu o tej samej objętości. Jeszcze w 1900 roku nie było to wiadome, a pytanie o to uogólnienie znalazło się na stworzonej przez Davida Hilberta liście 23 problemów istotnych dla rozwoju matematyki. Czytelnika zainteresowanego tym zagadnieniem odsyłam do artykułu Marka Kordosa z \(\Delta^{8}_{08}\).
Zwróćmy uwagę na to, że podczas dowodzenia nie szczędziliśmy nożyczek. Można na to zagadnienie spojrzeć właśnie przez pryzmat szukania minimalnej liczby cięć. Niemal 50 lat temu w Delcie \(\Delta^4_{75}\) pojawił się na ten temat artykuł autorstwa Alfreda Tarskiego. Jest to bardzo ciekawy tekst, który polecam wszystkim lubiącym wycinanki Czytelnikom.