* Wydział Matematyki, Informatyki
i Mechaniki, Uniwersytet Warszawski
** Uniwersytet Oksfordzki
W 2011 roku w czasopiśmie PLoS ONE ukazał się artykuł, w którego tytule autor zadał pytanie: Kto jest najlepszym tenisistą w historii? Aby na to pytanie odpowiedzieć, stworzył i przeanalizował sieć meczy tenisowych, w której wierzchołkami są tenisiści, a krawędzie reprezentują ich mecze. Następnie autor użył algorytmu PageRank (który za moment objaśnimy) do oceny ważności poszczególnych wierzchołków, i okazało się, że najlepszym tenisistą w historii jest… (werble) Jimmy Connors! Czy ten wynik jest dobry? To trudno powiedzieć. My zastanowimy się jednak nad innym pytaniem – dlaczego, do licha, użył PageRanka? Musimy się w tym celu cofnąć do lat dziewięćdziesiątych.
F. Radicchi. Who is the best player ever? A complex network analysis of the history of professional tennis. PLoS ONE (2011).
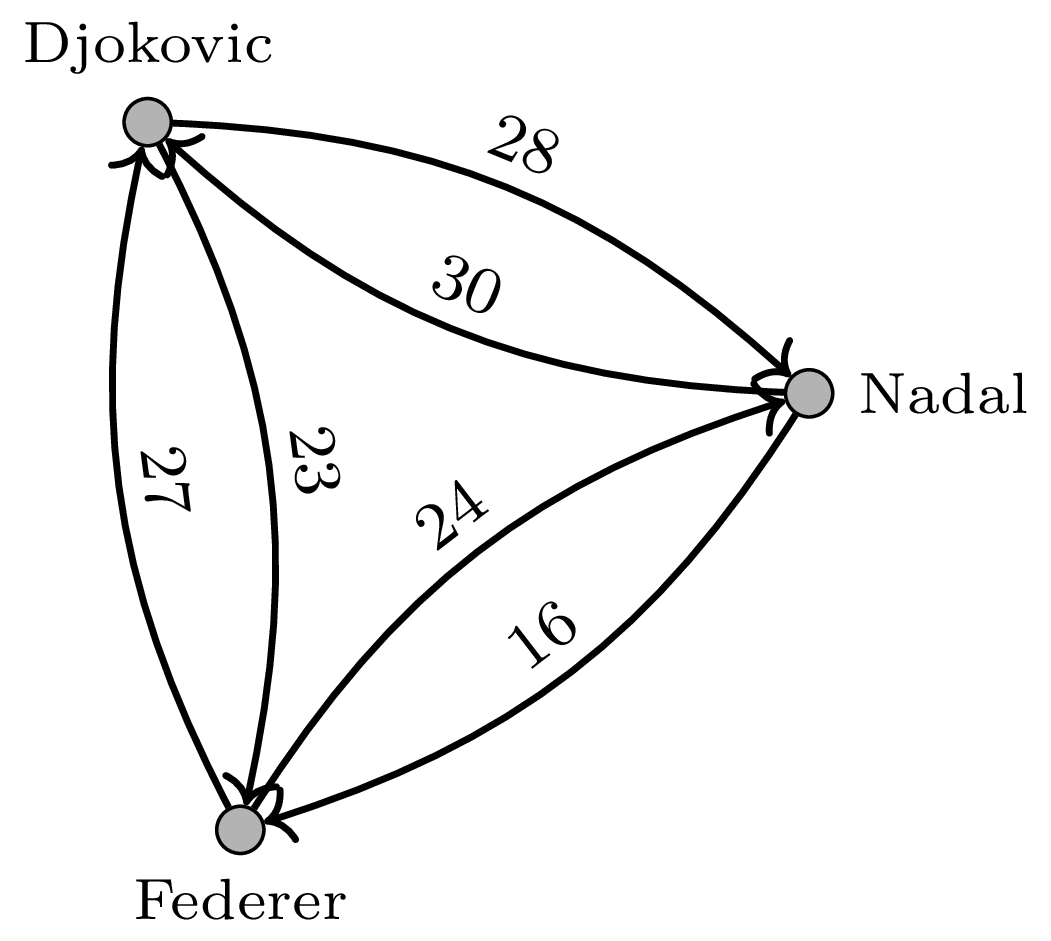
Sieć meczy tenisowych pomiędzy Wielką Trójką. Waga krawędzi oznacza jej krotność, czyli liczbę meczy wygranych przez gracza, do którego krawędź prowadzi
Jak PageRank działa?
Kiedyś Internet nie wyglądał tak jak teraz. Najpierw nie wyglądał w ogóle, bo go nie było, a nawet jak już był, to na początku był dość brzydki. Zanim powstała wyszukiwarka Google, ludzie wcale nie używali Binga i DuckDuckGo, bo ich też jeszcze nie było. Były duże katalogi stron, posegregowane na różne sposoby, a wyszukiwarki, które istniały, nie potrafiły znaleźć nic sensownego. Było naprawdę nieciekawie.
Na szczęście wszystko zmieniło się na przełomie XX i XXI wieku za sprawą dwóch pomysłowych i pracowitych doktorantów z Uniwersytetu Stanforda: Larry’ego Page’a i Sergeya Brina. W ramach projektu na studiach opracowali oni metodę oceny ważności stron w Internecie, nazwaną PageRankiem. Sama ocena nie była może tak istotna – wyszło im, że najważniejsza w Internecie jest strona ,,Download Netscape Software”. Przełomowy był jednak pomysł, aby zbudować wyszukiwarkę, która będzie brała te oceny pod uwagę przy wyświetlaniu wyników. Page i Brin szybko stali się niesamowicie bogaci i obecnie znajdują się w dziesiątce najbogatszych ludzi świata. Uniwersytet Stanforda – na pocieszenie, że nie ukończyli oni swoich doktoratów i nie pracują już w nauce – został natomiast właścicielem patentu, na którym zarobił 336 milionów dolarów.
Netscape był wówczas najpopularniejszą przeglądarką internetową.
Twórcy PageRanka w raporcie technicznym pod śmiałym tytułem The PageRank Citation Ranking: Bringing Order to the Web, w którym prezentują swoją metodę, z dumą piszą, że na wywołane hasło ,,university” na pierwszym miejscu pojawia się Uniwersytet Stanforda, a nie jakiegoś tam Oregonu.
Sama metoda działania PageRanka nie była żadną rewolucją. W literaturze naukowej tematem oceny elementów w sieci powiązań zajmowano się od lat. Już w roku 1949 uproszczoną wersję PageRanka zaproponował John R. Seeley w czasopiśmie zajmującym się eksperymentalną psychologią, starając się zmierzyć, kto jest najpopularniejszym dzieckiem w grupie. Autorzy nie znali jednak tej pracy (najwyraźniej nie znaleźli jej w Google Scholar), dlatego PageRanka wymyślili na nowo. Opierali się natomiast na coraz bardziej popularnym wówczas pomyśle, aby istotność strony powiązać z liczbą prowadzących do niej linków.
John R. Seeley. The net of reciprocal influence. A problem in treating sociometric data. Canadian Journal of Experimental Psychology (1949).
Idea ta dość dobrze działała przy ocenie prestiżu czasopism naukowych na podstawie liczby cytowań ich artykułów. Jednak w Internecie ocena strony poprzez samą liczbę prowadzących do niej linków nie jest dobrym pomysłem. Po pierwsze, w trywialny sposób możemy stworzyć milion stron, które będą do nas linkowały. Po drugie, link linkowi nierówny – jeżeli kieruje do nas bardzo popularna strona, to taki link jest dużo cenniejszy, niż gdy ktoś wspomni o nas na swoim blogu, który czyta tylko jego mama. Dlatego też w uproszczonej wersji PageRanka link ze strony \(A\) do strony \(B\) zwiększa ocenę \(B\) nie o \(1,\) ale o ocenę \(A\) podzieloną przez liczbę linków na stronie \(A.\) Oznacza to, że każda strona ,,rozdziela” swoją istotność po równo pomiędzy strony, do których prowadzi (a bardziej precyzyjnie, pomiędzy linki, które przekazują je stronom). W szczególności zwielokrotnienie linków na jednej stronie (zachowując proporcje między nimi) nie zmieni żadnej stronie oceny.
Impact Factor, stosowany do oceny czasopism, to właśnie średnia liczba cytowań wszystkich prac z danego roku.
Na Internet możemy patrzeć po prostu jak na graf skierowany, czyli pewien zbiór wierzchołków \(V\) reprezentujących strony internetowe i zbiór krawędzi \(E,\) czyli par wierzchołków reprezentujących linki. Wówczas uproszczony PageRank (oznaczany \({UPR}(v)\) dla \(v\)) jest rozwiązaniem następującego układu równań: \[{UPR}(v) = \sum_{(u,v) \in E}\frac{{UPR}(u)}{\deg^{+}(u)}\ \ \ \mbox{ dla każdego }v \in V,\] gdzie \(\deg^{+}(u)\) to liczba linków na stronie \(u,\) czyli inaczej krawędzi wychodzących z \(u.\) Jest to równanie rekurencyjne, więc nie jest oczywiste, ile ma rozwiązań. Jeżeli w grafie można dojść po krawędziach z każdego wierzchołka do każdego innego, czyli jest silnie spójny, to to równanie ma dokładnie jedno dodatnie rozwiązanie (z dokładnością do przemnożenia przez stałą). Jeżeli tak nie jest, sprawa się komplikuje. Dziwne wydaje się także to, że strony bez żadnych kierujących do nich linków mają zerową istotność, więc linki z nich również się nie liczą. Dlatego też właściwy PageRank wprowadza jedną drobną modyfikację – dodaje każdej stronie pewną małą bazową istotność \(b,\) ale w zamian lekko zmniejsza sumaryczny zysk z linków prowadzących do tej strony. Zysk mnożony jest przez współczynnik tłumienia \(\alpha \in (0,1),\) zwykle odrobinę mniejszy niż \(1\) (np. \(0{,}85\) lub \(0{,}9\)). Prowadzi to do następującego układu równań: \[{PR}(v) = \alpha \sum_{(u,v) \in E}\frac{{PR}(u)}{\deg^{+}(u)}+ b \ \ \ \mbox{ dla każdego }v \in V.\tag{$\star$}\] Tak uzyskany układ równań, dla ustalonego \(\alpha\) i \(b,\) ma już zawsze jedno unikalne rozwiązanie. Dowód tego faktu, dla trochę bardziej zaawansowanych Czytelników, znajduje się na marginesie.
Definicja dla grafów nieskierowanych jest taka, jakby każdą krawędź nieskierowaną zastąpić dwiema krawędziami skierowanymi w obie strony.
W oryginalnej pracy wartości bazowe \(b\) mogły być różne dla różnych wierzchołków i odpowiadały ,,źródłu istotności”. Autorzy rozważali na przykład ustawienie niezerowych wartości tylko niektórym stronom.
Dowód unikalności rozwiązania (\(\star\)): W postaci macierzowej układ równań zapisać możemy jako \(PR = \alpha \cdot \hat{A}^{T} \cdot PR + b \cdot \mathbb{1}^{T},\) gdzie \(\mathbb{1}\) jest wektorem jedynek, a \(\hat{A}\) jest znormalizowaną wierszowo macierzą sąsiedztwa, czyli \(\hat{A}[u,v]\) to liczba krawędzi z \(u\) do \(v\) podzielona przez \(\deg^{+}(u)\) lub \(0,\) jeżeli krawędzi z \(u\) do \(v\) nie ma. Dostajemy \((\mathbb{I}- \alpha \cdot \hat{A}^{T}) PR = b \cdot \mathbb{1}^{T},\) gdzie \(\mathbb{I}\) jest macierzą identycznościową. Macierz \((\mathbb{I}- \alpha \cdot \hat{A}^{T})\) jest odwracalna, bo jest przekątniowo dominująca, co daje nam: \(PR = b \cdot (\mathbb{I}- \alpha \cdot \hat{A}^{T})^{-1}\cdot \mathbb{1}^{T}.\)
W literaturze pojawiają się różne definicje PageRanka, ale właśnie powyższym równaniem jest on zdefiniowany w oryginalnej pracy. Jedyną małą różnicą jest to, że autorzy mnożyli także wartość bazową (\(b\)) przez \(\alpha.\) Łatwo zauważyć, że mnożenie przez \(\alpha,\) jak i w ogóle wartość \(b,\) nie ma zbytniego znaczenia, a tylko przeskalowuje wartości PageRanka: jeżeli przykładowo przemnożymy \(b\) przez \(2,\) to wartości PageRanka też się podwoją. Wynika to z tego, że takie wartości spełniają w sposób oczywisty równanie rekurencyjne \((*),\) a skoro rozwiązanie równania jest jedno, to musi być właśnie to. Będziemy więc zasadniczo przyjmowali \(b=1,\) ale inne wartości też nam się zaraz przydadzą.
Podstawowym sposobem definiowania PageRanka jest układ równań, jednak ma on też elegancką interpretację opartą na błądzeniu losowym. Więcej na ten temat można przeczytać w artykule Google w łańcuchach Łukasza Rajkowskiego, \(\Delta ^{11}_{19}\).
Przyjmijmy, że graf jest silnie spójny i niech \(b = (1-\alpha)/n,\) gdzie \(n\) jest liczbą wierzchołków. Możemy sobie teraz wyobrazić osobę, która ,,surfuje” po Internecie (tak się mówiło, kiedy powstawał PageRank…): zaczyna od losowej strony i potem klika losowe linki. Jednak na każdej stronie z małym prawdopodobieństwem, \(1-\alpha,\) zamiast klikać link, zaczyna surfować od początku. Wówczas wartość PageRanka danej strony jest równa prawdopodobieństwu, że znajdziemy na niej internautę w bardzo odległej przyszłości (prawdopodobieństwu granicznemu).
Częste losowe restarty w komputerze mocno utrudniają pracę, a w PageRanku analizę. Okazuje się, że możemy jednak tego łatwo uniknąć, wystarczy po prostu pozwolić internaucie pójść spać. Rozpatrzmy następującego zasypiającego surfera.
Zasypiający surfer:
Surfer losuje stronę startową, każdą z równym prawdopodobieństwem. Następnie z prawdopodobieństwem \(\alpha\) klika losowy link na stronie, na której jest, a z prawdopodobieństwem \({1-\alpha}\) zamyka komputer i idzie spać. PageRank dla \(b=1/n\) jest oczekiwaną liczbą wizyt na stronie w tym procesie.Dowód pozostawiamy Czytelnikowi jako nietrudne ćwiczenie. Ta obserwacja, jak i wiele innych w tym artykule, pochodzi z pracy:
T. Wąs, O. Skibski. Axiomatic characterization of PageRank. Artificial Intelligence (2023).
A co, jeśli graf nie jest silnie spójny i mamy strony, które nie mają żadnych linków? Tu jest pewien problem – gdzie ma wtedy pójść surfer? Są różne koncepcje. Czasem mówi się na przykład, że z automatu zaczyna surfowanie od początku, od losowej strony, ale musimy uważać – taka definicja nie da wcale naszego równania rekurencyjnego! Możemy natomiast powiedzieć, że z wierzchołków bez krawędzi surfer przechodzi do… swoistego ,,czyśćca”, czyli wierzchołka, który ma tylko pętlę do siebie. Surfer kręci się wówczas w nim, aż wylosuje rozpoczęcie od początku. PageRank będzie odpowiadał prawdopodobieństwom granicznym tego procesu, chociaż nie będzie sumował się do jedynki, bo dodatkowy wierzchołek trochę jej ,,zje”.
O ile dla osób znających PageRanka głównie z procesu losowego sumowanie do \(1\) może się wydawać ważne, o tyle przy analizie realnych sieci z milionami wierzchołków cecha ta jest nieistotna, a nawet niepożądana.
Jak PageRank nie działa
Za sprawą przeolbrzymiego sukcesu wyszukiwarki Google, PageRank stał się niezwykle popularny. Jest bardzo wiele powodów, dla których osoby, analizując skomplikowane sieci połączeń, spośród setek istniejących metod oceny sięgają po niego w pierwszej kolejności. Po pierwsze, można go szybko obliczyć. Po drugie, dobrze działa dla sieci WWW. Po trzecie, intuicyjnie ma sens. Po czwarte, jest popularny. Po piąte, jest dość skomplikowany, więc na pewno robi coś mądrego. Niestety, żaden z tych powodów nie świadczy o tym, że PageRank jest odpowiednim wyborem dla konkretnej sieci, nieraz kompletnie innej niż Internet.
Skupimy się na (nieuproszczonym) PageRanku, a dla uproszczonego radzimy sprawdzić, jak działa dla grafów nieskierowanych… Czy przypadkiem nie przypomina trochę stopnia wierzchołka?
Popatrzmy na parę przykładów. Zacznijmy od czegoś prostego – jak myślisz, Czytelniku, który wierzchołek jest najważniejszy w poniższym grafie?

Według PageRanka wierzchołki 2 i 6! Raczej przeczy to intuicji… To dlaczego PageRank tak zadziałał? Widać to z interpretacji z błądzeniem losowym – wierzchołki te mają sąsiada, który zawsze odeśle surfera z powrotem do nich.
\(v\) 1, 7 2, 6 3, 5 4 \({PR}(v)\) 3,36 5,90 5,53 5,42 PageRank dla linii 7 wierzchołków (rysunek obok), przyjmując \(\alpha=0{,}8\) i \({b = 1}.\) W liczenie PageRanka można się pobawić na stronie: https://centrality.mimuw.edu.pl/editor/.
A w poniższych grafach ważniejszy jest wierzchołek \(u\) czy \(v\)?
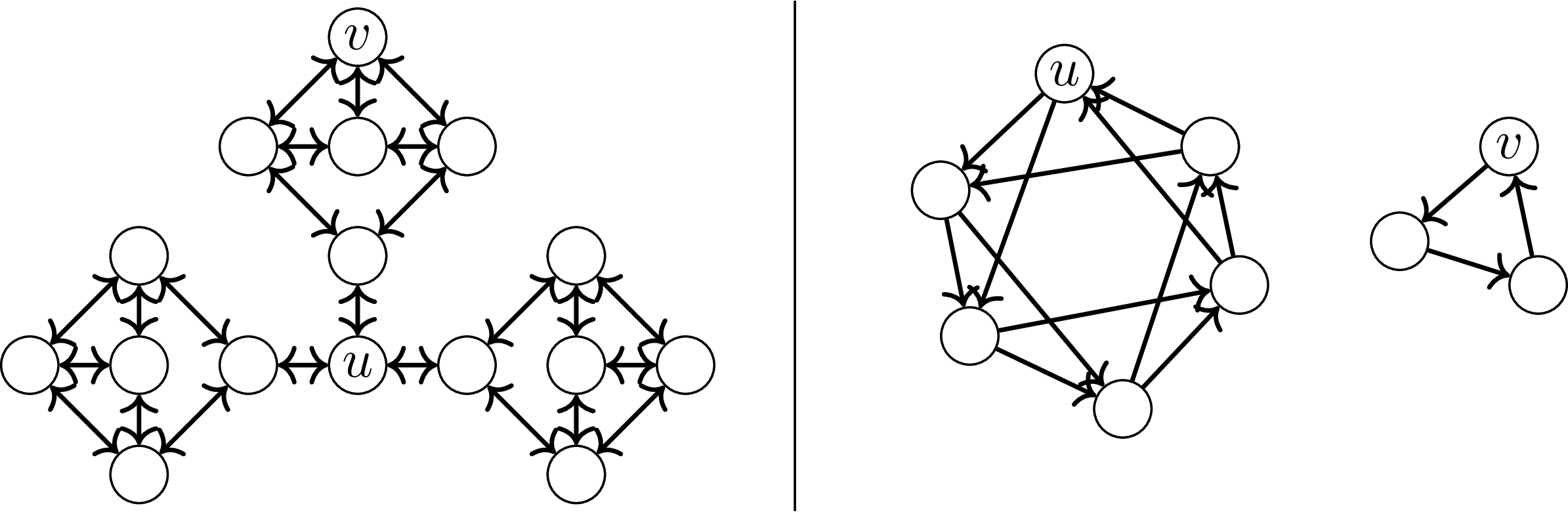
Wydaje się, że to wierzchołek \(u\) jest ważniejszy zarówno po lewej, jak i po prawej stronie. Po lewej stronie jest w ,,centrum” grafu, rozdziela graf na trzy części. Tak mówią też inne miary centralności: ma najmniejszą średnią odległość do innych wierzchołków, przechodzi przez niego dużo najkrótszych ścieżek. Po prawej stronie wierzchołek \(u\) jest w większym komponencie, ma krawędzie i ścieżki od większej liczby wierzchołków. Wbrew intuicji PageRank w obu przypadkach ocenia je jednak tak samo – w każdej \(n\)-wierzchołkowej silnie spójnej składowej suma PageRanków jest równa \(b \cdot n/(1-\alpha),\) a jeżeli wierzchołki są w niej symetryczne lub choćby mają takie same stopnie (wchodzący i wychodzące), to PageRank każdy ocenia na \(b/(1-\alpha).\)
Powyższe przykłady mogły się wydawać nieco sztuczne, wróćmy zatem do prawdziwej pracy naukowej i prawdziwej sieci meczy tenisowych. Wierzchołkami w tej sieci są tenisiści, a skierowanymi krawędziami – ich mecze: krawędź z A do B oznacza jeden mecz rozegrany pomiędzy A i B, wygrany przez B. Czy PageRank dla tej sieci daje sensowne wyniki? Wydaje się, że niestety nie.
Aby to zobaczyć, ograniczmy się na chwilę do meczy rozgrywanych przez Wielką Trójkę: Federera, Nadala i Djokovica (patrz margines na pierwszej stronie artykułu). Nie ulega wątpliwości, że Djokovic wypada tu najlepiej – ma dodatni bilans meczy zarówno z Federerem (30:28), jak i Nadalem (27:23). PageRank też wskazuje Djokovica jako najlepszego tenisistę – zgadza się! Zmodyfikujmy teraz trochę sztucznie graf, zastępując każdy przegrany mecz Djokovica dwoma meczami. Teraz ma już gorszy bilans od Federera i Nadala. A co na to PageRank? Nic! Jak już powiedzieliśmy wcześniej, powielenie każdego z wychodzących linków tę samą liczbę razy nie zmieni PageRanka żadnego wierzchołka. Nie tego jednak byśmy się spodziewali od sensownej miary.
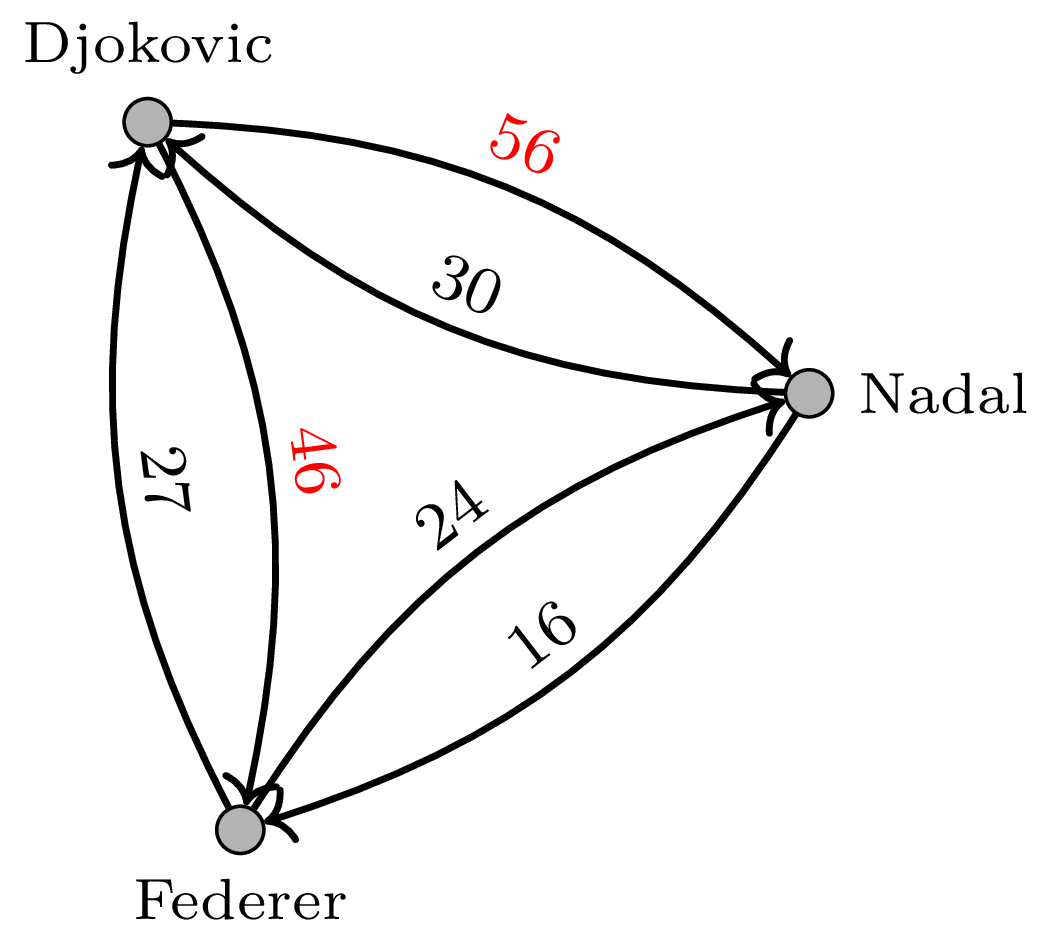
Powyższy graf powstał z podwojenia meczy przegranych przez Djokovica. PageRank jednak nadal daje największą wartość Djokovicowi, gdyż zarówno Nadal, jak i Federer przegrali z nim więcej razy niż ze sobą nawzajem. Czy jednak takiego wyniku byśmy oczekiwali w tej sytuacji?
A jakiej miary powinniśmy użyć? Wydaje się jednak bardziej właściwe, aby – jak w sieci cytowań – brać pod uwagę liczbę, a nie samą proporcję wychodzących krawędzi. Taką miarą jest na przykład centralność Katza, która zdefiniowana jest zasadniczo takim samym równaniem rekurencyjnym jak PageRank, ale bez dzielenia przez \(\deg^{+}(v).\) Więcej o tej, jak i o innych podobnych miarach, można przeczytać w artykule Jak Leo uratował klasowe wybory, \(\Delta ^{9}_{21}\).
Wracając zatem do początkowego pytania: czy powinniśmy stosować PageRanka w sieci meczów tenisowych? W sieci WWW działa on dobrze i stosowany był w przeróżnych sieciach. Lecz jak nauczyła nas formuła PageRanka, sama liczba poleceń to nie wszystko, ważne jest, skąd te polecenia pochodzą… My do tenisa go nie polecamy.