Afiliacja: [RW] Klub Naukowy Fenix, Instytut Fizyki PAN,
[HB] Wydział Nauk Ekonomicznych, Uniwersytet Warszawski
Zdobycze technologiczne
W 2018 roku Google dodał do systemu Android funkcję Digital Wellbeing (cyfrowy dobrostan), która pozwala ustawiać limity czasu korzystania z danej aplikacji na dany dzień. Możemy na przykład ustawić 15-minutowy limit na korzystanie z Instagrama; po upływie tego czasu ikona aplikacji zmienia kolor na szary, a sama aplikacja przestaje się uruchamiać. Podobne rozwiązanie wprowadziła również firma Apple w systemie iOS. Dlaczego ktoś miałby skorzystać z takiej funkcjonalności? Czym aktywowanie tego trybu różni się od po prostu wyłączenia aplikacji po upływie wyznaczonego czasu? Cynik mógłby powiedzieć, że nie ma w tym nic racjonalnego, a odpowiedzi na to pytanie powinien szukać psycholog, a nie ekonomista czy matematyk. Jednak przy pewnych założeniach takie zachowanie może być całkowicie racjonalne…
Mierzenie cierpliwości
1Zacznijmy od pytania, dlaczego w neoklasycznej ekonomii nie ma powodu, aby utrudniać sobie życie w przyszłości. Rozważmy hipotetyczną sytuację, w której mamy do wyboru dwie, ogólnie rzecz biorąc, satysfakcjonujące możliwości. Pierwsza z nich daje szybki rezultat, na przykład rozwiązanie jednego zadania z naszego ulubionego zbioru zadań. (Żeby nie komplikować zbytnio rachunków, założymy, że danego dnia możemy rozwiązać tylko jedno zadanie). Druga z nich wymaga pracy przez dłuższy czas, powiedzmy \(n\) dni, ale daje nam dużą satysfakcję z ukończenia, \(b\) razy większą niż rozwiązanie jednego zadania. Dla przykładu niech będzie to spisanie na czysto pracy na Konkurs Uczniowskich Prac z Matematyki (zgłoszenia do 30 kwietnia 2025!). Załóżmy, że sam proces spisywania pracy nie daje nam żadnej satysfakcji i że spisywanie pracy i rozwiązywanie zadania to alternatywa wykluczająca. Najbardziej naiwny model opisujący decyzję, czy spisywać, czy nie, porównuje naszą satysfakcję \(U\) z rozwiązania \(n\) zadań, \(U = n,\) z satysfakcją z wysłania pracy na konkurs, \(U = b,\) czyli usiądziemy do spisywania pracy, jeśli \(b > n.\) Problem polega na tym, że lepszy wróbel w garści niż gołąb na dachu, czyli, innymi słowy, zadanie dzisiaj jest warte więcej niż zadanie jutro. Klasyczny model ekonomiczny proponuje wprowadzenie stałej \(0 < q < 1,\) która mierzy naszą niecierpliwość (3). W tym modelu satysfakcję z przyszłych osiągnięć należy przemnożyć przez \(q\) podniesione do potęgi liczby dni oczekiwania. W takim razie satysfakcja z rozwiązania po jednym zadaniu przez \(n\) dni wynosi \(U = \sum_{i=0}^{n-1} q^i,\) a satysfakcja z wysłania pracy na konkurs wynosi \(U = q^{n-1} b.\) Zatem zabierzemy się do spisywania, jeśli \(q^{n-1} b > \sum_{i=0}^{n-1} q^i.\) Sumując szereg geometryczny i upraszczając, otrzymujemy warunek: \[(1-q) b + q > \frac{1}{q^{n-1}}.\] Prawa strona nierówności jest rosnącą funkcją \(n,\) więc jeśli kiedykolwiek podejmiemy decyzję, aby zacząć spisywać, to każdego kolejnego dnia będziemy coraz bardziej zmotywowani (będziemy potrzebowali mniej czasu na dokończenie spisywania pracy, co odpowiada zmniejszaniu \(n\)) i bez trudu zrealizujemy nasz plan.
Dyskontowanie niespójne czasowo
Co by się stało, gdyby nasza funkcja użyteczności wyglądała inaczej? Do przysłowia o wróblu pasują przecież wszystkie malejące funkcje, nie tylko funkcja wykładnicza. Dodajmy kolejny parametr, nazwijmy go \(a,\) który dodatkowo przeskalowuje, jak bardzo zależy nam na „dzisiaj” w porównaniu do ,,jutra”, a resztę pozostawmy bez zmian. W takiej sytuacji satysfakcja \(U\) z rozwiązywania zadań przez \(n\) dni z rzędu wyniesie \(U = a + \sum_{i=1}^{n-1} q^i,\) a satysfakcja z wysłania pracy na konkurs wciąż wynosi \(U = q^{n-1} b.\) Równie łatwo możemy obliczyć satysfakcję, którą osiągniemy w ciągu kolejnych \(n+1\) dni zamiast \(n\) dni. Będzie to odpowiednio \(U = a + \sum_{i=1}^n q^i\) oraz \(U = q^{n-1} b + q^n,\) gdzie człon \(q^n\) odpowiada jednemu dniu rozwiązywania zadań po wysłaniu pracy na konkurs. Jeśli \(a > 1,\) to okazuje się, że należy rozważyć jeszcze trzecią opcję, która może maksymalizować \(U\): zacząć spisywać dopiero od jutra, co daje wynik \(U = a + q^{n} b.\)
Gdy \(b q^{n-1} (1-q) > a - q^n,\) strategią maksymalizującą satysfakcję będzie zabranie się do pracy dzisiaj. Natomiast gdy \(b q^{n-1}(1-q) < 1 - q^{n},\) optymalną strategią będzie rozwiązywanie zadań i porzucenie konkursu. Jednak jeśli wartość \(b\) znajdzie się pomiędzy tymi dwiema granicami, pojawia się nowe optimum – zajmijmy się konkursem, ale dopiero od jutra. Istnieje jednak pewna pułapka. Świadomi naszej funkcji użyteczności zaczynamy się zastanawiać, jaką decyzję podejmiemy jutro – czy rzeczywiście będziemy trzymać się planu, czy ulegniemy pokusie szybkiej satysfakcji z rozwiązania pojedynczego zadania? Niestety możemy dojść do smutnej konkluzji: przy odpowiednio dużym \(n\) odroczymy przygotowanie pracy na konkurs o kolejny dzień (a potem znowu o kolejny i kolejny, aż \(n\) stanie się odpowiednio małe).
Znaleźliśmy się we frustrującej sytuacji, w której „ja dzisiaj” nie mogę dojść do porozumienia z „ja jutro”. Różne scenariusze dla przykładowych wartości \(n\) i \(q\) można porównać na rysunku (1). Z tego potrzasku może nas uratować zewnętrzny deadline – będziemy odkładać pracę na kolejny dzień aż do ostatniej chwili, gdy utrata szansy na dużą nagrodę stanie się zbyt kosztowna (obszar oznaczony jako prokrastynacja). Niestety czasami nawet to nie wystarczy (obszar oznaczony jako porażka). Zapału może zabraknąć nawet w ostatnim dniu, gdy \[b q^{n-1} (1-q) < q - a q + a - q^{n}.\]
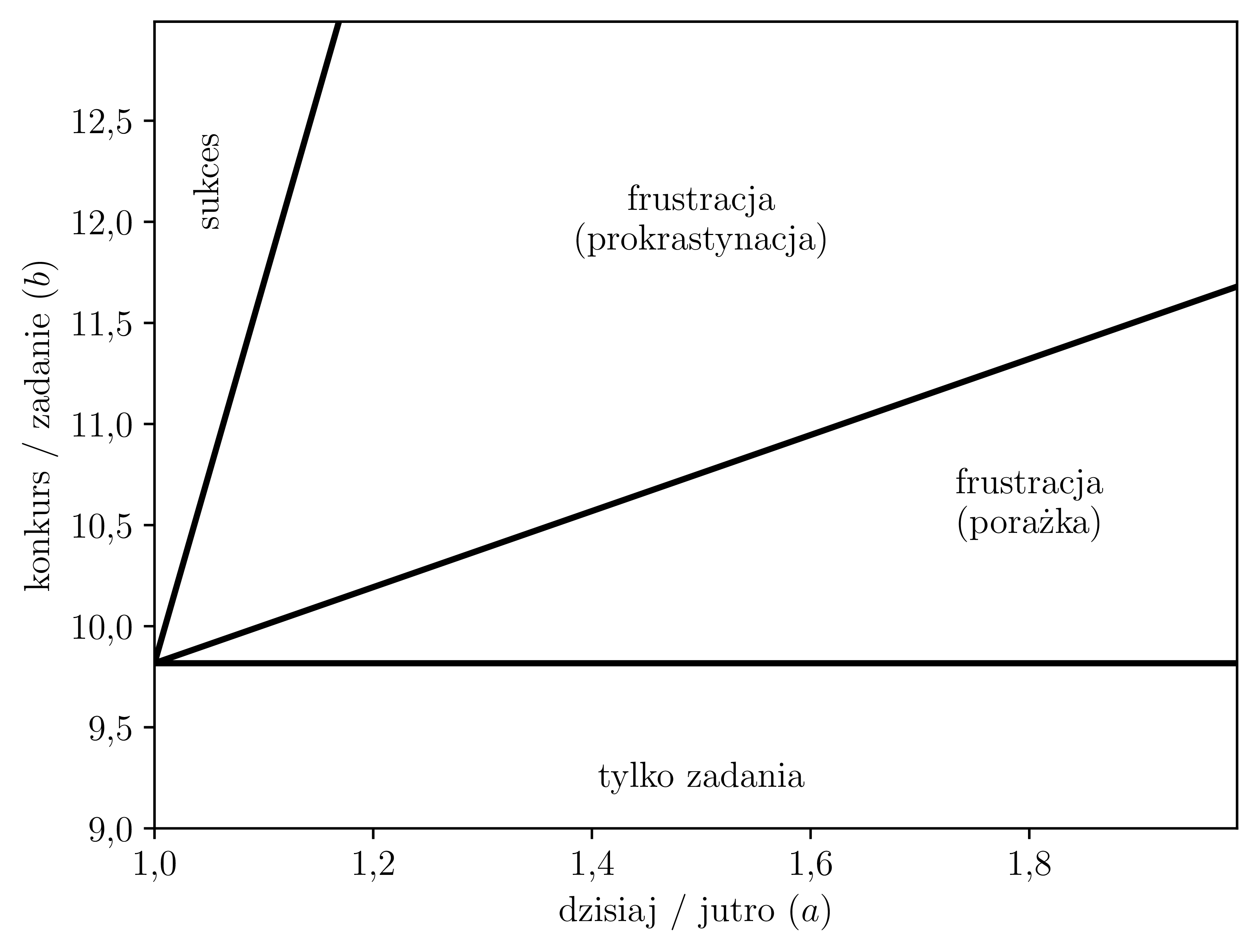 Rys. 1. Mapa optymalnych strategii dla \(n = 7\) i \(q = 0{,}9\)
Rys. 1. Mapa optymalnych strategii dla \(n = 7\) i \(q = 0{,}9\)
Na pomoc z szuflą
Zawiedzeni swoim słomianym zapałem idziemy po radę do starszego brata. Ten mówi, że może porozmawiać później, bo najpierw musi odśnieżyć przed domem. Wtedy doznajemy olśnienia – aby rozwiązać nasz problem, wystarczy wyręczyć brata dzisiaj.
Proponujemy mu następujący układ: my dzisiaj odśnieżymy, a ta niespecjalnie satysfakcjonująca czynność jest dla nas warta \(-c.\) W zamian brat odśnieży za nas za \(n\) dni, ale tylko jeśli złożymy pracę na konkurs. Brat oczywiście się zgadza, ponieważ nawet jeśli wierzy, że pracę złożymy, to jednak niepracowanie dzisiaj jest warte więcej niż niepracowanie za \(n\) dni.
Tym samym znaleźliśmy się w sytuacji, w której nasza satysfakcja wyniesie \(U = a(1-c) + q^n (b+c),\) jeśli od jutra zaczniemy pracować nad spisaniem pracy na konkurs. Z punktu widzenia ,,ja jutro” jedyną zmianą jest to, że wielkość nagrody wzrosła o \(c,\) co zwiększa nasze szanse na podjęcie się pracy jutro. Ta zmiana o \(c\) pozwala nam uniknąć porażki, jeśli jesteśmy odpowiednio blisko granicy porażka/prokrastynacja. Mały kolorowy czworobok na rysunku (2), odpowiadający tej sytuacji, nie sięga do granicy porażka/tylko zadania, ponieważ tam zysk z wejścia w kontrakt jest zbyt mały w porównaniu do straty satysfakcji dzisiaj. Innymi słowy, \(c\) jest za duże (mimo że już zawiązany kontrakt byłby skuteczny).
Jeszcze ciekawszy jest obszar nad granicą porażka/prokrastynacja – w przypadku celów, które nie mają zewnętrznie określonego terminu, możemy taki termin sami wyznaczyć i ,,kupić” go u brata za \(c(a - q^n)\) satysfakcji, wciąż dobrze wychodząc na takiej transakcji. Zwyczajnie, \(c(a - q^n)\) może być małe w porównaniu do straconej satysfakcji wynikającej ze słomianego zapału.
Podsumowując, w pewnym zakresie parametrów możemy zmusić ,,ja jutro” do współpracy, o ile mamy dostęp do drugiej osoby, na której możemy polegać (nawet jeśli ta osoba nie zachowuje się altruistycznie).
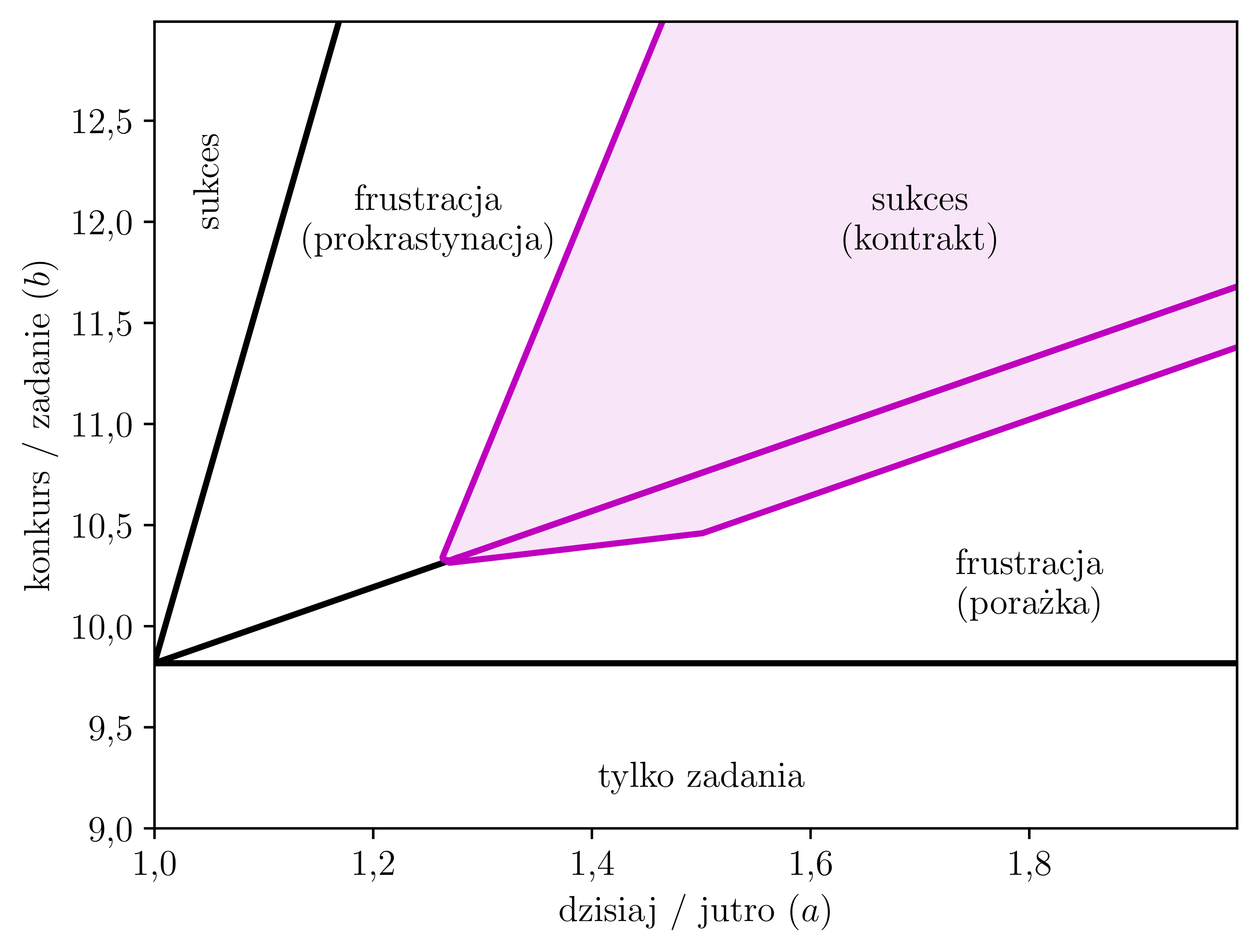 Rys. 2. Mapa optymalnych strategii dla \(n = 7,\) \(c = 0{,}3\) i \(q = 0{,}9\)
Rys. 2. Mapa optymalnych strategii dla \(n = 7,\) \(c = 0{,}3\) i \(q = 0{,}9\)
Zapotrzebowanie na zobowiązania
Świadomość możliwego konfliktu ze sobą z przyszłości pozwala wyjaśnić (albo przynajmniej opowiedzieć w ramach racjonalistycznej historii) wiele pozornie nieracjonalnych sytuacji. Dlaczego pracę dyplomową lepiej pisze się w kawiarni odległej od domu? Dlaczego zostawienie laptopa w pracy pomaga w odpoczynku? (1)
Zapotrzebowanie na zobowiązania, lub raczej brak dostępu do narzędzi do jego zrealizowania, jest jednym z wyjaśnień pozornie nieracjonalnych zachowań o bardziej ważkich konsekwencjach niż kolejna godzina spędzona na scrollowaniu. Właśnie za pomocą dyskontowania niespójnego czasowo Esther Duflo (Nagroda Nobla w 2019 r.) wyjaśnia zaskakująco niskie inwestycje w nawozy w Kenii (które mają oszołamiające stopy zwrotu, rzędu 50% rocznie). Tę publikację (z niezwykle ciekawą strategią badawczą) bardzo polecamy (2), nie tylko jako alternatywę dla spędzania czasu z telefonem.
1. G. Bryan, D. Karlan i S. Nelson. ,,Commitment devices”. W: Annual Review of Economics 2.1 (2010), s. 671–698.
2. E. Duflo, M. Kremer i J. Robinson. ,,Nudging farmers to use fertilizer: Theory and experimental evidence from Kenya”. W: American Economic Review 101.6 (2011), s. 2350–2390.
3. P. Wołowik. ,,Maksymalizacja zysków zarządzanego kapitału w różnych typach gier ekonomiczno-hazardowych”. W: Delta 10 (2005).