Zadania z matematyki nr 897, 898
Termin nadsyłania rozwiązań: 31 V 2025
Redaguje Marcin E. KUCZMA
897. Czworokąt wypukły \(ABCD\) ma obwód długości \(p\) oraz przekątne długości \(m\) i \(n.\) Punkt \(E\) jest czwartym wierzchołkiem równoległoboku \(ABCE.\) Udowodnić, że \({DE\le{p-m-n}}.\)
898. Wyznaczyć wszystkie pary liczb naturalnych \({m,n\ge1},\) dla których wielomian \({W(x)=x^m+x^n+1}\) jest podzielny przez trójmian \({T(x)=x^2+x+1}.\)
Zadanie 898 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązania zadań z numeru 11/2024
Przypominamy treść zadań:
889. Ciąg \((a_1,\ldots,a_N),\) długości \(N,\) ma wyrazy \({a_k\in\{2,3,5\}},\) z sumą \({a_1+\ldots+a_N=A}.\) Niech \({b_k=a_ka_{k+1}a_{k+2}a_{k+3}}\) (gdzie, cyklicznie, \({a_{N+i}=a_i}\)). Zakładamy, że każda z liczb \({b_1,\ldots,b_N}\) dzieli się przez \(30.\) Przyjmując jako znane wartości \(N,\) \(A\) (dla których istnieje co najmniej jeden ciąg \((a_k)\) o podanych własnościach) wyznaczyć wszystkie możliwe wartości sumy \({B=b_1+\ldots+b_N}.\)
890. W czworokącie wypukłym \(ABCD\) przekątne przecinają się w punkcie \(P\); boki \(BC\) i \(DA\) nie są równoległe, a ich symetralne przecinają się w punkcie \(Q\) (różnym od \(P\)), leżącym wewnątrz czworokąta. Trójkąty \(BQC\) i \(DQA\) są podobne. Udowodnić, że prosta \(PQ\) zawiera dwusieczne kątów \(APB\) i \(CPD.\)
889. Podzielność \({30{\mid}b_k}\) oznacza, że w każdej czwórce kolejnych wyrazów \(a_k,a_{k+1},a_{k+2},a_{k+3}\) są obecne liczby \(2,3,5\) oraz – powtórnie – jeszcze jedna z nich; nazwijmy ją \(c_k.\) Wówczas \({b_k=30c_k},\) zaś \({a_k+a_{k+1}+a_{k+2}+a_{k+3}=10+c_k}.\) Stąd \[\begin{aligned} B&=\sum_{k=1}^N b_k=30\sum_{k=1}^N c_k =30\sum_{k=1}^N(a_k+a_{k+1}+a_{k+2}+a_{k+3}-10)=30(4A-10N). \end{aligned}\] Jest to jedyna możliwa wartość sumy \(B.\)
890. Z określenia \(Q\) wynika, że trójkąty podobne \(BQC\) i \(DQA\) są równoramienne: \({QB=QC},\) \({QD=QA}.\) Oznaczmy \(\measuredangle{QBC}=\measuredangle{QCB}=\measuredangle{QAD}=\measuredangle{QDA}=\alpha.\) Niech \(R\) będzie drugim (poza \(Q\)) punktem przecięcia okręgów opisanych na tych trójkątach. Przyjmijmy (b.s.o.), że proste \(BC\) i \(DA\) przecinają się w punkcie leżącym na półprostych \(BC^\to\) i \(AD^\to\); wówczas punkt \(R\) leży w obszarze kąta wypukłego \(CQD\) (nie jest możliwe, by punkt \(C\) lub \(D\) leżał na ,,krótkim” łuku \(QR\) jednego z rozważanych okręgów, bo to by się kłóciło z wypukłością czworokąta \(ABCD\)). Mamy więc konfigurację, jak na rysunku.
W okręgach \(BQC\) i \(DQA\) widzimy kąty wpisane: \[\displaylines{ \measuredangle{BRQ}=\measuredangle{BCQ}=\alpha,\ \ \ \measuredangle{CRQ}=\pi-\measuredangle{CBQ}=\pi-\alpha,\cr \measuredangle{ARQ}=\measuredangle{ADQ}=\alpha,\ \ \ \measuredangle{DRQ}=\pi-\measuredangle{DAQ}=\pi-\alpha. }\] Z pierwszej i czwartej równości wynika, że punkt \(R\) leży na odcinku \(BD\); zaś z drugiej i trzeciej – że \(R\) leży na odcinku \(AC.\) To znaczy, że \(R\) jest punktem \(P\) z treści zadania. Równości pierwsza z trzecią pokazują, że prosta \(QR\) połowi kąt \(ARB\); zaś druga z czwartą – że ta prosta połowi kąt \(CRD.\) Zważywszy, że \({R=P},\) mamy to, co należało udowodnić.
Inna metoda (szkic): stosujemy inwersję o środku \(Q\) (i dowolnie ustalonym promieniu dodatnim). Półproste \(QA^\to,\) \(QB^\to,\) \(QC^\to,\) \(QD^\to,\) \(QP^\to\) przechodzą każda na siebie. Obrazami punktów \(A,B,C,D,P\) są punkty, które oznaczymy \(A^*,B^*,C^*,D^*,P^*,\) leżące odpowiednio na tych półprostych. W mocy pozostają równości \({QB^*=QC^*},\) \({QD^*=QA^*}.\) Obrazem prostej \(AC\) jest okrąg \(QA^*C^*,\) zaś prostej \(BD\) – okrąg \(QB^*D^*\) (każdy z nich z usuniętym punktem \(Q\)). Punkt \(P^*\) leży na obu okręgach.
Mamy udowodnić, że prosta \(QP\) tworzy równe kąty z prostymi \(AC\) i \(BD.\) Inwersja zachowuje równość kątów, więc wystarczy wykazać, że prosta \(QP^*\) tworzy równe kąty z okręgami \(QA^*C^*\) i \(QD^*B^*.\) Ponieważ \({\measuredangle{B^*QC^*}=\measuredangle{D^*QA^*}=\colon\,\varphi},\) obrót o kąt \(\varphi\) wokół \(Q\) przenosi trójkąt \(QA^*C^*\) na trójkąt \(QD^*B^*.\) Zatem te trójkąty są przystające – okręgi na nich opisane też są przystające – są więc symetryczne względem wspólnej cięciwy \(QP^*.\) Stąd wymagana równość kątów i teza zadania.
Zadania z fizyki nr 794, 795
Termin nadsyłania rozwiązań: 31 V 2025
Redaguje Elżbieta ZAWISTOWSKA
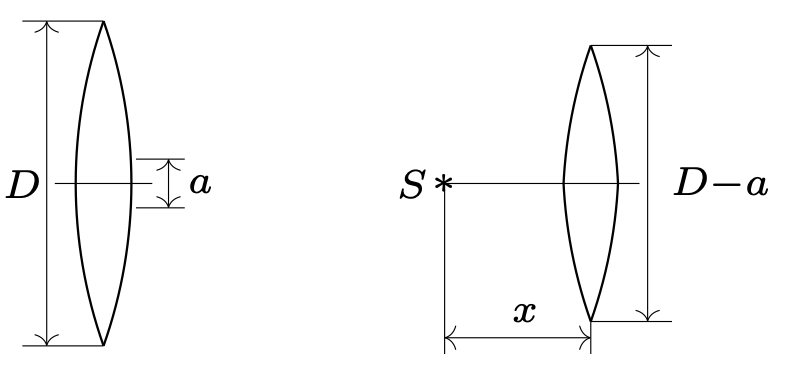
794. Z soczewki skupiającej o ogniskowej \(f=50\) cm i średnicy \(D=5\) cm wycięto środkowy pasek o szerokości 5 mm, a pozostałe części złożono ze sobą (rys. 1). W odległości \(x=75\) cm od soczewki umieszczono punktowe źródło światła monochromatycznego \(S.\) Korzystając z przybliżenia małych kątów, znaleźć maksymalną liczbę prążków obrazu interferencyjnego, jaka może powstać na ekranie za soczewką. Długość fali świetlnej \(\lambda =5\cdot 10^{-7}\,\)m.
795. Izolowaną metalową początkowo nienaładowaną płytkę oświetlano w czasie \(\tau\) światłem nadfioletowym. W wyniku tego z płytki wyleciała chmura elektronów, których prędkość początkowa była prostopadła do płytki i miała wartość \(v_0.\) Całkowita liczba elektronów, które wyleciały z jednostki powierzchni, wynosi \(n,\) elektron ma ładunek \(e\) i masę \(m.\) Znaleźć grubość chmury \(h\) po czasie \(t\) od zakończenia naświetlania (rys. 2).
Rozwiązania zadań z numeru 11/2024
Przypominamy treść zadań:
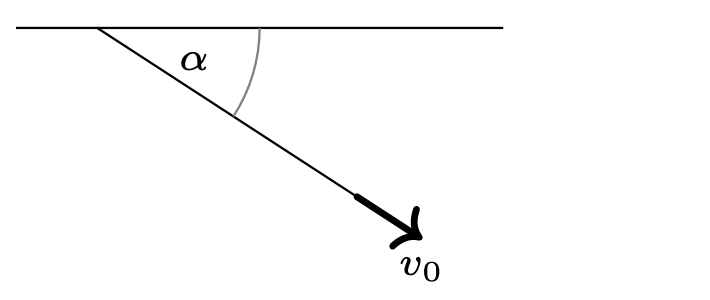
786. Koralik o masie \(M\) może ślizgać się bez tarcia po prostym poziomym pręcie. Do koralika przywiązana jest lekka nierozciągliwa nitka o długości \(l.\) Nitkę ciągniemy za swobodny koniec tak, że jego prędkość przez cały czas skierowana jest wzdłuż nitki i ma wartość \(v_0\) (rys. 3). Jaką siłą ciągniemy w chwili, gdy nitka tworzy z prętem kąt \(\alpha\)? Podczas ruchu nitka znajduje się w płaszczyźnie poziomej.
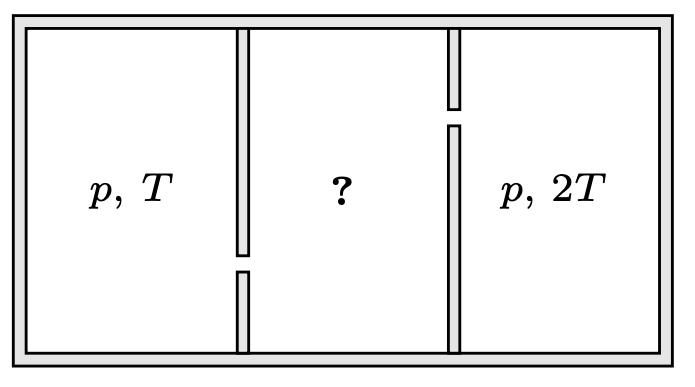
787. Nieprzewodzące ciepła naczynie połączone jest za pomocą dwóch małych jednakowych otworków z dwoma pojemnikami zawierającymi hel w stanie gazowym (rys. 4). W obu pojemnikach podtrzymywane jest jednakowe ciśnienie \(p,\) w jednym z nich podtrzymywana jest temperatura \(T,\) w drugim \(2T.\) Znaleźć ciśnienie i temperaturę w środkowym naczyniu w stanie równowagi.
Rys. 1
Rys. 2
Rys. 3
Rys. 4
Rys. 5
786. Nić jest nierozciągliwa, zatem prędkości wszystkich jej punktów w danej chwili są jednakowe. Gdy kąt między nitką a prętem wynosi \(\alpha ,\) prędkość koralika jest równa \(u={v_0}/{\cos\alpha }.\) Jego przyspieszenie: \[\tag{1} \label{GrindEQ__1_1} a={du}/{dt}=u\tan\alpha {(d\alpha }/{dt)}.\] W małym przedziale czasowym \(\Delta t\) koralik przebywa drogę \(u\Delta t,\) koniec nici przemieszcza się o \(v_0\Delta t\) (rys. 5). Zgodnie z twierdzeniem sinusów \({{u\Delta t}/{\sin(\Delta \alpha )}=l/{\sin\alpha }}.\) Uwzględniając, że kąt \(\Delta \alpha\) jest mały, otrzymujemy \({d\alpha }/{dt}={u\sin\alpha }/{l}\) i zgodnie z \(\eqref{GrindEQ__1_1}\) \(a={{\left(v_0\sin\alpha \right)}^2}/(l\cos^{3}\alpha ).\) Szukana siła, jaką ciągniemy koralik, dana jest wzorem: \[F=Ma/\!\cos\alpha=M(v_{0}\sin\alpha)^{2}/(l\cos^{4}\alpha).\] 787. W stanie równowagi liczba cząsteczek w środkowym naczyniu nie zmienia się, czyli liczby cząsteczek wpadających do tego naczynia w jednostce czasu z lewej i prawej strony oraz opuszczających je są sobie równe: \[\tag{2} \label{GrindEQ__1_} N_1+N_2=N.\] \(N_1\) jest proporcjonalne do liczby cząsteczek w jednostce objętości \(n_1\) w lewym naczyniu oraz do średniej prędkości ich ruchu cieplnego \(v_1,\) która z kolei jest proporcjonalna do \(\sqrt{T}.\) Z równania Clapeyrona \(n_1\sim {p}/{T},\) zatem \({N_1=\alpha {p}/{\sqrt{T}}},\) \(\alpha\) to współczynnik proporcjonalności. Analogicznie \(N_2=\alpha {p}/{\sqrt{2T}},\)
\({N=2\alpha {p_x}/{\sqrt{T_x}}},\) gdzie \(p_x\) jest szukanym ciśnieniem, a \(T_x\) temperaturą w środkowym naczyniu. Podstawiając otrzymane wyrażenia do \(\eqref{GrindEQ__1_}\), otrzymujemy równanie: \[\tag{3} \label{GrindEQ__2_} {p}/{\sqrt{T}}+{p}/{\sqrt{2T}}={2p_x}/{\sqrt{T_x}}.\] W stanie równowagi nie zmienia się również całkowita energia cząsteczek w środkowym pojemniku. Średnia energia przypadająca na cząsteczkę jest proporcjonalna do temperatury, zatem \(N_1T+N_22T=2NT_x,\) \[\tag{4} \label{GrindEQ__3_} p\sqrt{T}+p\sqrt{2T}=2p_x\sqrt{T_x} .\] Rozwiązując układ równań \(\eqref{GrindEQ__2_}\), \(\eqref{GrindEQ__3_}\), otrzymujemy: \[T_x=T\sqrt{2},\ \ \ p_x={p\bigl(\sqrt{2}+1\bigr)}/{2\sqrt[4]{2}}.\]