Zadania z fizyki nr 792, 793
Termin nadsyłania rozwiązań: 30 IV 2025
Redaguje Elżbieta ZAWISTOWSKA
792. \(N=100\) jednakowych kulek o średnicy \(d=0{,}1\) mm znajduje się w ustawionym pionowo cylindrycznym naczyniu o podstawie \(S=1\) m \(^{2}\) pod nieruchomym tłokiem, który znajduje się na wysokości \(h=1\) m. Kulki poruszają się chaotycznie ze średnią prędkością kwadratową \(v_{0}=100\) m/s. Tłok zaczęto podnosić z prędkością \(u=1\) m/s i został on zatrzymany na wysokości \(2h.\) Jaka średnia prędkość kulek ustaliła się po długim czasie? Nie ma strat energii mechanicznej podczas zderzeń, nie uwzględniamy siły grawitacji.
793. Do źródła o sile elektromotorycznej \(U=1{,}5\) V i zaniedbywalnym oporze wewnętrznym dołączono długi łańcuch jednakowych amperomierzy i taką samą liczbę jednakowych woltomierzy (rys. 1). Opór wewnętrzny amperomierza wynosi \(r=1\ \Omega,\) woltomierza 10 k\(\Omega.\) Jakie są wskazania pierwszego i drugiego amperomierza? Ile wynosi suma wskazań wszystkich amperomierzy oraz suma wskazań wszystkich woltomierzy w łańcuchu?
Rys. 1
Rys. 2
Rozwiązania zadań z numeru 10/2024
Przypominamy treść zadań:
784. Szklany pryzmat o małym kącie łamiącym \(\varphi\) umieszczono w pewnej odległości od cienkiej soczewki skupiającej o ogniskowej \(f\) tak, że jedna z powierzchni pryzmatu jest prostopadła do osi optycznej soczewki. Po drugiej stronie soczewki, w jej ognisku znajduje się punktowe źródło światła. Promienie odbite od pryzmatu po załamaniu w soczewce dają dwa obrazy źródła światła oddalone od siebie o \(d.\) Znaleźć współczynnik załamania szkła, z którego wykonano pryzmat.
Musimy rozważyć dwa przypadki:
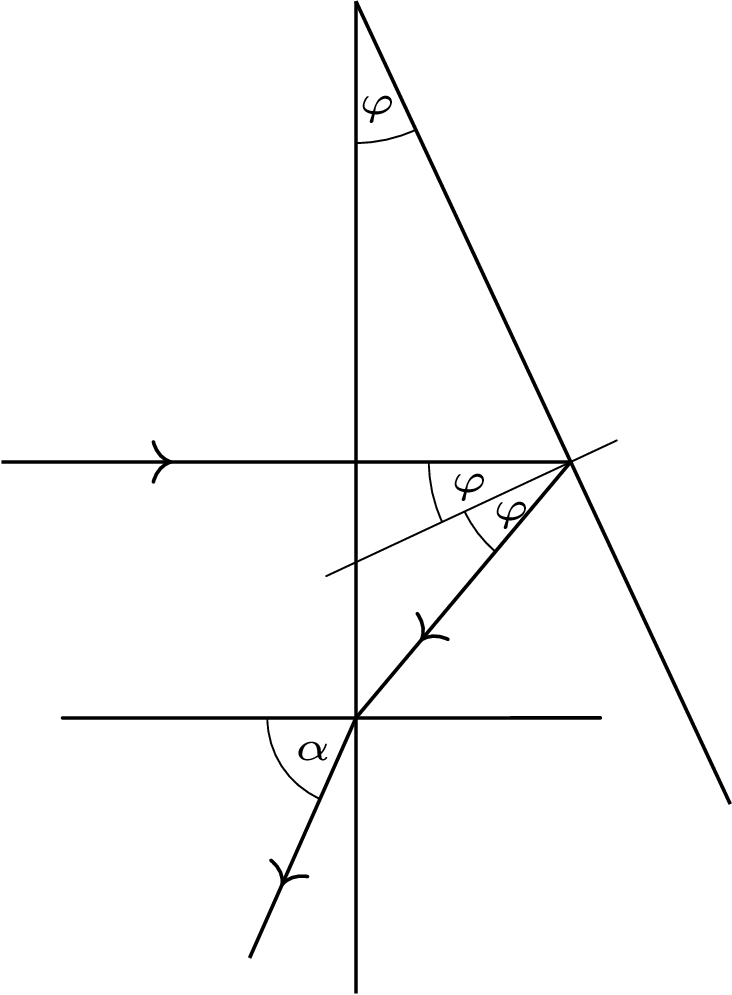
1) Ścianka pryzmatu bliższa soczewki jest prostopadła do jej osi optycznej (rys. 3).
Rys. 3
Równoległa wiązka promieni odbita od bliższej ścianki skupia się w ognisku soczewki, w którym znajduje się źródło. Promienie odbite od dalszej ścianki tworzą po wyjściu z pryzmatu wiązkę nachyloną pod kątem \(\alpha\) do osi optycznej i skupiają się w płaszczyźnie ogniskowej, w odległości \(d=f\operatorname{tg}\alpha\) od ogniska. Z prawa załamania \({\sin\alpha }/{\sin\left(2\varphi \right)}=n.\)
W przybliżeniu małych kątów \(d=f\alpha =2\varphi nf.\)
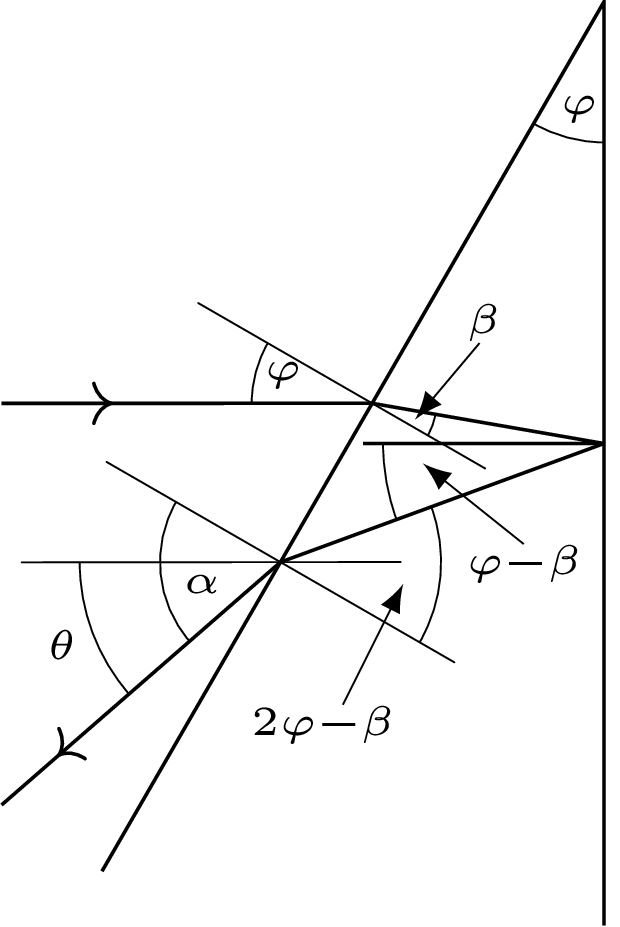
2) Ścianka pryzmatu dalsza od soczewki jest prostopadła do jej osi optycznej (rys. 4).
Rys. 4
Promienie odbite od bliższej ścianki są nachylone do osi optycznej pod kątem \(2\varphi\) i po przejściu przez soczewkę tworzą obraz w płaszczyźnie ogniskowej, oddalonej od ogniska o \(d_1=f\operatorname{tg}\left(2\varphi \right).\) Promienie odbite od dalszej ścianki po wyjściu z pryzmatu tworzą wiązkę odchyloną w drugą stronę o kąt \(\theta =\alpha -\varphi\) i po przejściu przez soczewkę skupiają się w płaszczyźnie ogniskowej w odległości \(d_2=f\operatorname{tg}\theta\) od ogniska. Spełnione są prawa załamania: \({\sin\varphi }/{\sin\beta }=n\) oraz \({\sin \alpha}/{\sin\left(2\varphi -\beta \right)}=n.\) Odległość między obrazami \(d=d_1+d_2.\)
W przybliżeniu małych kątów odległość między obrazami w obu przypadkach jest taka sama, a szukany współczynnik załamania \[n={d}/{\left(2\varphi f\right)}.\]
785. Kondensator płaski, którego powierzchnia okładek jest dużo większa od odległości między nimi, podłączony jest do źródła o sile elektromotorycznej \(\mathcal E\) i umieszczony w jednorodnym polu elektrycznym o natężeniu \(E.\) Linie pola są prostopadłe do powierzchni okładek kondensatora (rys. 2). Jaką pracę trzeba wykonać, aby obrócić ten kondensator o kąt \(\pi\) wokół osi prostopadłej do wektora \(\vec{E}\)?
Wypadkowe pole elektryczne wewnątrz kondensatora przed i po obrocie ma wartość \({\mathcal E }/{d},\) zatem energia pola w tym obszarze nie zmienia się. Zasada zachowania energii w rozważanym procesie ma postać \[% W_1+W_2=0,\] gdzie \(W_1\) jest szukaną pracą sił zewnętrznych, a \(W_2\) pracą źródła. Oznaczając przez \(E_1\) i \(E_2\) wartości pola elektrycznego wytworzonego przez ładunki na kondensatorze odpowiednio przed i po obrocie, a przez \(d\) odległość między okładkami, możemy napisać: \[\mathcal E -E_1d+Ed=0,\ \ \ \mathcal E -E_2d-Ed=0,\] stąd \(E_1={\mathcal E }/{d}+E,\) \(E_2={\mathcal E }/{d}-E.\)
Ładunki na okładkach o powierzchni \(S\) połączonych z dodatnim biegunem źródła przed i po obrocie wynoszą odpowiednio: \[Q_1={\varepsilon }_0S\left({\mathcal E }/{d}+E\right),\ \ \ Q_2={\varepsilon }_0S\left({\mathcal E }/{d}-E\right).\] Podczas obrotu z okładki dodatniej odpływa ładunek \(\Delta Q=Q_1-Q_2=2{\varepsilon }_0SE,\) a praca źródła jest ujemna: \(W_2=-2{\varepsilon }_0E\mathcal E .\) Szukana praca sił zewnętrznych wynosi \[W_1=2{\varepsilon }_0SE\mathcal E .\]
Czołówka ligi zadaniowej Klubu 44 F po zakończeniu roku szkolnego 2023/24 i po sprawdzeniu zadań 780 (\(WT = 3{,}01\)), 781 (\(WT = 3{,}31\))
Paweł Perkowski Ożarów Maz. 5 – 43,19 Konrad Kapcia Poznań 2 – 42,29 Jacek Konieczny Poznań 40,87 Tomasz Wietecha Tarnów 17 – 34,38 Andrzej Nowogrodzki Chocianów 3 – 27,49 Jan Zambrzycki Białystok 4 – 26,81 Paweł Kubit Kraków 17,21 Krzysztof Magiera Łosiów 4 – 13,42 Piotr Adamczyk Bydgoszcz 2 – 9,03 Ryszard Baniewicz Włocławek 2 – 7,91 Michał Koźlik Gliwice 5 – 6,54 Piotr Łaba Biłgoraj 6,36 Sławomir Buć Mystków 1 – 5,51 Marian Łupieżowiec Gliwice 3 – 4,25 Leon Charkiewicz Koszalin 3,85 Tomasz Rudny Poznań 1 – 3,34 Hubert Pochłopień Toruń 1,1 Wiktor Garczyński 0,66 Lista obejmuje uczestników ligi, którzy przysłali rozwiązanie co najmniej jednego zadania z rocznika 2022, 2023 lub 2024.
Podsumowanie ligi zadaniowej Klubu 44 F w roku szkolnym 2023/2024
Dziewięć zadań z omawianego okresu uzyskało współczynnik trudności większy od trzech, a pięć mniejszy od dwóch.
Nikt nie rozwiązał poprawnie zadania 774 (\(WT = 3{,}88\)), gdzie należało znaleźć gęstość klocka w stanie równowagi trwałej, zanurzonego w wodzie tak, że jego powierzchnia boczna jest równoległa do powierzchni cieczy. Zadanie było dosyć pracochłonne i część uczestników nadesłało rozwiązania jedynie drugiego zadania z tej serii, co wpłynęło na jego współczynnik trudności. Nikt nie podjął próby rozwiązania sposobem „firmowym”, polegającym na zbadaniu momentów sił działających na klocek przy małym odchyleniu z położenia równowagi. Zaproponowane zostało porównanie położenia środków ciężkości klocka w różnych stanach równowagi, ale nie uwzględniono faktu, że podczas zanurzenia klocka przemieszczamy na powierzchnię wodę, której miejsce zajmuje zanurzona część klocka.
Maksymalnej możliwej oceny nie uzyskało żadne z rozwiązań zadania 776 (\({WT = 3{,}56}\)). Koralik przymocowany do ustawionej pionowo obręczy za pomocą dwóch jednakowych poziomych sprężyn odchylono od położenia równowagi wzdłuż średnicy i puszczono. Zakładając brak poślizgu, należało znaleźć przyspieszenie obręczy w chwili początkowej. Jeden z uczestników podał dwa rozwiązania tego zadania. Jedno, w którym zastosował równania Lagrange’a, było poprawne. W drugim wykorzystał prawa ruchu obrotowego, zakładając, że obręcz i kulka tworzą jedną bryłę sztywną. Dodatkowy błąd spowodował, że wyniki obu rozwiązań były zgodne. Błąd polegający na założeniu, że obręcz i kulka mają jednakowe przyspieszenia, pojawił się też w kilku innych rozwiązaniach.
W zadaniu 781 (\(WT = 3{,}31\)) początkowo nieruchoma, naładowana cząstka poruszała się w polu nieruchomej cząstki naładowanej przeciwnie oraz w jednorodnym polu magnetycznym prostopadłym do linii łączącej cząstki w chwili początkowej. Znając minimalną odległość między cząstkami, należało znaleźć wartość wektora indukcji pola magnetycznego. Najwyżej ocenione zostało rozwiązanie Konrada Kapci, chociaż nie była to ocena maksymalna. Wypisał on równania ruchu cząstki we współrzędnych kartezjańskich, rozważył przypadki o innych warunkach początkowych i wykorzystując analizę numeryczną, zgadł poprawne rozwiązanie.
Zgodnie z tradycją trudności sprawiały zadania z termodynamiki. Nikt nie rozwiązał w pełni poprawnie zadania 779 (\(WT = 3{,}15\)), gdzie w izolowanym cieplnie naczyniu tłok był bardzo szybko podnoszony, a po ustaleniu się równowagi swobodnie opadał. Oba procesy nie były kwazistatyczne i należało korzystać z zasady zachowania energii, podczas gdy uczestnicy albo w jednym, albo w drugim procesie korzystali z równania \(pV^{c_{p}/c_{v}}=\textup{const}.\) Podobnie było z zadaniem 770 (\(WT = 3{,}5\)), w którym opróżnione i izolowane cieplnie naczynie zapełniane było szybko przez gaz z otoczenia. Jako jedyny poprawnie rozwiązał to zadanie Tomasz Wietecha.
T. Wietecha był też jedynym autorem ocenionego na jedynkę rozwiązania zadania 765 (\(WT = 3{,}4\)). Należało w nim znaleźć okres małych drgań obręczy nałożonej na poziomy nieruchomy walec, przy braku poślizgu między walcem i obręczą.
Zadanie 762 (\(WT = 3{,}01\)) bezbłędnie rozwiązał Ryszard Baniewicz. Pytanie było o minimalną energię fotonu potrzebną do utworzenia pary elektron-pozyton w pobliżu spoczywającego elektronu. Zadanie 766 (\(WT = 3{,}06\)) dotyczyło oddziaływania połówek równomiernie naładowanej, nieprzewodzącej kuli. Jedynki otrzymali Paweł Perkowski i Tomasz Wietecha. W zadaniu 780 (\(WT = 3{,}01\)) rozważane było niesprężyste zderzenie kulek zawieszonych na jednakowych niciach. Bezbłędne rozwiązania przysłali Marian Łupieżowiec i Tomasz Wietecha.
Za rozwiązania tegorocznych zadań najwięcej jedynek zdobył Tomasz Wietecha (11), drugie miejsce zajął Ryszard Baniewicz, trzecie Paweł Perkowski. Tomasz Rudny został w tym roku członkiem klubu 44 F, przekraczając granicę 44 punktów, Ryszard Baniewicz przekroczył ją po raz drugi, Marian Łupieżowiec po raz trzeci, a Tomasz Wietecha siedemnasty!
Ciekawostką jest, że o rozwiązanie zadania 763 (\(WT =2{,}46\)) z mechaniki punktu materialnego, za które maksymalne oceny otrzymały trzy osoby, jeden z uczestników poprosił sztuczną inteligencję, której wysiłek zakończył się niepowodzeniem. Zdecydowanie odradzam dalsze takie eksperymenty, bo nie o to w tej zabawie chodzi.
Zadania z matematyki nr 895, 896
Termin nadsyłania rozwiązań: 30 IV 2025
Redaguje Marcin E. KUCZMA
895. Na okręgu zaznaczono \(n\) punktów; \({n\ge3}\) jest ustaloną liczbą nieparzystą. Każdemu punktowi została przyporządkowana wartość 0 lub 1. Dozwolone są ruchy polegające na wybraniu trzech kolejnych punktów o wartościach (kolejno) \(a,b,c\) takich, że \({a=c},\) i zamianie \(b\) na \(1{-}b.\) Udowodnić, że startując z dowolnej konfiguracji i wykonując dozwolone ruchy, można uzyskać jednakową wartość dla wszystkich \(n\) punktów.
896. Udowodnić, że ciąg \((A_1,A_2,A_3,\ldots)\) o wyrazach \[A_n={1\over n}\sum\limits_{k=1}^{2^n}{1\over k}\] jest malejący.
Zadanie 896 zaproponował pan Jerzy Cisło z Wrocławia
Lista uczestników ligi zadaniowej
Klub 44 M
po zakończeniu sezonu
(roku szkolnego) 2023/24
Legenda (przykładowo):
stan konta 9–40,58 oznacza, że uczestnik już dziewięciokrotnie zdobył 44 punkty, a w kolejnej (dziesiątej) rundzie ma 40,58 punktów.Zestawienie obejmuje wszystkich uczestników ligi, którzy spełniają następujące dwa warunki:
– stan ich konta (w aktualnie wykonywanej rundzie) wynosi co najmniej 12 punktów;
– przysłali rozwiązanie co najmniej jednego zadania z rocznika 2022, 2023 lub 2024.
Nie drukujemy więc nazwisk tych uczestników, którzy rozstali się z ligą trzy lata temu (lub dawniej); oczywiście jeśli ktokolwiek z nich zdecyduje się wrócić do naszych matematycznych łamigłówek, jego nazwisko automatycznie wróci na listę. Serdecznie zapraszamy!
Rozwiązania zadań z numeru 10/2024
Przypominamy treść zadań:
887. Znaleźć najmniejszą liczbę rzeczywistą \(A,\) dla której istnieją liczby zespolone \(u,v,w\) oraz liczba rzeczywista \(B\) takie, że \({|u|=|v|=|w|=1=uvw},\) zaś \({u+v+w=A+Bi}.\)
Prościej: chodzi o wyznaczenie minimalnej wartości \({{\rm{Re}}(u+v+w)}\) dla liczb \(u,v,w\) o podanych własnościach. Są to liczby o module 1, zatem istnieją liczby rzeczywiste \(x,y,z\) takie, że \({u={\rm{e}}^{ix}},\) \({v={\rm{e}}^{iy}},\) \({w={\rm{e}}^{iz}}.\) Warunek \({uvw=1}\) oznacza, że \({x+y+z=2k\pi}\) (\({k\in{\mathbb{Z}}}\)). Przy tym \[{\rm{Re}}(u+v+w)={\rm{Re}}(u)+{\rm{Re}}(v)+{\rm{Re}}(w)=\cos{x}+\cos{y}+\cos{z}.\] Należy znaleźć minimum tej sumy przy powyższym warunku.
Niech \({c=\cos{x+y\over 2}}\); więc \({\cos{x}+\cos{y}=2\cos{x+y\over 2}\cos{x-y\over 2}\ge-2|c|}\); a skoro \({z=2k\pi-(x+y)},\) zatem \({\cos{z}=\cos\bigl(2\cdot{x+y\over 2}\bigr)=2c^2-1}.\) W konsekwencji \[\textstyle \cos{x}+\cos{y}+\cos{z}\ge2c^2-2|c|-1=2\bigl(|c|-{1\over 2}\bigr)^2-{3\over 2}\ge-{3\over 2}\,.\] W tych szacowaniach zachodzi równość, gdy \({x=y=z=\pm{2\over 3}\pi}\) (co odpowiada liczbom \({u=v=w=\cos({2\over 3}\pi)\pm{i\,\sin({2\over 3}\pi)}}\,\)). Szukane minimum wynosi więc \(-{3\over 2}.\)
888. Znaleźć wszystkie trójki liczb całkowitych \({x,y,z\ge0}\) spełniające równanie \({7^x+2^{x+y}=z^2}.\)
Niech liczby \({x,y\ge0},\) \({z>0}\) spełniają zadane równanie. Gdy \({x=0},\) wtedy \({2^y=(z-1)(z+1)},\) więc \({z\pm1}\) to potęgi dwójki, skąd \({z=3}\) i \({y=3}.\) Trójka \((0,3,3)\) jest jednym z rozwiązań.
Gdy \({x=1},\) równanie ma postać \({7+2^{y+1}=z^2},\) więc \(z\) jest liczbą nieparzystą. Dostajemy \({2^{y+1}\equiv2}\) (mod 4), czyli \({y=0}\); wtedy \({z=3}.\) Trójka \((1,0,3)\) jest jednym z rozwiązań.
Dalej rozważamy \({x\ge2}.\) Dane równanie pokazuje, że \({3^x\equiv{z^2}}\) (mod 4), co jest możliwe tylko dla parzystego \(x.\) Niech więc \({x=2t}\) (\({t\ge1}\)); zapiszmy równanie tak: \({(z+7^t)(z-7^t)=2^{2t+y}}.\) Pierwszy czynnik po lewej stronie jest liczbą dodatnią, więc drugi też; stąd \({z\ge8}.\) Oba czynniki muszą być potęgami dwójki: \[z+7^t=2^k,\ \ \ z-7^t=2^l\ \ \ (k>l\ge0,\;\;k+l=2t+y).\] Po odjęciu stronami: \({2\cdot7^t=2^l(2^{k-l}-1)},\) skąd \({l=1},\) \({7^t=2^{k-1}-1}.\)
Gdy \(k=4,\) dostajemy \(t=1\) (czyli \(x=2\)), \(y=k+l-2t=3,\) \(z^2=7^2+2^5,\) czyli \(z=9.\) Trójka \((2,3,9)\) jest jednym z rozwiązań. Gdy \({k\ge5},\) dostajemy \({7^t=2^{k-1}-1\equiv-1}\) (mod 16). Sprzeczność, bo potęgi siódemki (mod 16) to tylko 1 lub 7. Zadane równanie ma więc trzy rozwiązania: \((0,3,3),\) \((1,0,3),\) \((2,3,9).\)
Podsumowanie ligi zadaniowej Klubu 44 M w roku szkolnym 2023/2024
Teraz coroczne omówienie wybranych zadań – czyli (jak zwykle) tych, które okazały się trudniejsze: wysoki współczynnik trudności (\(WT\)) i/lub niewielka liczba poprawnych rozwiązań (\(LPR\)); oraz tych, w których pojawiły się intrygujące pomysły rozwiązań oraz komentarze uczestników. Znaczne ich fragmenty umieszczamy w e-wydaniu (w zakładce ,,Załącznik do elektronicznego omówienia ligi matematycznej”).
\(*\ \ \ *\ \ \ *\)
Zadanie 866. [Dane \({p,q\in{\mathbb{P}}}\) (zbiór liczb pierwszych), \({p\ne{q}}\); \({2^p{-}1,2^q{-}1\in{\mathbb{P}}}\); \({pq|2^p{-}1},\) \({pq|2^q{-}1}\); \({d\in\mathbb N},\) \({d|2^{pq}{-}1}\) \(\Rightarrow\) \({pq|d{-}1}\)] (\(WT\) = 2,68; \(LPR\) = 9). Wszystkie dobre rozwiązania podobne (zasadniczo jak firmowe): M. Adamaszek, W. Bednarek, S. Kitowski, K. Maziarz, J. Olszewski, M. Pater, M. Warmuz, T. Wietecha, P. Wiśniewski.
Weterani Klubu 44 M
(w kolejności uzyskiwania
statusu weterana):
J. Janowicz (8), P. Kamiński (5), M. Gałecki (5), J. Uryga (4), A. Pawłowski (4), D. Sowizdrzał, T. Rawlik (6), M. Mazur, A. Bonk, K. Serbin, J. Ciach (5), M. Prauza (4), P. Kumor (16), P. Gadziński (7), K. Jedziniak, J. Olszewski (24), L. Skrzypek (4), H. Kornacki, T. Wietecha (14), T. Józefczyk, J. Witkowski (5), W. Bednorz, B. Dyda (5), M. Peczarski, M. Adamaszek (9), P. Kubit (8), J. Cisło (17), W. Bednarek (9), D. Kurpiel, P. Najman (9), M. Kieza (4), M. Kasperski (5), K. Dorobisz, A. Woryna (4), T. Tkocz, Z. Skalik (4), A. Dzedzej, M. Miodek, M. Małogrosz (4), K. Kamiński, J. Fiett (4), M. Spychała (5), A. Kurach, S. Bednarek, M. Pater, Ł. Merta
(jeśli uczestnik przekroczył barierę 44 punktów więcej niż trzy razy, sygnalizuje to liczba w nawiasie).
Pozostali członkowie Klubu 44 M
(alfabetycznie):
,,dwukrotni”: Z. Bartold, A. Czornik, A. Daniluk, Z. Galias, Ł. Garncarek, J. Garnek, A. Idzik, P. Jędrzejewicz, G. Karpowicz, H. Kasprzak, T. Komorowski, Z. Koza, J. Łazuka, J. Małopolski, J. Mikuta, E. Orzechowski, R. Pagacz, K. Patkowski, K. Pióro, F. S. Sikorski, J. Siwy, R. Słowik, S. Solecki, T. Warszawski, G. Zakrzewski, B. Żmija;
,,jednokrotni”: R. M. Ayoush, T. Biegański, W. Boratyński, P. Burdzy, T. Choczewski, M. Czerniakowska, P. Duch, P. Figurny, M. Fiszer, L. Gasiński, A. Gluza, T. Grzesiak, K. Hryniewiecki, K. Jachacy, M. Jastrzębski, P. Jaśniewski, A. Jóźwik, J. Klisowski, J. Kraszewski, A. Krzysztofowicz, R. Kujawa, T. Kulpa, A. Langer, R. Latała, P. Lipiński, P. Lizak, P. Łabędzki, M. Łupieżowiec, W. Maciak, J. Mańdziuk, B. Marczak, M. Marczak, M. Matlęga, K. Matuszewski, K. Maziarz, R. Mazurek, H. Mikołajczak, M. Mikucki, J. Milczarek, R. Mitraszewski, K. Morawski, M. Mostowski, W. Nadara, W. Olszewski, R. Pikuła, B. Piotrowska, W. Pompe, N. Porwol, M. Roman, M. Rotkiewicz, A. Ruszel, Z. Sewartowski, A. Smolczyk, P. Sobczak, Z. Surduka, T. Szymczyk, W. Szymczyk, W. Tobiś, K. Trautman, P. Wach, J. Węgrecki, P. Wiśniewski, K. Witek, A. Wyrwa, M. Zając, Z. Zaus, K. Zawisławski, K. Zygan, P. Żmijewski.
Zadanie 869. [Dla \({x,y\in{\mathbb{R}}_+}\): \({g(x,y)=\min\Bigl(x,\,{1\over x},\,{xy+1\over x}\,\bigr)}\); \({\sup{g(x,y)}=?}\)] (\(WT\) = 1,34; \(LPR\) = 25). Jak widać, było łatwe. Przywołujemy je tu po to, by wspomnieć o kilku rozwiązaniach niepoprawnych, korzystających z ,,twierdzenia” (fałszywego): Jeśli funkcja ciągła na pewnym zbiorze \({A\subset{\mathbb{R}}^n}\) jest w jego wnętrzu różniczkowalna, ale bez punktów, w których różniczka jest zerowa, wówczas wartość minimalna jest przyjmowana w pewnym punkcie brzegu zbioru \(A.\) No cóż, tak jest, gdy zbiór \(A\) jest domknięty i ograniczony. Ale gdy (na przykład) \(A\) jest ćwiartką płaszczyzny (\({x\ge0},\) \({y\ge0}\)), wystarczy spojrzeć na funkcję \({\rm{e}}^{-xy},\) by zrozumieć błąd.
Zadanie 870. [\(\triangle{ABC}\) równoboczny \(\Rightarrow\) (a ) \(\forall\,P\in\hbox{pł}(ABC)\colon\,\newline AP+BP\ge{CP}\) (\({\&\hbox{cykl}}\)); (b ) to samo \(\forall\,P\) w przestrzeni] (\(WT\) = 2,50; \(LPR\) = 13). Redaktor Ligi ze skruchą przyznaje, że nie rozpoznał tu szczególnego przypadku nierówności Ptolemeusza (\({PA\cdot{BC}+PB\cdot{AC}\ge{PC}\cdot{AB}},\) słusznej dla dowolnej czwórki punktów w przestrzeni dowolnego wymiaru – rozwiązanie w jednej linijce, dostrzeżone przez ośmioro uczestników: M. Adamaszek, B. Knapik, P. Kubit, P. Kumor, K. Maziarz, B. Mroczek, T. Wietecha, P. Wiśniewski.
Piękne rozwiązanie czysto geometryczne, dwoma sposobami w części (a ) i dwoma w części (b ), przedstawił Janusz Olszewski. Oto jeden z tych sposobów (b ): niech (b.s.o.) \({P\ne{A}},\) \({AB=BC=CA=a}\); \(B',C',P'\) – obrazy \(B,C,P\) w inwersji względem sfery o środku \(A,\) promieniu 1; nietrudno wykazać podobieństwa \({\triangle{ABP}\sim\triangle{AP'B'}},\) \({\triangle{ACP}\sim\triangle{AP'C'}},\) \({\triangle{ABC}\sim\triangle{AC'B'}}\); a stąd, pisząc odpowiednie proporcje, wywnioskować, że \(\triangle{B'P'C'}\) jest podobny do trójkąta o bokach \(BP,\) \(CP,\) \(AP\) (!) (całość pracy w e-wydaniu).
Zadanie 871. [Dana liczba parzysta \({n>0}\); (a ) \({P\colon=[n{+}1,2n{+}1]\cap\mathbb N}\) \(\Rightarrow\) \({\exists\,M\subset{P}\,\forall\,m\in{M}\colon\,\sum_{k\in{M}}k\not\equiv 0}\) (mod \(m\)); (b ) czy zawsze istnieją dwa różne takie zbiory \(M\)?] (\(WT\) = 1,99; \(LPR\) = 16). Niech \({S=\sum_{k=n+1}^{2n+1}k=cd},\) gdzie \({c=n+1},\) \({d={3\over 2}n+1}.\) Janusz Olszewski traktuje liczby \(n{+}1,\ldots,2n{+}1\) jako wierzchołki grafu skierowanego, w którym \({(x\to{y})\Leftrightarrow(y|S{-}x)}.\) Załóżmy odpowiedź nie na pytanie (b ); wtedy musi istnieć \(n\) wierzchołków, z których wychodzą krawędzie do innych wierzchołków; więc istnieje \({{}\ge{n}}\) krawędzi \({x\to{y}},\) gdzie \({x\ne{y}}.\) Łatwo sprawdzić, że \({c\to{c}},\) \({d\to{d}},\) zatem istnieje \({{}\ge{n+2}}\) krawędzi wchodzących do \({n+1}\) wierzchołków; pewne dwie muszą wchodzić do tego samego: \({k\to{m}},\) \({l\to{m}}\) (\({k\ne{l}}\)). To oznacza, że \({m|S{-}k},\) \({m|S{-}l},\) skąd \({m|k{-}l}\); to już sprzeczność, bo \({|k-l|\le{n}<m}.\) Stąd odpowiedź tak na pytanie (b ) (więc i dowód tezy (a )).
Kilka prac zawiera zasadniczo takie samo rozumowanie, jednak bez terminologii ,,grafy, krawędzie”, która tu wydaje się idealnie dopasowana.
W dwóch innych pracach (M. Kasperski, B. Knapik) widzimy ciekawe symulacje komputerowe (\(\to\) e-wydanie) sugerujące, że zbiorów o badanej własności jest znacznie więcej niż dwa.
Zadanie 875. [Dana liczba nieparzysta \(N\) oraz ciąg \((x_1,\ldots,x_N),\) \({x_i\in\{0,1\}}\); dla \({k\in\{1,\ldots,N\}}\): \({a_k\colon\,=\sum_{i<k}x_i},\) \({b_k\colon\,=\sum_{i>k}(1{-}x_i)},\) \({c_k=a_k+b_k}\); \({\exists!\,z\colon\,|\{k\colon\,z=c_k\}|\equiv 1}\) (mod 2); \({z=?}\)] (\(WT\) = 2,62; \(LPR\) = 7 (8?)). Dobre rozwiązania (w większości podobne do firmowego): M. Adamaszek, R. Kujawa, J. Olszewski, M. Warmuz, M. Kasperski, P. Łabędzki, M. Spychała; ponadto jedna praca z pomyłką (której usunięcie nie jest trudne, jednak wymaga małej zmiany rozumowania).
Zadanie 878. [Znaleźć \({r\in\mathbb N},\) \({r>2}\): \(\exists\) nieskończenie wiele zbiorów \(\{p_1,\ldots,p_r\},\) \({p_i\in{\mathbb{P}}}\): \({\forall\,i\in\{1,\ldots,r\}\colon}\) \({p_1\ldots{p_r}|2^{p_i-1}-1}\) (im większe \(r,\) tym lepiej)] (\(WT\) = 3,29; \(LPR\) = 3+autor). Zaczniemy od \({r=3}.\) Ładne rozwiązanie pokazał Janusz Olszewski (przejrzysta redakcja – zachęcamy do lektury w e-wydaniu!). Inną drogą poszedł Piotr Wiśniewski, odwołując się do pracy A. Rotkiewicza z roku 1967 (w której jedno z twierdzeń nakrywa naszą tezę dla \({r=3}\)); nie podał pełnego odsyłacza. Dla zainteresowanych Czytelników: (przyp. red.: praca, zatytułowana On the prime factors of the number \(2^{p-1}{-}1\) , ukazała się w Glasgow Math.J. 9 (1968), 82–86; natomiast w Cambridge Univ. Press – jej przedruk, który łatwo wyszukać – wystarczy wstukać np. on the prime factors rotkiewicz; podany tam dowód nie jest elementarny, przy tym odsyła do jeszcze innych prac).
Przypadek \({r=2}\) był rozpatrzony w zadaniu z obozu OM 2010 (om.sem.edu.pl; ten odsyłacz posłużył jako wskazówka do omawianego zadania 878). Piotr Kumor (autor 878) zauważył, że przez dość naturalną modyfikację daje się uzyskać tezę dla \({r=4}.\) Uzyskana przez autora konstrukcja została użyta jako rozwiązanie firmowe. Dokładnie tę samą konstrukcję znalazł Michał Adamaszek. Co ciekawe, obaj Panowie opatrzyli swoje prace komentarzami, w znacznej mierze identycznymi. Zamieszczamy je w e-wydaniu; kto ciekawy, co to Super-Poulet numbers, niech tam zajrzy. Warto!
Autor zadania liczył, że od rozwiązujących dowie się czegoś na temat możliwości \({r>4}\); niestety, \({r=4}\) pozostaje (na razie?) osiągnięciem max.
Zadanie 880. [Czy istnieją \({A,B\subset{\mathbb{Q}}_+}\) takie, że: \({A\cap{B}=\emptyset},\) \({A\cup{B}={\mathbb{Q}}_+}\) oraz (dla \({x,y\in{\mathbb{Q}}_+}\)): \({\bigl(xy=1\,\Rightarrow\,x,y\;\hbox{są w~tym samym zbiorze ($A$~lub~$B$)}\bigr)}\); \({\bigl(|x{-}y|=1\,\Rightarrow\,x,y\;\hbox{są w~różnych zbiorach}\bigr)}\)?] (\(WT\) = 1,63; \(LPR\) = 16). Michał Adamaszek dał rozwiązanie – wzorzec zwięzłości: każda liczba \({x\in{\mathbb{Q}}_+}\) ma jednoznaczne rozwinięcie w skończony ułamek łańcuchowy \({x=[a_0;\,a_1,\ldots,a_n]}\) (notacja: np. \({[a_0;\,a_1,a_2,a_3]=a_0+{1\over a_1+{1\over a_2+{1\over a_3}}}}\,\)): \({a_0\ge0},\) \({a_i\ge1}\) dla \({i\ge1}\); \({a_n\ge2}\) jeśli \({n\ge1}.\) Przypisujemy \(x\) do zbioru \(A\) (odp. \(B\)), gdy suma \({\sum_{i=0}^na_i}\) jest parzysta (odp. nieparzysta). Tak określone zbiory \(A,B\) spełniają wymagane warunki, co wynika z równości \({1\over x=[0;\,a_0,a_1,\ldots,a_n]},\) \({x-1=[a_0{-}1;\,a_1,\ldots,a_n]}\) (dla \({x>1}\)).
To samo rozumowanie podali: Andrzej Daniluk i Piotr Kumor. W pozostałych pracach nie ma mowy o ułamkach łańcuchowych, choć de facto są one ,,w tle” obecne (czymże innym jest ,,uogólniony algorytm Euklidesa”?) – brak tych kluczowych słów sprawia, że zapis staje się cięższy (vide: firmówka). Odnotujmy ponadto jedno rozwiązanie wyraźnie odmienne (bardziej kombinatoryczne): Janusz Olszewski ( \(\to\) e-wydanie).
Zadanie 881. [\({a_0=3},\) \({a_{n+1}=a_n^2-2}\); \({\lim_{n\to\infty}(a_1\ldots{a_{n-1}}/{a_n})=}\) ?] (\(WT\) = 1,50; \(LPR\) = 18). Nie sprawiło kłopotu uczestnikom; wielu z nich znalazło nie tylko wynik \({1/\sqrt5},\) ale również wartość badanej granicy \({1/\sqrt{a_0^2-4}}\) przy innych wartościach początkowych \({|a_0|>2}.\) Znacznie ciekawsze jest rozważanie przypadku \({|a_0|\le2}\) (co nie było przedmiotem zadania; a szkoda); granica wówczas nie istnieje, co wnikliwie uzasadnił Janusz Olszewski (\(\to\) e-wydanie).
Zadanie 882. [\(ABCD\) – równoległobok; \(K,L,M,N\) – punkty wewnątrz boków \(AB,\) \(BC,\) \(CD,\) \(DA\) \(\Rightarrow\) (a) ortocentra trójkątów \({ANK,BKL,CLM,DMN}\) tworzą równoległobok; (b) to samo dla ich środków ciężkości; (c) to samo dla środków okręgów opisanych] (\(WT\) = 2,27; \(LPR\) = 12). Efektowne ,,dynamiczne” rozumowanie przeprowadził Janusz Fiett. Własności (a), (b), (c) są oczywiste, gdy \(K,L,M,N\) są środkami odpowiednich boków (cała konfiguracja jest wówczas środkowo symetryczna). A dalej – jeden wspólny pomysł daje uzasadnienie tych trzech tez; dla przykładu weźmy własność (c): załóżmy, że dla pewnego wyboru punktów \(K,L,M,N\) czworokąt \(A'B'C'D'\) (o wierzchołkach w środkach okręgów opisanych na wymienionych trójkątach) jest równoległobokiem. Wybieramy jeden z tych punktów – powiedzmy \(M\) – i przesuwamy go do innego położenia na boku \(CD,\) nie ruszając przy tym punktów \(N,K,L\); punkty \(A',B'\) nie ruszają się; proste symetralne odcinków \(CL\) i \(DN\) również nie zmieniają położenia; zaś proste symetralne odcinków \(CM\) i \(DM\) przesuwają się równolegle, przy czym odległość między nimi pozostaje stała (równa \({1\over 2}CD\)). Odcinek \(C'D'\) (wyznaczony przez odpowiednie punkty przecięcia jednej pary symetralnych z drugą parą) wykonuje przesunięcie równoległe (!), wobec czego czworokąt \(A'B'C'D'\) (przy nowym położeniu punktów \(C',D'\)) nadal jest równoległobokiem. Wystarczy teraz wykonać analogiczne przemieszczenia punktów \({N\in{DA}},\) \({K\in{AB}},\) \({L\in{BC}}\) do dowolnie wybranych pozycji; \(A'B'C'D'\) pozostanie równoległobokiem.
W przypadku każdej z własności (a), bądź (b), przesunięcie punktu \({M\in{CD}}\) (bez ruszania \(N,K,L\)) daje podobny efekt: można wskazać dwie pary prostych równoległych, których odpowiednie przecięcia wyznaczają punkty \(C',D',\) określone teraz jako ortocentra bądź środki ciężkości trójkątów \(CLM,\) \(DMN\); przy tym jedna para pozostaje nieruchoma, a druga przesuwa się równolegle, nie zmieniając odległości, dzięki czemu odcinek \(C'D'\) znów się przesuwa równolegle; konkluzja jak w przypadku (c). Wskazanie owych par prostych zostawiamy Czytelnikowi jako nietrudne ćwiczenie; a kto woli przyjść na gotowe – może zajrzeć do e-wydania, gdzie znajdzie omawiane rozwiązanie bez skrótów.