Zadania z matematyki nr 889, 890
Redaguje Marcin E. KUCZMA
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
879 (\(WT = 1{,}59\)) i 880 (\(WT = 1{,}63\))
z numeru 4/2024
Łukasz Merta Kraków 47,14 Szymon Kitowski Warszawa 41,11 Adam Woryna Ruda Śl. 40,91 Michał Adamaszek Kopenhaga 39,12 Witold Bednarek Łódź 37,29 Krzysztof Zygan Lubin 36,06 Andrzej Daniluk Warszawa 32,96 Mikołaj Pater 32,57 Jędrzej Biedrzycki 32,29 Tomasz Wietecha Tarnów 31,41 Andrzej Kurach Ryjewo 30,66 Pan Łukasz Merta dołączył do grona Weteranów, zaliczając trzecie okrążenie.
889. Ciąg \((a_1,\ldots,a_N),\) długości \(N,\) ma wyrazy \({a_k\in\{2,3,5\}},\) z sumą \({a_1+\ldots+a_N=A}.\) Niech \({b_k=a_ka_{k+1}a_{k+2}a_{k+3}}\) (gdzie, cyklicznie, \({a_{N+i}=a_i}\)). Zakładamy, że każda z liczb \({b_1,\ldots,b_N}\) dzieli się przez \(30.\) Przyjmując jako znane wartości \(N,\) \(A\) (dla których istnieje co najmniej jeden ciąg \((a_k)\) o podanych własnościach) wyznaczyć wszystkie możliwe wartości sumy \({B=b_1+\ldots+b_N}.\)
890. W czworokącie wypukłym \(ABCD\) przekątne przecinają się w punkcie \(P\); boki \(BC\) i \(DA\) nie są równoległe, a ich symetralne przecinają się w punkcie \(Q\) (różnym od \(P\)), leżącym wewnątrz czworokąta. Trójkąty \(BQC\) i \(DQA\) są podobne. Udowodnić, że prosta \(PQ\) zawiera dwusieczne kątów \(APB\) i \(CPD.\)
Zadanie 890 zaproponował pan Wojciech Maciak z Warszawy.
Zadania z fizyki nr 786, 787
Redaguje Elżbieta ZAWISTOWSKA
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
776 (\(WT=3{,}56\)), 777 (\(WT=2{,}59\)) z numeru 4/2024
Jacek Konieczny Poznań 40,87 Paweł Perkowski Ożarów Maz. 5–39,93 Konrad Kapcia Poznań 2–39,58 Tomasz Wietecha Tarnów 17–26,54 Andrzej Nowogrodzki Chocianów 3–25,24 Jan Zambrzycki Białystok 4–23,88 Termin nadsyłania rozwiązań: 31 I 2025
 Rys. 1
Rys. 1
786. Koralik o masie \(M\) może ślizgać się bez tarcia po prostym poziomym pręcie. Do koralika przywiązana jest lekka nierozciągliwa nitka o długości \(l.\) Nitkę ciągniemy za swobodny koniec tak, że jego prędkość przez cały czas skierowana jest wzdłuż nitki i ma wartość \(v_0\) (rys. 1). Jaką siłą ciągniemy w chwili, gdy nitka tworzy z prętem kąt \(\alpha\)? Podczas ruchu nitka znajduje się w płaszczyźnie poziomej.
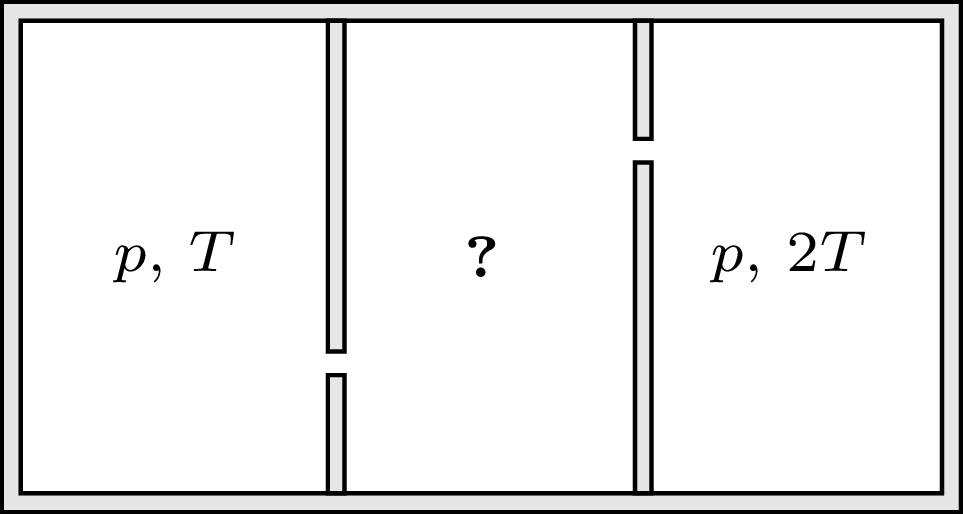
 Rys. 2
Rys. 2
787. Nieprzewodzące ciepła naczynie połączone jest za pomocą dwóch małych jednakowych otworków z dwoma pojemnikami zawierającymi hel w stanie gazowym (rys. 2). W obu pojemnikach podtrzymywane jest jednakowe ciśnienie \(p,\) w jednym z nich podtrzymywana jest temperatura \(T,\) w drugim \(2T.\) Znaleźć ciśnienie i temperaturę w środkowym naczyniu w stanie równowagi.