Liczbę całkowitą dodatnią nazywamy dobrą, jeśli wśród jej dzielników znajdują się dokładnie dwie liczby pierwsze. Udowodnić, że wśród dowolnych 18 kolejnych liczb całkowitych dodatnich co najmniej jedna z liczb nie jest dobra.
Kwadratowa plansza jest podzielona na \(n^2\) prostokątnych pól za pomocą \(n-1\) prostych poziomych i \(n-1\) prostych pionowych. Pola pomalowane są w szachownicę. Wiadomo, że na jednej przekątnej wszystkie pola są czarne i kwadratowe. Udowodnić, że całkowita powierzchnia wszystkich czarnych pól jest nie mniejsza niż całkowita powierzchnia wszystkich białych pól.
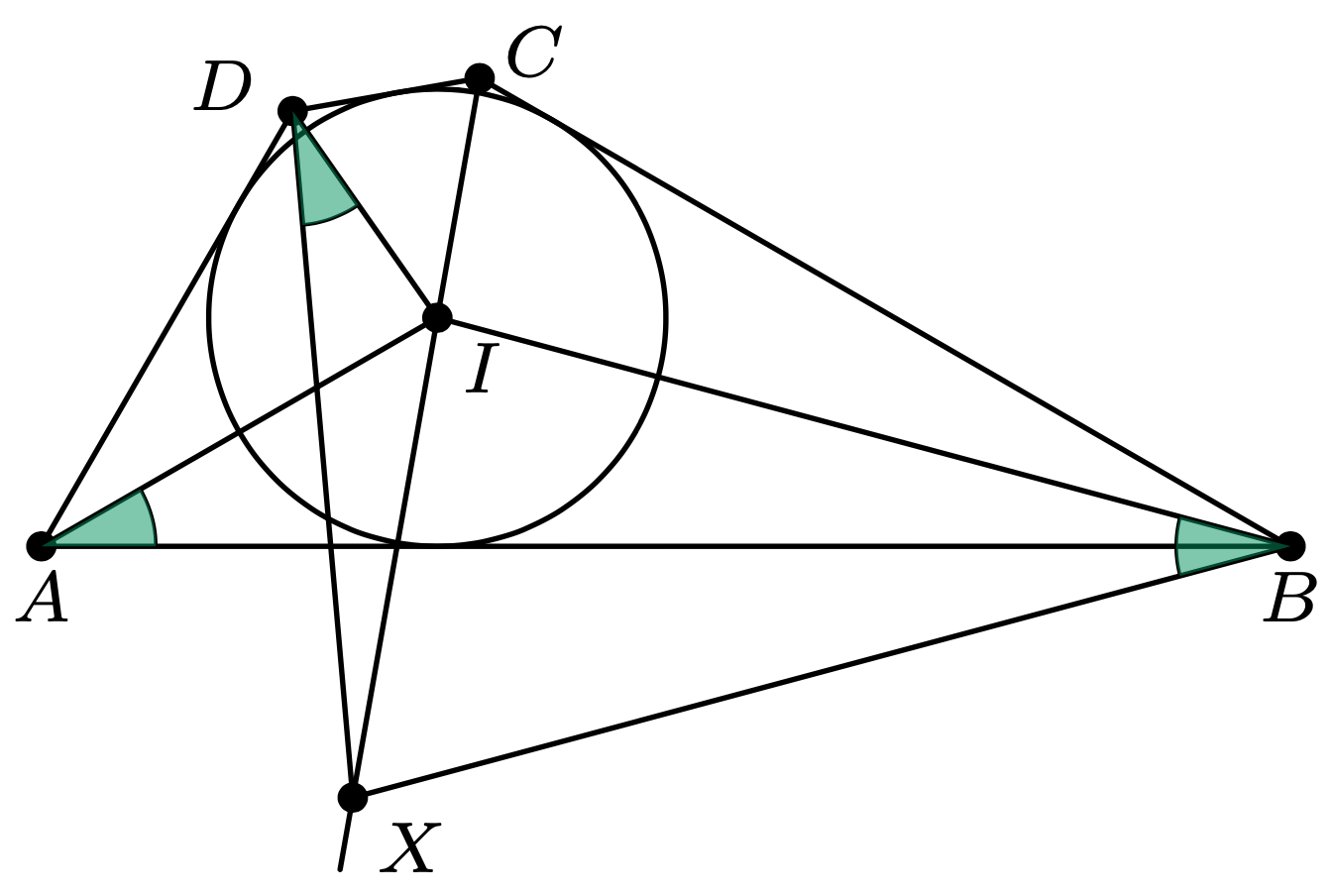
Punkt \(I{}\) jest środkiem okręgu wpisanego w czworokąt wypukły \(ABCD.\) Udowodnić, że na prostej \(CI\) istnieje punkt \(X\) taki, że \[\measuredangle XBI=\measuredangle XDI=\measuredangle BAI.\]
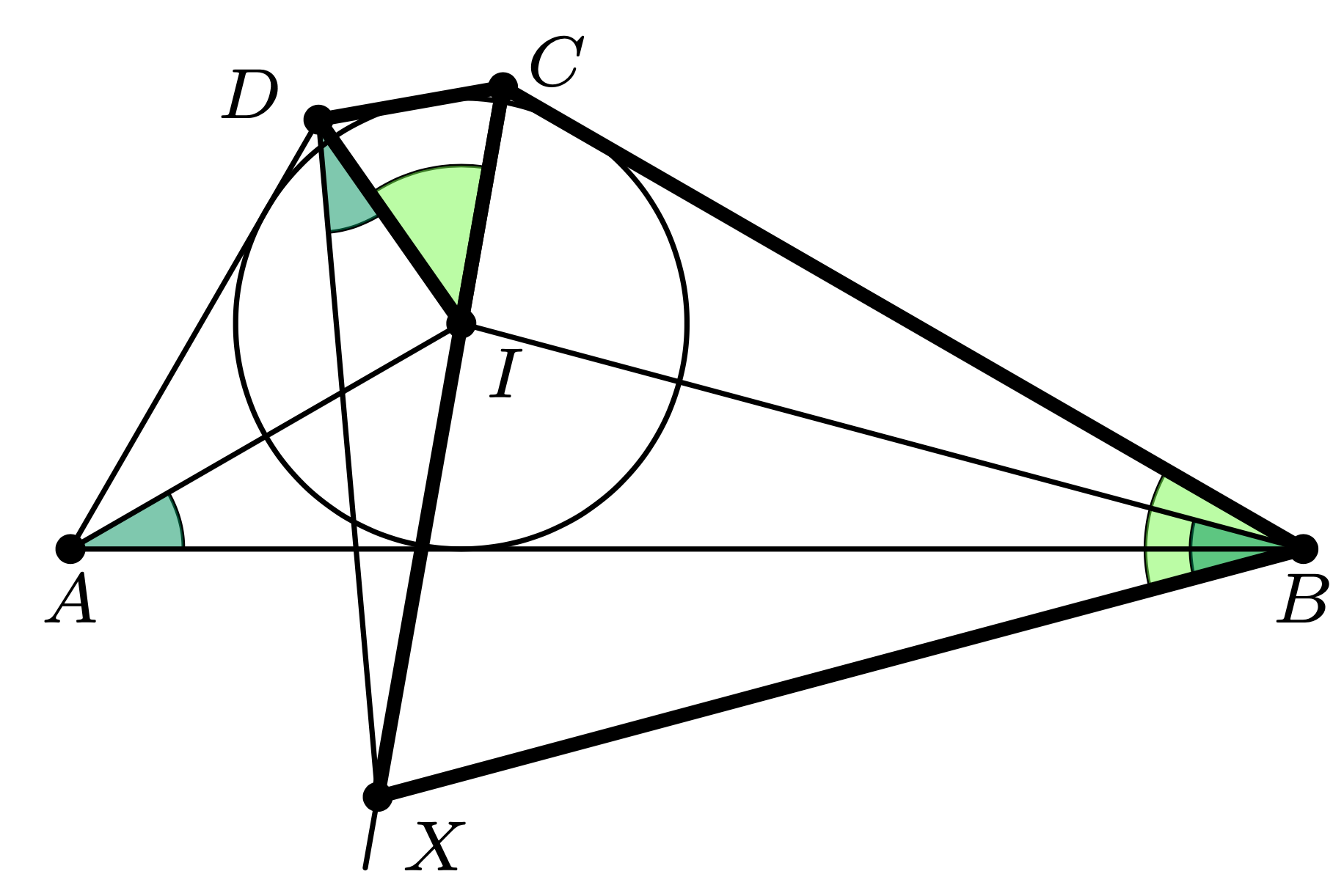 Zatem
\[\begin{aligned}
\measuredangle CBI+\measuredangle IBX&=\measuredangle CBX=\measuredangle
CID=\\&=\measuredangle 180^{\circ}-\measuredangle ICD-\measuredangle IDC=\\&=\measuredangle IBA+\measuredangle IAB,
\end{aligned}\]
gdzie w
ostatniej równości skorzystaliśmy z tego, że suma \(\measuredangle ICD+\measuredangle IDC+\measuredangle
IBA+\measuredangle IAB\) jest równa połowie sumy kątów wewnętrznych w czworokącie \(ABCD,\) czyli \(180^{\circ}.\)
Zatem
\[\begin{aligned}
\measuredangle CBI+\measuredangle IBX&=\measuredangle CBX=\measuredangle
CID=\\&=\measuredangle 180^{\circ}-\measuredangle ICD-\measuredangle IDC=\\&=\measuredangle IBA+\measuredangle IAB,
\end{aligned}\]
gdzie w
ostatniej równości skorzystaliśmy z tego, że suma \(\measuredangle ICD+\measuredangle IDC+\measuredangle
IBA+\measuredangle IAB\) jest równa połowie sumy kątów wewnętrznych w czworokącie \(ABCD,\) czyli \(180^{\circ}.\)
Ponieważ \(\measuredangle CBI=\measuredangle IBA,\) więc powyższa równość implikuje, że \(\measuredangle IBX=\measuredangle IAB.\) Analogicznie do dowodu podobieństwa trójkątów \(CID\) i \(CBX\) możemy uzasadnić podobieństwo trójkątów \(CIB\) i \(CDX,\) skąd \[\measuredangle XDI=\measuredangle CID-\measuredangle IXD = \measuredangle CBX - \measuredangle IBC=\measuredangle IBX,\] co kończy dowód.
Mgła jest zawiesiną kropelek wody w powietrzu. Oszacuj gęstość mgły \(n,\) to jest liczbę kropelek o średnicy \(d = 20\) \(\mu\)m w metrze sześciennym powietrza, jeśli skutkiem mgły jest ograniczenie widoczności do \(l = 100\) m. Jaka masa kropelek mgły (wody) zawarta jest w metrze sześciennym powietrza? Gęstość wody \(\rho = 10^3\) kg/m\(^3.\)
O wielkości kropelek decydują warunki, w jakich mgła powstaje, i dla różnych rodzajów mgły średnice kropelek mieszczą się przeważnie w przedziale od 10 \(\mu\)m do 20 \(\mu\)m, ale czasem osiągają rozmiary sięgające 40 \(\mu\)m. Ważne dla kierowców: widoczność ograniczona do 100 m wymaga zmniejszenia prędkości poniżej 80 km/h (przy 50 m poniżej 50 km/h). W niektórych krajach znaki na poboczu autostrad wskazują dopuszczalne prędkości w zależności od widoczności – liczby widzianych przez kierowcę znaczników wzdłuż brzegu pasa ruchu.
Soczewka skupiająca tworzy rzeczywisty obraz przedmiotu. Poprzeczne rozmiary obrazu są \(p\) razy większe od rozmiarów przedmiotu. Ile wynosi powiększenie podłużne obrazu? Po obu stronach soczewki znajduje się ten sam ośrodek (powietrze).
Ostatnia, przybliżona równość wynika z faktu, że \(p = y/x\) i dla \(x'\) bliskich \(x\) stosunki \(y'/x'\) i \(y/x\) są w dobrym przybliżeniu równe. Jest tak, gdy \(|x'-x| \ll f\) oraz \({|x'-x| \ll x -f}.\)