Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
W literaturze dotyczącej sieci społecznych istnieje teoria nazywana sześcioma stopniami oddalenia. Mówi ona, że dowolne dwie osoby żyjące na Ziemi są nie więcej niż sześć znajomości od siebie, tzn. dla każdej pary \(A,\) \(G\) da się wskazać ciąg pięciu pośredników \(B,C,D,E,F\) takich, że \(A\) zna się z \(B,\) \(B\) zna się z \(C,\) … i w końcu \(F\) zna się z \(G.\) Teoria ta nie została udowodniona, a w ogóle nie jest pewnie prawdziwa. Wyraża jednak słuszną ideę, że w sieci społecznej jesteśmy dużo bliżej innych, niż mogłoby nam się wydawać.
Wyobraźmy sobie jednak świat równoległy, w którym wszystko jest odwrotnie. Jeżeli w normalnym świecie kogoś znam, to w świecie równoległym go nie znam i odwrotnie. Czy możemy coś powiedzieć o odległości najdalszych osób w takim świecie? Czy jest większa niż w naszym świecie? Nie będziemy przyjmować za dużo założeń na temat sieci społecznej ludzi na Ziemi, bo – szczerze mówiąc – nie za dużo wiemy.
Używając bardziej poważnej terminologii, zastanawiamy się, jaka jest średnica (czyli właśnie odległość najdalszych wierzchołków) dopełnienia grafu przedstawiającego sieć społeczną wszystkich ludzi na Ziemi.
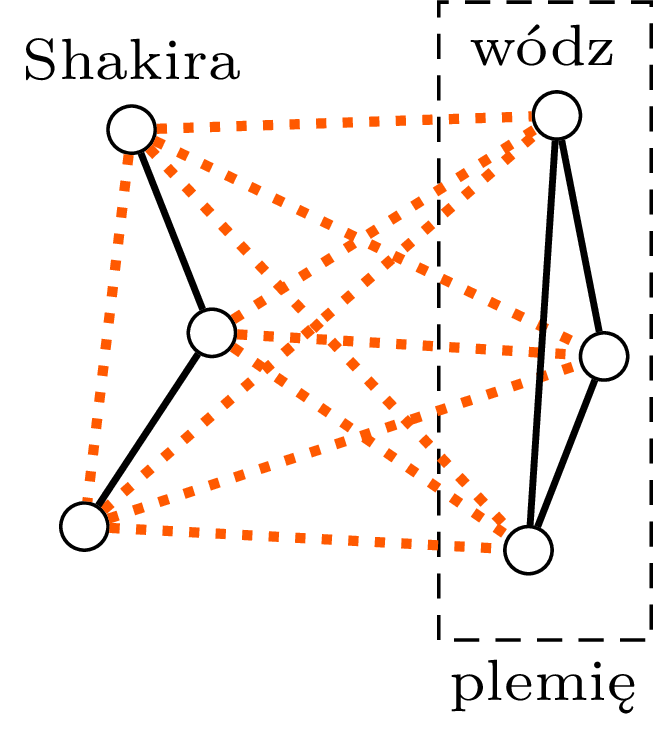
Rozważmy najpierw przypadek, w którym sieć społeczna ludzi na Ziemi jest niespójna, tzn. istnieje pewna grupa ludzi, którzy nie znają nikogo spoza tej grupy. Powiedzmy, że jest to jakieś dzikie plemię zamieszkujące jedną z wysp archipelagu Andamandów. Łatwo zauważyć, że w świecie równoległym to plemię byłoby niesamowicie popularne! Wódz plemienia regularnie występowałby w ,,Tańcu z Gwiazdami”, a wszyscy członkowie otrzymywaliby miliony życzeń urodzinowych na Facebooku. A jaka byłaby odległość najdalszych osób? Wyróżnijmy dwie osoby – wodza plemienia oraz kogoś spoza, np. Shakirę. Każda osoba z plemienia znałaby Shakirę, a każda osoba spoza plemienia znałaby wodza. Wódz plemienia znałby także Shakirę. Łatwo więc zauważyć, że każde dwie osoby w równoległym świecie znałyby się lub miały jakiegoś wspólnego znajomego: jeżeli jedna jest z plemienia, a druga spoza, to znałyby się bezpośrednio. Jeżeli obie są z plemienia, to obie znałyby Shakirę, a jeżeli obie są spoza niego, to znałyby wodza. Odległość najdalszych osób jest więc nie większa niż dwa.
Kropkowane linie oznaczają znajomości w świecie równoległym
No dobrze, załóżmy jednak przeciwnie, że sieć społeczna ludzi na Ziemi jest spójna, tzn. dla każdej pary osób możemy znaleźć ścieżkę znajomości, która je łączy. Oznacza to między innymi, że jednak wspomniane plemię kontaktuje się ze światem zewnętrznym, na przykład aby śledzić rozgrywki polskiej Ekstraklasy, i przynajmniej jedna osoba z plemienia zna przynajmniej jedną osobę spoza niego. Co teraz możemy powiedzieć o odległości najdalszych osób?
Na pewno na Ziemi są dwie osoby, które nie znają się osobiście i nie mają wspólnych znajomych (czyli są w odległości co najmniej trzy). Załóżmy, że jesteśmy to my: ja i Ty, Czytelniku.
Jeżeli nie jesteśmy to jednak my, to możemy przyjąć, że artykułu tego nie piszę ja, a mieszkaniec małej wioski we wschodnich Chinach, który przypadkowo włada językiem polskim.
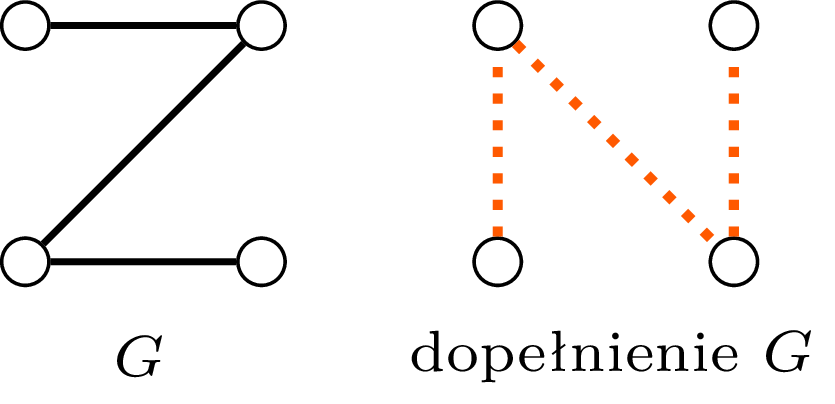
Pokazaliśmy więc, że graf lub jego dopełnienie ma średnicę nie większą niż 3. Oszacowania tego nie da się poprawić, co pokazują litery Z i N:
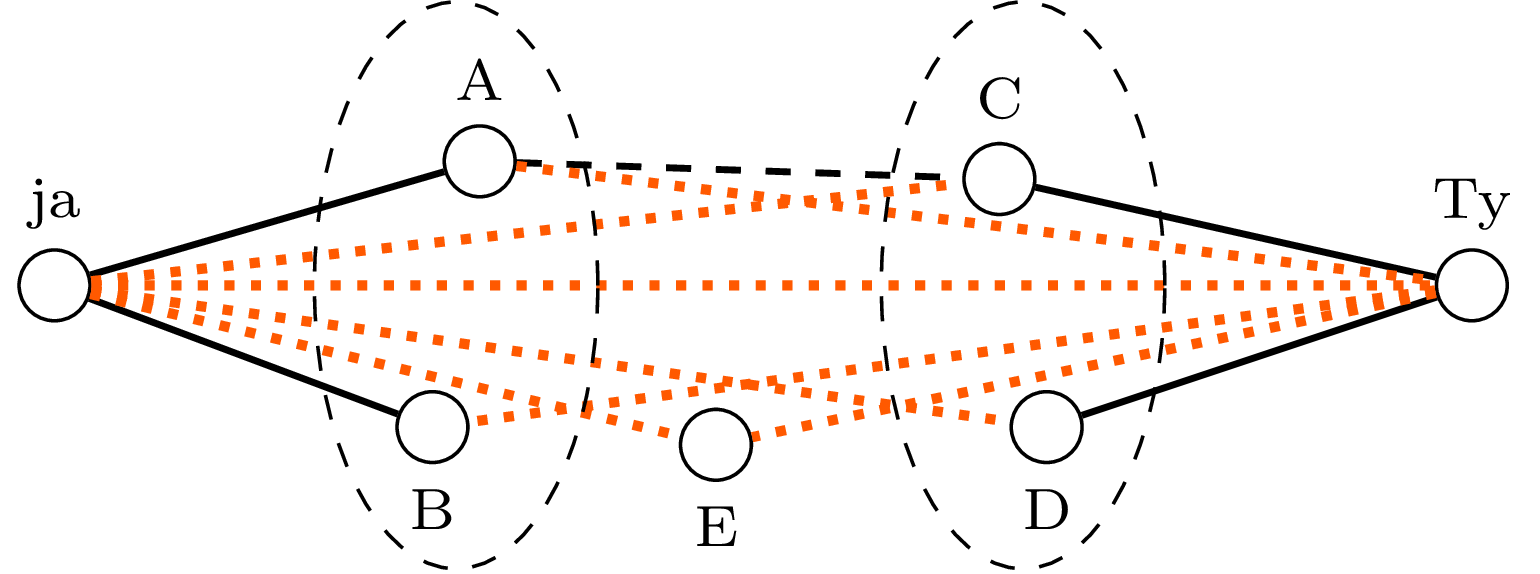
Nie mamy wspólnych znajomych, a zatem w równoległym świecie każdy musi znać mnie lub Ciebie (lub i mnie, i Ciebie). Znamy się w nim także my. Super! Weźmy dowolne dwie osoby. Jeżeli obie w równoległym świecie znają mnie, jak \(C\) i \(D\) na obrazku powyżej, to mamy ścieżkę \(C\)–ja–\(D.\) Jeżeli obie znają Ciebie, jak \(A\) i \(E,\) to mamy ścieżkę \(A\)–Ty–\(E.\) Jeżeli jedna zna mnie, a druga zna Ciebie, jak \(D\) i \(A,\) to mamy ścieżkę \(D\)–ja–Ty–\(A.\) Najdalsza odległość jest zatem nie większa niż trzy!
Wynik 3 można było też uzyskać bezpośrednio, dzieląc 6 (stopni oddalenia) na 2 (światy).
Teoria sześciu stopni jest ciężka do weryfikacji. Nam, w sposób czysto matematyczny, udało się udowodnić jednak nową teorię: teorię trzech stopni oddalenia w równoległych światach – w naszym świecie lub w świecie równoległym odległość najdalszych osób jest nie większa niż 3!