Zadania z matematyki nr 879, 880
Termin nadsyłania rozwiązań: 30 VI 2024
Redaguje Marcin E. KUCZMA
879. Funkcje \(f\) i \(g,\) o wartościach rzeczywistych, są określone na przedziale \([a,b]\); funkcja \(g\) jest rosnąca; \({f(a)>0>f(b)}.\) Wiadomo ponadto, że różnica \({f-g}\) jest funkcją ciągłą. Udowodnić, że w pewnym punkcie przedziału \((a,b)\) funkcja \(f\) przyjmuje wartość 0.
880.
Rozstrzygnąć, czy zbiór wszystkich dodatnich liczb wymiernych \({\bf Q}_{+}\) daje się przedstawić w postaci sumy dwóch zbiorów rozłącznych \(A,B\) tak, by miały miejsce następujące implikacje (dla \({x,y\in{\bf Q}_{+}}\)):
\(\bullet\) jeśli \({xy=1},\) to \({x\in{A},\;y\in{A}}\) lub \({x\in{B},\;y\in{B}}\);
\(\bullet\) jeśli \({|x-y|=1},\) to \({x\in{A},\;y\in{B}}\) lub \({x\in{B},\;y\in{A}}.\)
Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
865 (\(WT = 1{,}27\)) i 866 (\(WT = 2{,}68\))
z numeru 9/2023
Radosław Kujawa Wrocław 43,57 Paweł Najman Kraków 43,16 Marek Spychała Warszawa 41,47 Adam Woryna Ruda Śl. 40,91 Janusz Fiett Warszawa 40,89 Jerzy Cisło Wrocław 38,97 Piotr Kumor Olsztyn 37,94 Janusz Olszewski Warszawa 37,56 Paweł Kubit Kraków 36,11 Piotr Wiśniewski Warszawa 33,64
Zadanie 880 zaproponował pan Paweł Kubit z Krakowa.
Rozwiązania zadań z numeru 12/2023
Przypominamy treść zadań:
871. Dana jest liczba całkowita parzysta \({n>0}.\) (a) Dowieść, że w przedziale \([n{+}1,2n{+}1]\) zawiera się \(n\)-elementowy zbiór liczb całkowitych \(M\) taki, że żaden jego element nie jest dzielnikiem sumy wszystkich liczb zbioru \(M.\) (b) Wyjaśnić, czy zawsze istnieją (w tym przedziale) co najmniej dwa różne zbiory \(n\)-elementowe o powyższych własnościach.
Niech \({M^*=\{n{+}1,n{+}2,\ldots,2n{+}1\}}\) i niech \(S\) będzie sumą elementów zbioru \(M^*.\) Niech \({M_k=M^*\setminus\{k\}}\) (dla \({k\in{M^*}}\)). Będziemy mówili, że liczba \({k\in{M^*}}\) jest ciekawa, gdy suma elementów zbioru \(M_k\) (czyli liczba \({S-k}\)) nie dzieli się przez żaden z nich.
(a) Należy wykazać, że co najmniej jedna liczba \({k\in{M^*}}\) jest ciekawa. Przyjmijmy dalsze oznaczenie:
\[N_k=\{i\in{M^*}\colon\;i\,|\,S-k\}.\]
Odnotujmy proste własności:
\(W1.\) Jeśli \({N_k=\emptyset},\) to liczba \(k\) jest ciekawa.
\(W2.\) Jeśli \({k|S},\) to \({k\in{N_k}}\) (więc \({N_k\ne\emptyset}\)).
\(W3.\) Jeśli \({k|S}\) oraz \({|N_k|=1},\) to liczba \(k\) jest ciekawa.
\(W4.\) Zbiory \(N_k\) są parami rozłączne.
Własności \(W1,\) \(W2,\) \(W3\) są oczywiste. Dowód \(W4\): gdyby \({i_0\in{N_k}\cap{N_l}}\) (\({k>l}\)), to \({i_0|k-l}\); a to niemożliwe, bo \({i_0\ge{n+1}},\) zaś \({k-l\le(2n{+}1)-(n{+}1)=n}.\) Z własności \(W4\) wynika, że
\[\sum_{k\in{M^*}}|N_k|\le\bigl|M^*\bigr|=n+1.
\ \ \ (*)\]
Suma \((*)\) ma \({n+1}\) składników. Jeżeli któryś z nich jest zerem, to jest to już teza (a) (własność \(W1\)). Jeżeli nie, to wszystkie są równe 1. Prosty rachunek pokazuje, że \({S=cd},\) gdzie \({c=n+1},\) \({d={3\over 2}n+1}\) (\({c,d\in{M^*}}\)); więc i teraz dostajemy tezę (a), bo (dzięki \(W3\)) liczba \(c\) jest ciekawa (\(d\) zresztą też).
(b) Tu też odpowiedź jest twierdząca: wykażemy, że w zbiorze \(M^*\) są co najmniej dwie liczby ciekawe. Jeśli wśród składników sumy \((*)\) są co najmniej dwa zera, to gotowe (\(W1\)). Jeśli wszystkie są dodatnie, to są jedynkami i znów (wobec \(W3\)) liczby \(c\) i \(d\) są obie ciekawe.
Pozostaje przypadek, gdy wśród składników sumy \((*)\) jest dokładnie jedno zero; niech np. \({|N_e|=0}\): liczba \(e\) jest więc ciekawa (\(W1\)); \({e\ne{c,d}},\) bo \({N_c,N_d\ne\emptyset}\) (\(W2\)). Pozostałe składniki sumy \((*)\) to albo same jedynki, albo dwójka i poza nią jedynki. Co najmniej jedna z liczb \(c,d\) musi być wśród jedynek – jest więc ciekawa (\(W3\)); dowód zakończony.
872. Wielomiany \(W_1,\ldots,W_m\) (jednej zmiennej), stopni dodatnich, mają dodatnie współczynniki całkowite. Wykazać, że dla nieskończenie wielu liczb całkowitych \({n>0}\) wartości \(W_1(n),\ldots,W_m(n)\) są jednocześnie liczbami złożonymi.
Oznaczmy \({W_j(1)=c_j}.\) Weźmy dowolną liczbę \(n\) postaci \({n=kc_1\ldots{c_m}+1}\) (\({k\in{\bf N}}\)). Ustalmy \({j\in\{1,\ldots,m\}}.\) Różnica \({W_j(n)-W_j(1)}\) dzieli się przez \({n-1},\) więc i przez \(c_j.\) Skoro \({c_j=W_j(1)},\) znaczy to, że \(W_j(n)\) dzieli się przez \(c_j.\) Przy tym dla dostatecznie dużych \(n\) wartość \(W_j(n)\) przekracza \(c_j\); jest więc liczbą złożoną. Tak jest dla każdego numeru \(j,\) skąd wniosek, że dla dostatecznie dużych \(n\) (rozważanej postaci) wszystkie wartości \(W_1(n),\ldots,W_m(n)\) są liczbami złożonymi.
Zadania z fizyki nr 776, 777
Termin nadsyłania rozwiązań: 30 VI 2024
Redaguje Elżbieta ZAWISTOWSKA
776. Na poziomej powierzchni stoi jednorodna, cienka obręcz o masie \(M\) i promieniu \(R.\) Poziomą średnicę obręczy stanowi lekka, gładka rurka, wewnątrz której umieszczono kulkę o masie \(m\) przylegającą do rurki i połączoną z obręczą dwiema sprężynami o współczynnikach sprężystości \(k\) (rys. 1). Przytrzymując obręcz, kulkę odchylono w lewo o \(x,\) po czym układ pozostawiono samemu sobie. Znaleźć przyspieszenie środka obręczy w chwili początkowej, zakładając brak poślizgu obręczy.
Rys. 1
777. Trzy jednakowe kondensatory o pojemnościach \(C\) połączono szeregowo, podłączono do źródła o sile elektromotorycznej \(\mathcal E\) i po naładowaniu odłączono od baterii. Następnie do układu podłączono jednocześnie dwa oporniki o oporach \(R\) (rys. 2). Jaka ilość ciepła wydzieli się na każdym oporniku? Jakie natężenia mają prądy płynące przez oporniki w chwili, gdy napięcie na środkowym kondensatorze jest 10 razy mniejsze od siły elektromotorycznej baterii?
Rys. 2
Rozwiązania zadań z numeru 12/2023
Przypominamy treść zadań:
768. Otwarta z dwóch stron rurka w kształcie litery U porusza się z prędkością \(v\) równolegle do powierzchni cieczy (rys. 3). Przekrój zanurzonej w cieczy dolnej części rurki wynosi \(S_1,\) a górnej, znajdującej się nad cieczą, jest równy \(S_2.\) Jaka siła zewnętrzna działa na rurkę w kierunku poziomym? Tarcie i powstawanie fal należy zaniedbać. Gęstość cieczy wynosi \(\rho.\)
Rys. 3
W inercjalnym układzie odniesienia związanym z rurką, ciecz w dolnej części rurki porusza się z prędkością \(v.\) W czasie \(\Delta t\) do rurki wpływa porcja cieczy o masie \(m=\rho S_1v\Delta t\) i pędzie \(p_1=mv=\rho S_1v^2\Delta t.\) W tym samym czasie porcja o takiej samej masie wycieka z górnej części rurki z prędkością \(u={vS_1}/{S_2},\) a jej pęd \(p_2=\rho S_2u^2\Delta t=\rho v^2{S_1}^2{\Delta t}/{S_2}.\) Wektor zmiany pędu cieczy w rurce w czasie \(\Delta t\) ma wartość \(\Delta p=mv-\left(-mu\right)=\rho S_1\left(1+{S_1}/{S_2}\right)v^2\Delta t\) i skierowany jest w prawo. Ciecz działa na rurkę w lewo, a szukana siła zewnętrzna działająca na rurkę nie zależy od wyboru inercjalnego układu odniesienia, skierowana jest w prawo i ma wartość \[F={\Delta p}/{\Delta t}=\rho S_1\left(1+{S_1}/{S_2}\right)v^2.\]
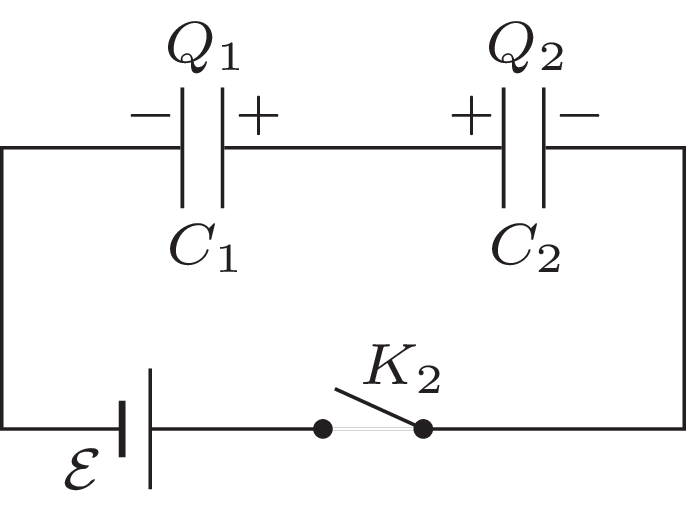
769. W układzie przedstawionym na rysunku 4 na początku wszystkie klucze są otwarte, a kondensatory o pojemnościach \(C_1\) i \(C_2\) nienaładowane. Klucze \(K_1\) i \(K_3\) zostały zamknięte i po ustaleniu równowagi otwarte, po czym zamknięty został klucz \(K_2.\) Znaleźć napięcie końcowe na kondensatorze \(C_1.\) Siła elektromotoryczna baterii wynosi \(\mathcal E.\)
Rys. 4
Po zamknięciu kluczy \(K_1\) i \(K_3\) kondensatory są połączone równolegle z baterią, a ładunki na nich to \({Q_1=C}_1\varepsilon\) i \(Q_2=C_2\varepsilon .\) Sytuację przed zamknięciem klucza \(K_2\) przedstawia rysunek 5.
Po zamknięciu klucza \(K_2\) do prawej okładki kondensatora \(C_2\) dopływa ładunek \(q,\) z lewej okładki kondensatora \(C_1\) odpływa taki sam ładunek. Całkowity ładunek na wewnętrznych okładkach pozostaje niezmieniony (rys. 6). Z drugiego prawa Kirchhoffa mamy:
\(\varepsilon ={{\left(Q_2-q\right)}/{C_2}-{\left(Q_1+q\right)}/{C}}_1,\) stąd \(q={C_1C_2\varepsilon }/{\left(C_1+C_2\right)}.\)
Napięcie końcowe na kondensatorze \(C_1\) wynosi:
\[U={\left(Q_1+q\right)}/{C_1}={\varepsilon \left(C_1+2C_2\right)}/{\left(C_1+C_2\right)}.\]
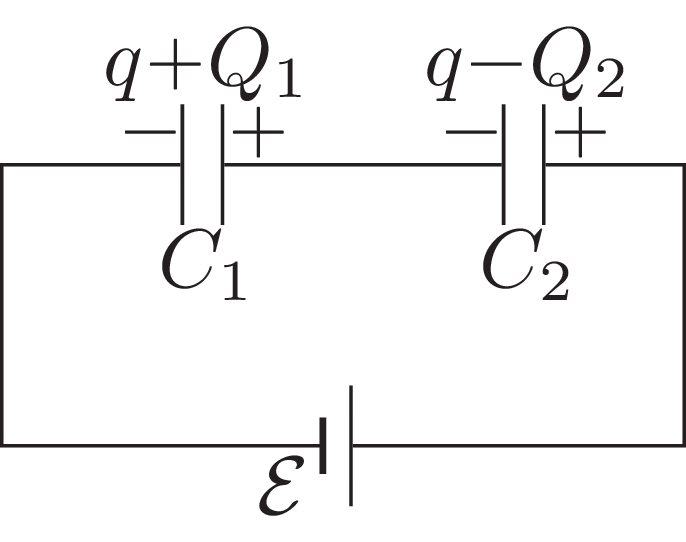
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
762 (\(WT=3{,}01\)), 763 (\(WT=2{,}46\)) z numeru 9/2023
Tomasz Rudny Poznań 43,41 Marian Łupieżowiec Gliwice 2–43,02 Tomasz Wietecha Tarnów 16–40,60 Jacek Konieczny Poznań 38,28 Konrad Kapcia Poznań 2–35,60 Ryszard Woźniak Kraków 32,96 Ryszard Baniewicz Włocławek 1–32,41 Paweł Perkowski Ożarów Maz. 5–24,61 Andrzej Nowogrodzki Chocianów 3–22,20 Paweł Kubit Kraków 15,73 Jan Zambrzycki Białystok 4–13,69 W rozwiązaniu zadania 762 w numerze styczniowym prawa strona równania wyrażającego zasadę zachowania energii powinna mieć postać: \(3\sqrt{p_{f}^{2}c^{2}/9+m^{2}c^{4}}.\)