Zadania z matematyki nr 877, 878
Termin nadsyłania rozwiązań: 31 V 2024
Redaguje Marcin E. KUCZMA
877. Wyjaśnić, czy istnieje na płaszczyźnie konfiguracja pięciu różnych punktów \(A,B,C,P,Q,\) w której zachodzą równości \[PA=AB=BQ,\ \ \ PB=BC=CQ,\ \ \ PC=CA=AQ,\] a punkty \(A,B,C\) są wierzchołkami trójkąta (a) ostrokątnego, (b) rozwartokątnego.
878. Znaleźć liczbę naturalną \({r>2},\) dla której istnieje nieskończenie wiele \(r\)-elementowych zbiorów różnych liczb pierwszych \(\{p_1,\ldots,p_r\}\) takich, że każda z liczb \({2^{p_i-1}-1}\) (\({i=1,\ldots,r}\)) jest podzielna przez iloczyn \(p_1\dots{p_r}.\) Im większa liczba \(r,\) tym cenniejsze rozwiązanie.
Zadanie 878 zaproponował pan Piotr Kumor z Olsztyna w nawiązaniu do zadania 678 (naszej ligi: \(\Delta^7_{14}\); omówienie: \(\Delta^2_{15}\)), a także do zadania 8 z obozu OM (Zwardoń 2010) <om.sem.edu.pl>, zakładka Obóz naukowy.
Rozwiązania zadań z numeru 11/2023
Przypominamy treść zadań:
869. Funkcja \(g\) przyporządkowuje każdej (uporządkowanej) parze \(x,y\) liczb rzeczywistych dodatnich wartość \(g(x,y),\) określoną jako najmniejsza liczba z trójki \(x,\) \({1/{y}},\) \({(xy+1)/{x}}.\) Wyznaczyć kres górny wartości \(g(x,y),\) gdy \(x\) oraz \(y\) przebiegają zbiór wszystkich liczb dodatnich.
Wartości funkcji \(g\) są dodatnie. Niech \(s\) będzie dowolną jej wartością. Istnieją więc liczby \({x,y>0},\) dla których \({s=g(x,y)}.\) Zgodnie z określeniem funkcji \(g\) spełnione są jednocześnie nierówności \[x\ge{s},\ \ \ \ \frac1y\ge{s},\ \ \ \ \frac{xy+1}x\ge{s}\] (jedna z nich staje się równością). Wynika z nich, że \[\frac1x\le\frac1s\,,\ \ \ y\le\frac1s\,,\ \ \ s\le\frac{xy+1}x=y+\frac1x\le\frac2s\,.\] Ostatnia nierówność pokazuje, że \({s^2\le2},\) czyli \({s\le\sqrt2}.\) Tak więc wartości funkcji \(g\) nie przekraczają \(\sqrt2.\) Przy tym \[g\Bigl(\sqrt2\,,\frac1{\sqrt2}\,\Bigr)=\min\Bigl\{\sqrt2, \sqrt2, \frac{1+1}{\sqrt2}\,\Bigr\}=\sqrt2.\] Zatem liczba \(\sqrt2\) jest szukanym kresem górnym wartości funkcji \(g.\)
870.
(a)
Wykazać, że z odcinków łączących dowolny punkt płaszczyzny z wierzchołkami trójkąta równobocznego (leżącego w tej płaszczyźnie) można zbudować pewien trójkąt (być może zdegenerowany).
(b)
Trójkąt równoboczny jest zanurzony w przestrzeni (trójwymiarowej). Wyjaśnić, czy – analogicznie – zawsze można z odcinków łączących dowolny punkt przestrzeni z wierzchołkami tego trójkąta zbudować pewien trójkąt (być może zdegenerowany).
(a) Niech \(P\) będzie dowolnym punktem w płaszczyźnie trójkąta równobocznego \(ABC.\) Rozważmy obrót płaszczyzny wokół punktu \(C\) o kąt \(60^\circ,\) przenoszący punkt \(A\) do pozycji punktu \(B.\)
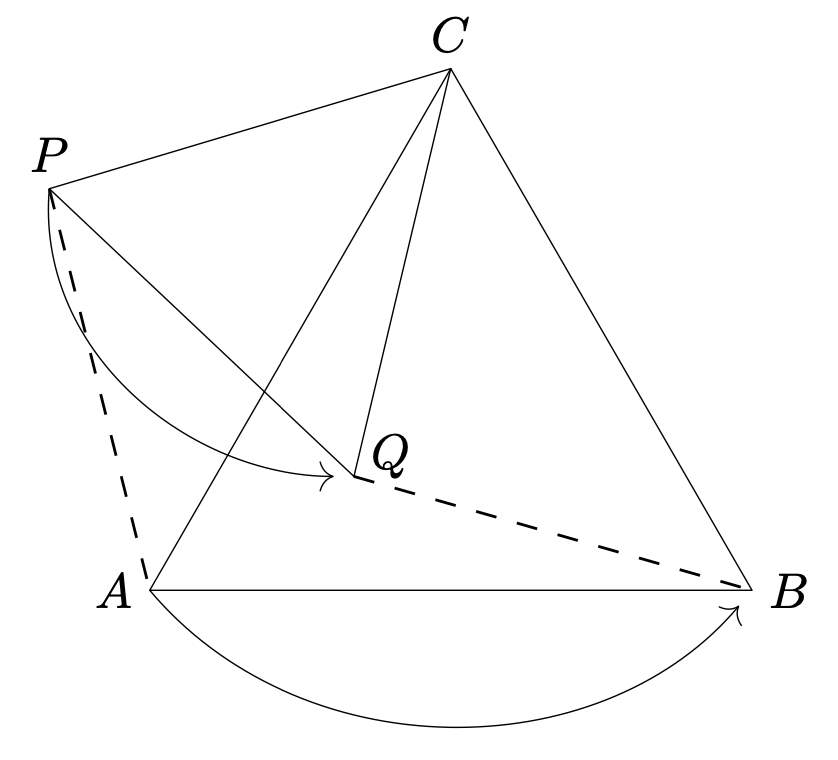
Obraz punktu \(P\) nazwijmy \(Q.\) Odcinki \(CP\) i \(CQ\) są równej długości i tworzą kąt \(60^\circ,\) więc trójkąt \(CPQ\) jest równoboczny. Odcinek \(AP\) przechodzi na odcinek \(BQ.\) Trójkąt \(BPQ\) (być może zdegenerowany do odcinka) ma boki długości \({BQ=AP},\) \(BP,\) \({PQ=CP}\); jest więc trójkątem, którego istnienie należało uzasadnić.
(b) Niech teraz \(P\) będzie dowolnym punktem w przestrzeni, leżącym poza płaszczyzną trójkąta równobocznego \(ABC.\) Wykażemy, że i teraz istnieje trójkąt o bokach długości \(AP,\) \(BP,\) \(CP.\) Przyjmijmy (b.s.o.), że najdłuższy z tej trójki jest odcinek \(CP.\) Wystarczy dowieść, że wówczas \({CP\le{AP+BP}}.\)
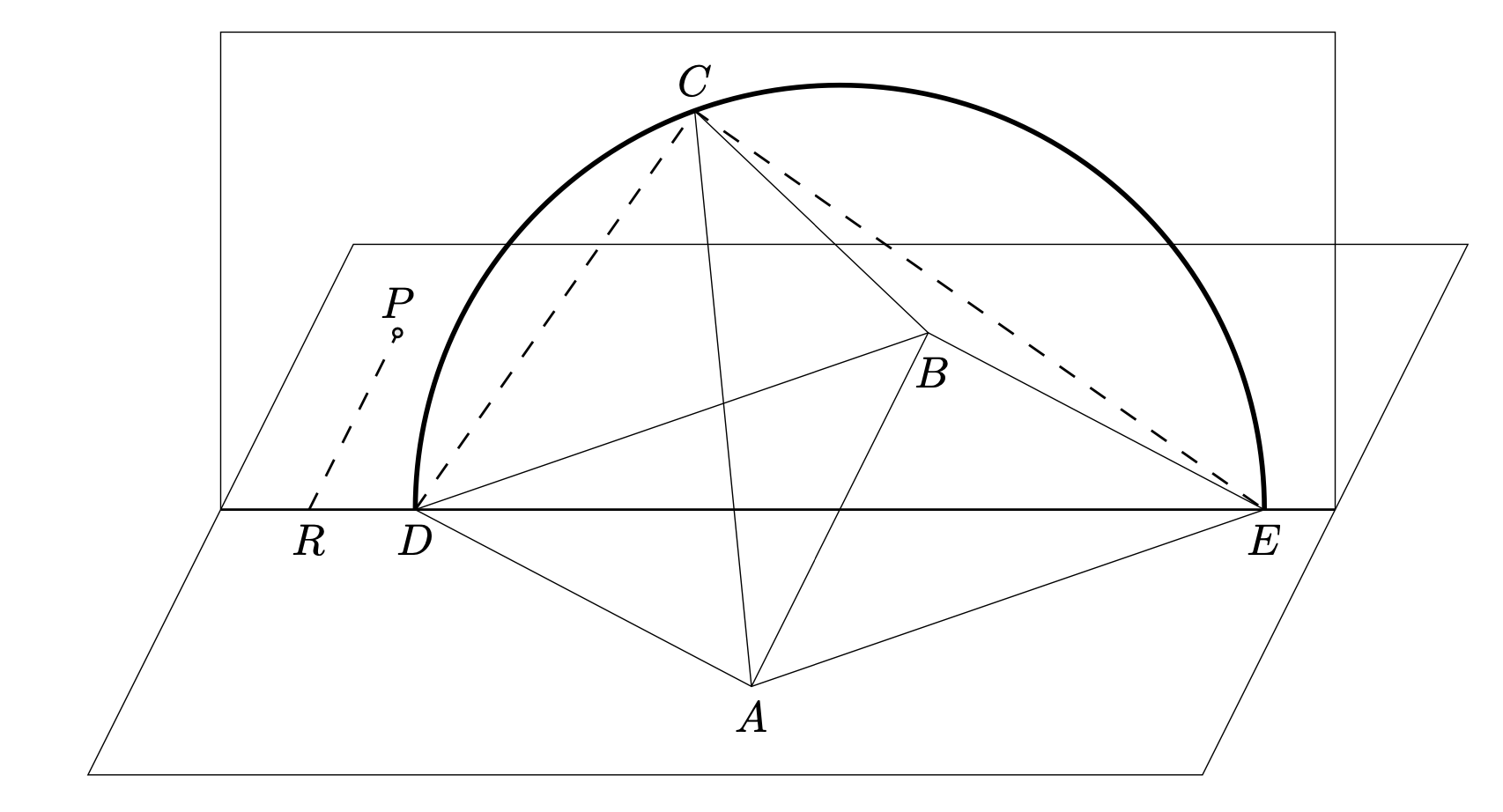
W płaszczyźnie \(ABP\) budujemy trójkąty równoboczne \(ABD\) i \(ABE\); dobieramy oznaczenia tak, by \({PD\le{PE}}.\) Wierzchołki \(C,D,E\) trójkątów foremnych o wspólnym boku \(AB\) leżą na płaszczyźnie symetralnej odcinka \(AB,\) na okręgu o średnicy \(DE\); trójkąt \(CDE\) jest prostokątny. Niech \(R\) będzie rzutem punktu \(P\) na prostą \(DE.\) Płaszczyzny \(CDE\) i \(PDE\) są prostopadłe, więc \({CR\perp{PR}}.\) Stąd \({DR=\sqrt{PD^2-PR^2}\le\sqrt{PE^2-PR^2}=ER}.\) To znaczy, że (w płaszczyźnie \(CDE\)) punkty \(C\) i \(R\) leżą po jednej stronie prostej symetralnej odcinka \(CE\) (która połowi przeciwprostokątną \(DE\)); czyli \({CR\le{ER}}.\) Stąd \({CP=\sqrt{CR^2+PR^2}\le\sqrt{ER^2+PR^2}=EP}.\)
Z części (a), zastosowanej do trójkąta \(ABE\) i punktu \(P\) (leżącego w jego płaszczyźnie) wiadomo, że z odcinków \(AP,\) \(BP,\) \(EP\) można zbudować trójkąt. Zatem \({EP\le{AP+BP}},\) więc tym bardziej \({CP\le{AP+BP}}.\)
[Istnieją różne rachunkowe metody rozwiązania zadania, tak w części (a), jak i (b).]
Zadania z fizyki nr 774, 775
Termin nadsyłania rozwiązań: 31 V 2024
Redaguje Elżbieta ZAWISTOWSKA
774. Długi klocek o podstawie kwadratowej pływa w wodzie tak, że jedna z jego powierzchni bocznych znajduje się nad powierzchnią wody i jest do niej równoległa, a klocek znajduje się w stanie równowagi trwałej. Dla jakiej gęstości materiału, z którego wykonano klocek, jest to możliwe?
775. Cienki pierścień gumowy rozkręcono wokół osi symetrii prostopadłej do płaszczyzny pierścienia. Prędkość liniowa jego elementów wynosi \(v.\) Z jaką prędkością będą rozprzestrzeniać się w tym pierścieniu monochromatyczne fale poprzeczne o małej amplitudzie?
Rozwiązania zadań z numeru 11/2023
Przypominamy treść zadań:
766. Znaleźć siłę oddziaływania dwóch połówek nieprzewodzącej kuli o promieniu \(R,\) naładowanych ze stałą gęstością objętościową, odpowiednio, \(\rho_{1}\) i \(\rho_{2}.\) Przyjąć, że kula wykonana jest z materiału o stałej dielektrycznej równej jeden.
W każdym punkcie półkuli o gęstości \({\rho }_1\) działa siła od drugiej półkuli \(d\vec{f}={\rho }_1\vec{E}dV,\) gdzie \(\vec{E}\) jest natężeniem pola elektrycznego w danym punkcie od drugiej półkuli, a \({\rho }_1dV\) to ładunek elementarnej objętości wokół punktu. Zatem siła działająca na pierwszą półkulę jest proporcjonalna do \({\rho }_1.\) Analogicznie siła działająca na drugą półkulę ze strony pierwszej jest proporcjonalna do \({\rho }_2.\) Stąd wniosek, że siła oddziaływania między półkulami \[F\sim {\rho }_1{\rho }_2={{\rho }_1}^2{{\rho }_2}/{{\rho }_1}.\] Na pierwszą półkulę działa również jej własne pole, którego wypadkowe działanie wynosi zero. Obliczymy więc siłę oddziaływania \(F_1\) z drugą półkulą o takiej samej gęstości, rozważając pole od całej kuli, a następnie wynik pomnożymy przez czynnik \({{\rho }_2}/{{\rho }_1}.\)
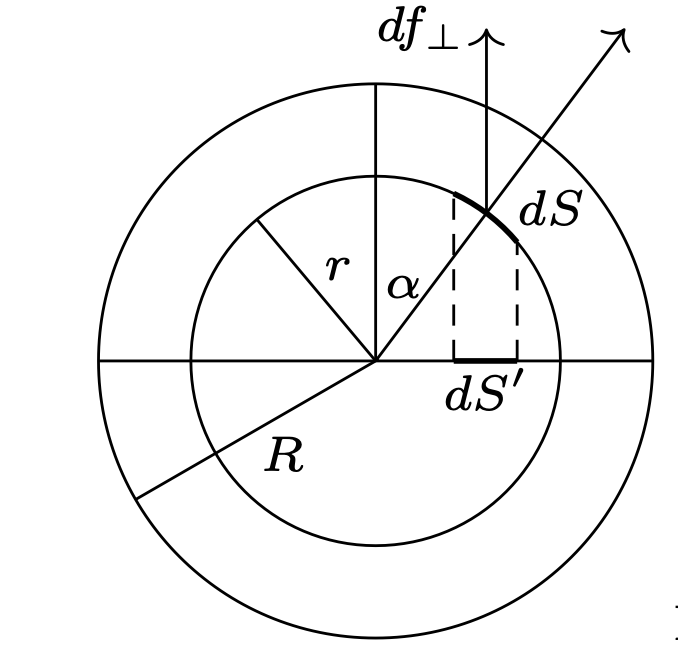Rys. 2
Zgodnie z prawem Gaussa natężenie pola wewnątrz kuli naładowanej ze stałą gęstością objętościową \({\rho }_1>0\) w odległości \(r\) od środka kuli ma wartość \({E={{\rho }_1r}/{3{\varepsilon }_{0 }}}\) i jest skierowane wzdłuż promienia. Podzielmy górną półkulę na rysunku 2 na półsferyczne warstwy. Prostopadła do powierzchni rozdziału półkul składowa siły działającej na mały element warstwy o promieniu \(r\) i powierzchni \(dS\) wynosi: \[df_{\bot }=E{\rho }_1dSdr\cos\alpha =E{\rho }_1dS'dr,\] gdzie \(dr\) jest grubością warstwy, a \(dS'=dS\cos\alpha\) rzutem powierzchni \(dS\) na powierzchnię rozdziału. Wypadkowa siła działająca na półsferę o promieniu \(r\) \[dF_1=\pi r^2df_{\bot }=\pi {{\rho }_1}^2r^3{dr}/{3{\varepsilon }_0}.\] Siła oddziaływania półkul o jednakowych gęstościach dana jest wzorem \[F_1=\textstyle\int\limits^R_0{dF_1}=\frac{\pi {{\rho }_1}^2R^4}{12{\varepsilon }_0},\] a szukana siła oddziaływania półkul o gęstościach \({\rho }_1\) i \({\rho }_2\) \[F={\pi R^4{\rho }_1{\rho }_2}/{12{\varepsilon }_0}.\]
767. Pierścienie \(O\) i \(O'\) nasunięte są na pionowe, nieruchome pręty \(AB\) i \(A'B'.\) Nierozciągliwa nić umocowana w punkcie \(A'\) przewleczona jest przez pierścień \(O'\) i przyczepiona do pierścienia \(O\) (rys. 1). Pierścień \(O'\) porusza się w dół ze stałą prędkością \(v.\) Jaka jest prędkość pierścienia \(O\) w chwili, gdy kąt \(AOO'\) ma wartość \(\alpha.\)
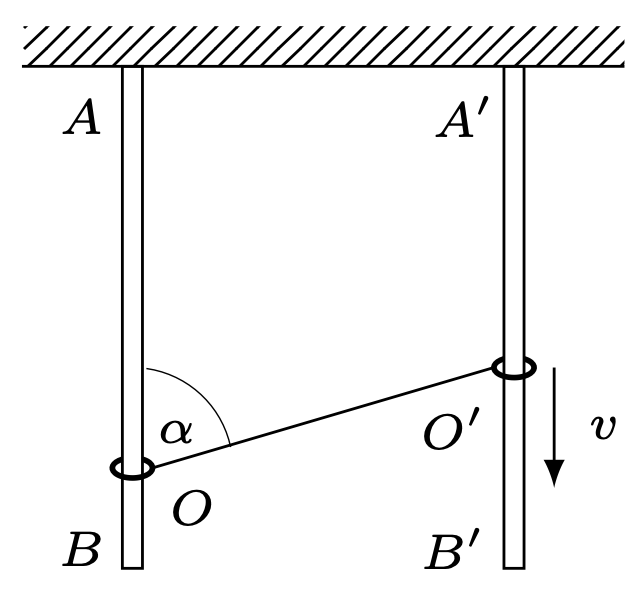Rys. 1
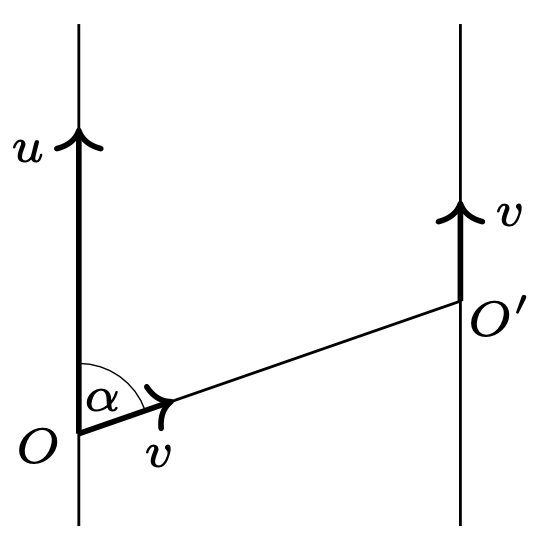Rys. 3
Ponieważ nić jest nierozciągliwa, składowa prędkości pierścienia \(O\) wzdłuż nici ma również prędkość \(v,\) a wypadkowa prędkość pierścienia w badanej chwili i w wybranym układzie wynosi: \[u={v}/{\cos\alpha .}\] W nieruchomym układzie odniesienia szukana prędkość pierścienia jest równa: \[v_O=u-v=v\left({1}/{\cos\alpha }-1\right).\]