Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
W artykule Problem bankructwa z Talmudu \(\Delta^{10}_{21}\) opisaliśmy pewną tajemnicę, która tkwiła w Talmudzie Babilońskim przez setki lat. Historia była następująca. Mężczyzna, umierając, zostawił trzy żony, którym obiecał odpowiednio 100, 200 i 300 srebrnych monet. Jego majątek nie był jednak tak duży, aby spłacić te zobowiązania. Jak powinno się podzielić pozostawiony majątek między żony? Talmud rozstrzyga tę kwestię w konkretnych przypadkach: jeżeli majątek to 100 monet, to powinno się go podzielić po równo. Jeżeli 200 monet, to pierwsza żona powinna dostać 50 monet, a pozostałe po 75. Z kolei jeżeli majątek stanowi 300 monet, to powinno się go podzielić proporcjonalnie: każda żona dostanie wówczas połowę obiecanej kwoty. Skąd biorą się jednak te sposoby podziału?
Rozwiązanie tej zagadki znaleźli dopiero w 1985 roku Robert Aumann i Michael Maschler. Nie tylko przedstawili oni metodę podziału, która pasuje do wszystkich trzech scenariuszy, ale też podali kilka jej uzasadnień. O tej metodzie i uzasadnieniach pisaliśmy w poprzednim artykule, jednak nie powiedzieliśmy, skąd ta metoda w ogóle się wzięła. Autorzy sami przyznają, że metodę tę znaleźli, używając gier koalicyjnych. O tym, jak można to zrobić, opowiemy w tym artykule.
Dokładniej pojawienie się tej metody uzasadnialiśmy tak:
,,Udowodniliśmy więc, że jest najwyżej jedno rozwiązanie problemu bankructwa spójne z rozwiązaniem sporu o ubiór. Jak ono wygląda? O tak:”
Problem bankructwa matematycznie definiuje się jako ciąg nieujemnych liczb dodatnich \((E; c_1, \dots, c_n),\) gdzie \(E\) to majątek, a \(c_1 \le \dots \le c_n\) to roszczenia \(n\) osób, które (zgodnie z historią powyżej) będziemy nazywać żonami, przy czym majątek \(E\) nie przekracza sumy roszczeń \(C = \sum_{i=1}^n c_i.\)
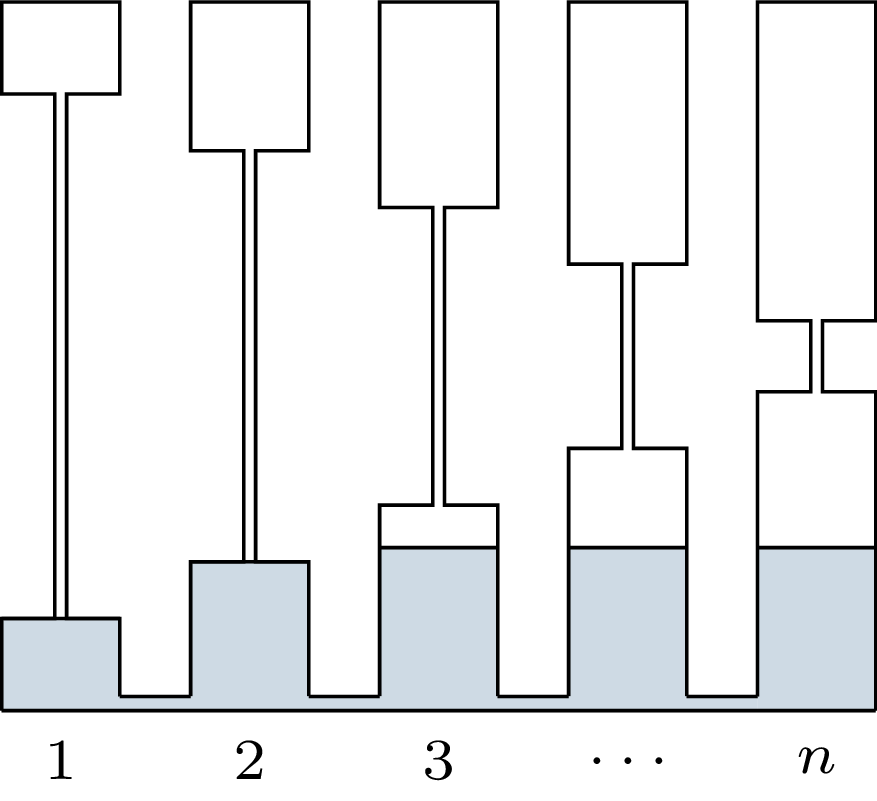
Metodę podziału znalezioną przez Aumanna i Maschlera obrazowo opisać można systemem naczyń połączonych znajdującym się na rysunku obok. Jest w nim \(n\) naczyń o pojemności \(c_1, \dots, c_n,\) każde złożone z dwóch połów połączonych bardzo cienką rurką o pomijalnej objętości. U podstawy wszystkie naczynia łączy równie cienka rurka. Do tego systemu wlewamy \(E\) wody i każdej żonie przyznajemy tyle majątku, ile wody znajdzie się w jej naczyniu.
Z układu widzimy, że jeżeli majątek jest mniejszy niż połowa sumy roszczeń, czyli \(E \le C/2,\) to pierwszych \(k\) żon (dla pewnego \(k\)) dostanie połowę swojego roszczenia. Pozostałe żony podzielą się resztą po równo, przy czym \(k\) wyznaczamy tak, aby nie dostały mniej niż \(k\)-ta żona. Jeżeli \(E > C/2,\) to możemy myśleć o dzieleniu nie majątku, a jego brakującej części – pierwszym \(k\) żonom będzie brakowało po połowie ich roszczeń, a pozostałe tak podzielą się resztą, aby brakowało im po tyle samo.
Liczbę \(k\) wyznaczamy jako największe \(j \in \{0,\dots,n\},\) dla którego zachodzi \(\sum_{i=1}^{j} c_i/2 + (n\!-\!j) c_j/2\) \(\le \min \{E,C\!-\!E\}.\)
Łatwo sprawdzić, że metoda ta zgadza się z wariantami problemu bankructwa opisanymi w Talmudzie.
Mało żon, mały kłopot
Zastanówmy się, gdzie możemy znaleźć tę rzekomą grę koalicyjną? Przypomnijmy, że gra koalicyjna to para \((N,f),\) gdzie \(N\) jest zbiorem graczy, a \(f: 2^N \rightarrow \mathbb{R}\) funkcją, która każdej grupie graczy, nazywanej koalicją, przypisuje pewną wartość (zakładamy \(f(\emptyset) = 0\)).
Od pewnego czasu gry koalicyjne pojawiają się w Delcie regularnie raz do roku: pojawiły się w numerach \(\Delta^{11}_{20}\), \(\Delta^{10}_{21}\), \(\Delta^4_{22}\) i \(\Delta^2_{23}\).
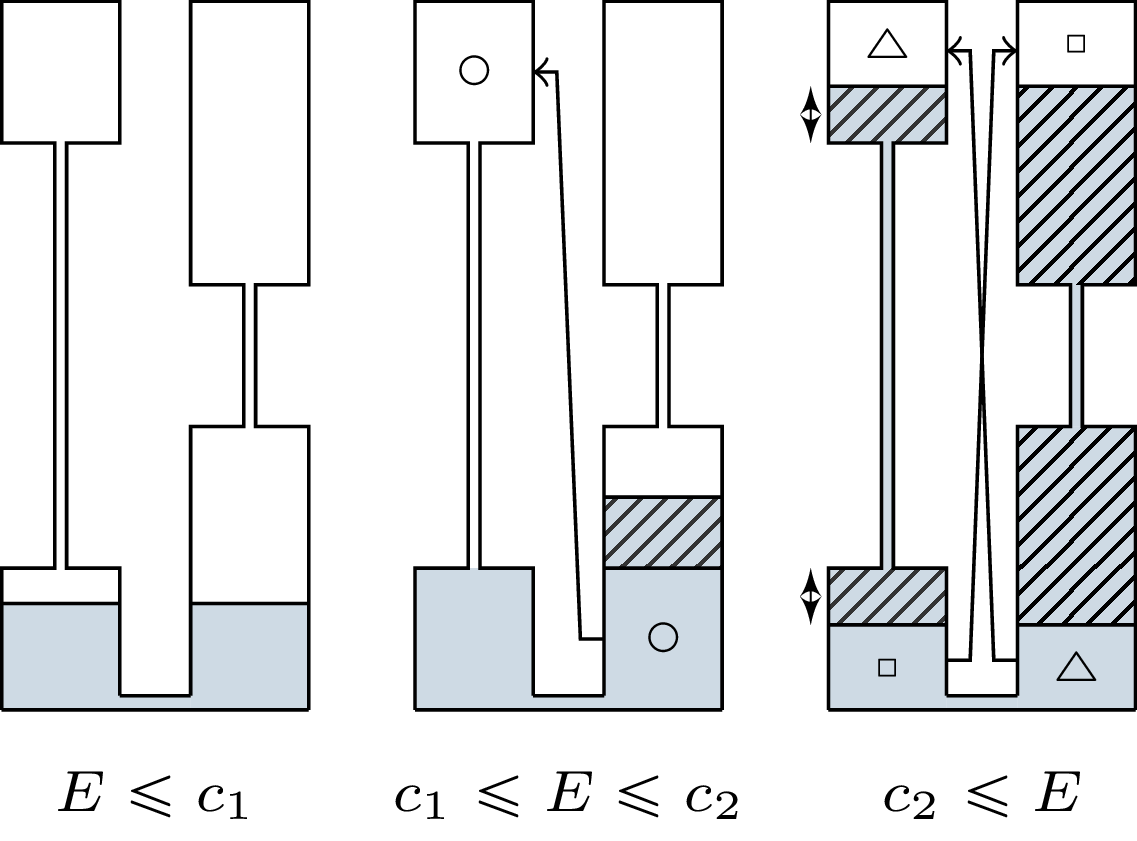
Na poniższych obrazkach zakreskowane pola odpowiadają wartościom \((E-c_1)_+\) oraz \((E-c_2)_+,\) czyli ilości wody, jaka zostanie żonie, jeżeli woda wypełni drugą połowę naczynia. Pola oznaczone tymi samymi symbolami (\(\circ,\) \(\triangle\), \(\square\)) są tej samej wielkości.
Zacznijmy, tak jak w poprzednim artykule, od sytuacji, w której są tylko dwie żony: \((E; c_1, c_2).\) Jak argumentowali w swojej pracy Aumann i Maschler na podstawie innej historii z Talmudu (sporu o ubiór), podział powinien wyglądać następująco. Jeżeli majątek jest większy niż żądanie drugiej żony (czyli \(E > c_2\)), to cała nadwyżka \(E-c_2\) powinna trafić do pierwszej żony. Analogicznie, jeżeli majątek jest większy niż żądanie pierwszej żony (\(E > c_1\)), to \(E-c_1\) powinno trafić do drugiej żony. Całą resztę, czyli sporny kawałek, dzielimy po równo między żony. Używając notacji \((x)_+ = \max \{0,x\},\) otrzymujemy wypłatę żony \(i \in \{1,2\}\): \[x_i = (E-c_j)_+ + \frac{1}{2} \left(E - (E-c_i)_+ - (E-c_j)_+ \right), \mbox{ dla } j = \{1,2\} \setminus \{i\}.\] Podział ten zgadza się z metodą Aumanna i Maschlera, dowód obrazkowy znajduje się na marginesie.
Jak możemy zamodelować tę sytuację z użyciem gier koalicyjnych? Możemy przyjąć, że żony są graczami, i każdej grupie żon (czyli koalicji) przypisać kwotę, jaką może sobie ona zagwarantować. Pierwsza żona sama (bez żadnych negocjacji) potrafi osiągnąć wypłatę \((E-c_2)_+,\) po prostu spłacając całe roszczenie drugiej żony. Analogicznie, druga żona sama może osiągnąć \((E-c_1)_+.\) Razem żony mają do podziału \(E.\) Dostajemy więc następującą grę koalicyjną:
| \(S\) | \(\emptyset\) | \(\{1\}\) | \(\{2\}\) | \(\{1,2\}\) |
|---|---|---|---|---|
| \(f(S)\) | \(0\) | \((E-c_2)_+\) | \((E-c_1)_+\) | \(E\) |
Podstawowym zagadnieniem w grach koalicyjnych jest właśnie pytanie o to, jak podzielić się wspólnie uzyskaną wypłatą: \(f(N).\) Praktycznie wszystkie (rozsądne) metody podziału dla tej gry dają dokładnie taki podział, jaki zdefiniowaliśmy powyżej: każdej żonie dajemy wartość, jaką może osiągnąć sama, a całą resztę dzielimy po równo. Świetnie, tu podejście teoriogrowe daje to, co chcieliśmy uzyskać!
Dużo żon, duży kłopot
A co, kiedy żon jest więcej? Działajmy analogicznie i każdej grupie żon przypiszmy, ile mogłyby sobie zagwarantować, gdyby spłaciły roszczenia reszty. Dla ogólnego problemu bankructwa \((E; c_1, \dots, c_n)\) funkcja \(f\) zdefiniowana jest więc następująco: \[f(S) = (E - \sum_{i~\in N \setminus S} c_i)_+.\] Popatrzmy na grę, jaka powstanie dla problemu bankructwa \((200; 100, 200, 300).\)
| \(S\) | \(\emptyset\) | \(\{1\}\) | \(\{2\}\) | \(\{3\}\) | \(\{1,2\}\) | \(\{1,3\}\) | \(\{2,3\}\) | \(\{1,2,3\}\) |
|---|---|---|---|---|---|---|---|---|
| \(f(S)\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(100\) | \(200\) |
Widzimy, że w tej grze druga i trzecia żona mają symetryczne role – tak jak w podziale \((50, 75, 75)\) opisanym w Talmudzie. Ponadto pierwsza żona ma mniejsze znaczenie, co także się zgadza. Dlatego też wszystkie sensowne metody podziału rozważane w grach koalicyjnych przypiszą pierwszej żonie mniej, a pozostałym dwóm żonom tyle samo. Jak jednak dostać konkretnie te wartości? Wartość Shapleya, która pojawiła się na łamach Delty już kilkakrotnie, przypisałaby pierwszej żonie \(1/6\) majątku. Wartość Banzhafa (po znormalizowaniu) dałaby pierwszej żonie \(1/7\) majątku. Okazuje się natomiast, że \(1/4\) majątku pierwszej żonie i dokładnie taki wynik jak w Talmudzie daje nukleolus!
Wartości Shapleya i Banzhafa to zasadniczo ważona średnia tak zwanych wkładów marginalnych – dla gracza \(i\) w grze \((N,f)\) mamy: \(\sum_{S \subseteq N \setminus \{i\}} \omega_i(S)\)\((f(S \cup \{i\}) - f(S))\)
dla pewnych wag \(\omega_i(S).\) Wartość Shapleya daje podział \((33 \frac{1}{3}, 83 \frac{1}{3}, 83 \frac{1}{3}).\) Wartość Banzhafa daje podział \((25, 75, 75),\) co po znormalizowaniu, aby wartości sumowały się do 200, daje \((28 \frac{4}{7}, 85 \frac{5}{7}, 85 \frac{5}{7}).\)
O nukleolusie pisaliśmy w artykule Jak podzielić lody… \(\Delta^4_{22}\). Dla danego podziału \(x,\) zysk koalicji to jej wypłata pomniejszona o jej wartość w grze: \(e(S,x) = \sum_{i \in S} x_i - f(S).\) Zyski wszystkich koalicji uporządkowane rosnąco tworzą listę zysków. Nukleolus to taki podział wypłaty, dla którego lista zysków jest maksymalna leksykograficznie. Nukleolus stara się zatem zmaksymalizować zysk koalicji, która zyskuje najmniej.
Lista \(a=(a_1,\dots,a_n)\) jest większa leksykograficznie niż lista \(b=(b_1,\dots,b_n),\) jeżeli na pierwszej pozycji, na której listy się różnią, wartość na liście \(a\) jest większa niż na liście \(b.\) Na przykład lista \((1,3,4)\) jest większa niż \((1,2,5).\)
Popatrzmy na zyski koalicji przy podziale \(x=(50, 75, 75)\) (pomijamy koalicję pustą i koalicję wszystkich żon, bo one mają oczywiście zerowy zysk).
| \(S\) | \(\{1\}\) | \(\{2\}\) | \(\{3\}\) | \(\{1,2\}\) | \(\{1,3\}\) | \(\{2,3\}\) | ||
|---|---|---|---|---|---|---|---|---|
| \(e(S,x)\) | \(50\) | \(75\) | \(75\) | \(125\) | \(125\) | \(50\) |
Przykładowo zysk koalicji \(\{2,3\}\) to \(50,\) bo według \(x\) otrzymuje ona \(75+75=150,\) a sama miałaby \(100.\)
Widzimy, że lista zysków to \(L(x) = (50, 50, 75, 75, 125, 125).\) Najmniejszy zysk mają koalicje \(\{1\}\) oraz \(\{2,3\}.\) Czy istnieje podział wypłaty \(y,\) dla którego wektor będzie leksykograficznie większy? Nie, bo przecież jeżeli zmniejszymy wypłatę pierwszej żony \(y_1 < 50,\) to jej zysk spadnie poniżej 50: \(e(\{1\}, y) < 50.\) Z kolei jeżeli zwiększymy \(y_1 > 50,\) to poniżej 50 spadnie zysk koalicji \(\{2,3\}\): \(e(\{2,3\}, y) < 50.\) Musi zatem być \(y_1 = 50\) oraz \(y_2+y_3 = 150.\) Druga i trzecia żona uzyskane 150 muszą podzielić po równo, aby kolejny zysk, jaki pojawia się na liście zysków, nie był mniejszy niż \(75.\)
Jak wygląda nukleolus dla dowolnej liczby żon i dowolnych roszczeń? Okazuje się, że dokładnie tak, jak podział z metody Aumanna i Maschlera. Czemu? To teraz pokażemy.
Wnikliwemu Czytelnikowi zostawiamy sprawdzenie, czy nukleolus dla pozostałych dwóch wariantów omawianych w Talmudzie, czyli problemów bankructwa \((100; 100, 200, 300)\) oraz \((300; 100, 200, 300)\) rzeczywiście daje podziały \((33\frac{1}{3}, 33\frac{1}{3}, 33\frac{1}{3})\) i \((50, 100, 150).\)
Dowód hydroaerobowy
Skupimy się na przypadku, kiedy \(E \le C/2\): jeżeli \(E > C/2,\) to łatwo można wykazać, że nukleolus dla problemu odwrotnego \((C-E; c_1,\dots,c_n)\) jest dopełnieniem nukleolusa dla oryginalnego problemu.
Precyzyjniej, jeżeli \(\hat{x}\) jest nukleolusem dla problemu odwrotnego, to \((c_i - \hat{x}_i)_{i \in N}\) jest nukleolusem dla oryginalnego. Aby to pokazać, w poniższym dowodzie wystarczyłoby zamienić wodę z powietrzem.
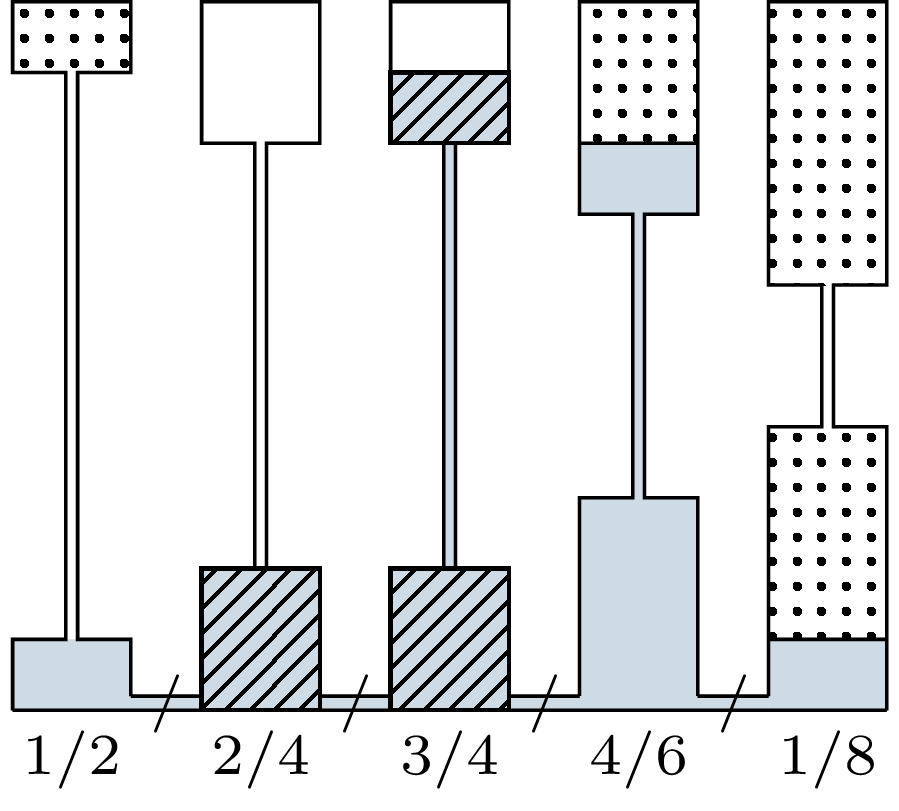
Dla problemu bankructwa \((10; 2, 4, 4, 6, 8)\) poniższy układ hydrauliczny prezentuje podział \(y=(1, 2, 3, 4, 1).\) Zysk koalicji \(S=\{2,3\}\) to \(e(S,y) = 5,\) jest to bowiem koalicja wodna: ilość wody w naczyniach żon z \(S\) (zakreskowany obszar) jest mniejsza niż ilość powietrza w pozostałych naczyniach (zakropkowany obszar). Koalicją powietrzną jest np. \(S = \{3,4,5\}.\)
Weźmy dowolny podział \(x.\) Zablokujmy rurki łączące naczynia w systemie hydraulicznym i wlejmy wodę tak, aby odpowiadała podziałowi \(x.\) Czym jest teraz zysk koalicji \(S\)? Mamy dwa przypadki. Koalicję \(S\) nazwiemy wodną, jeżeli majątek nie przekracza roszczenia żon spoza \(S\): \(E \le \sum_{i \in N \setminus S} c_i.\) Mamy wówczas \(f(S) = 0\) i zysk tej koalicji jest równy ilości wody w naczyniach żon z \(S\): \(e(S,x) = \sum_{i \in S} x_i.\) Koalicję nazwiemy powietrzną, jeżeli majątek jest nie mniejszy niż roszczenia pozostałych żon: \(E \ge \sum_{i \in N \setminus S} c_i.\) Jak pokazują poniższe obliczenia, zysk tej koalicji jest natomiast równy ilości powietrza w naczyniach pozostałych żon: \[e(S,x) = \sum_{i~\in S} x_i - f(S) = (E - \sum_{i~\in N \setminus S} x_i) - (E - \sum_{i~\in N \setminus S} c_i) = \sum_{i~\in N \setminus S} (c_i-x_i).\] Jak poznać, jakiego typu jest koalicja \(S\)? Musimy sprawdzić, czy cała woda zmieściłaby się w naczyniach żon spoza \(S.\) W tym celu dla dowolnego ułożenia wody w naczyniach wystarczy porównać ilość wody w naczyniach żon z \(S\) oraz ilość powietrza w pozostałych naczyniach. Jeżeli wody jest mniej niż powietrza, to woda się mieści, więc mamy koalicję wodną. Jeżeli powietrza jest mniej niż wody, to woda się nie mieści, i mamy koalicję powietrzną. Jeżeli jest tyle samo, to koalicja jest wodno-powietrzna (i wodna, i powietrzna).
Wnioskiem z naszej analizy jest zatem fakt, że zysk koalicji jest mniejszą z wartości ,,ilość wody w naczyniach żon z koalicji” oraz ,,ilość powietrza w naczyniach pozostałych żon”: \(e(S, x) = \min \Bigl\{\sum_{i \in S} x_i,\) \(\sum_{i \in N \setminus S} (c_i-x_i)\Bigr\}.\)
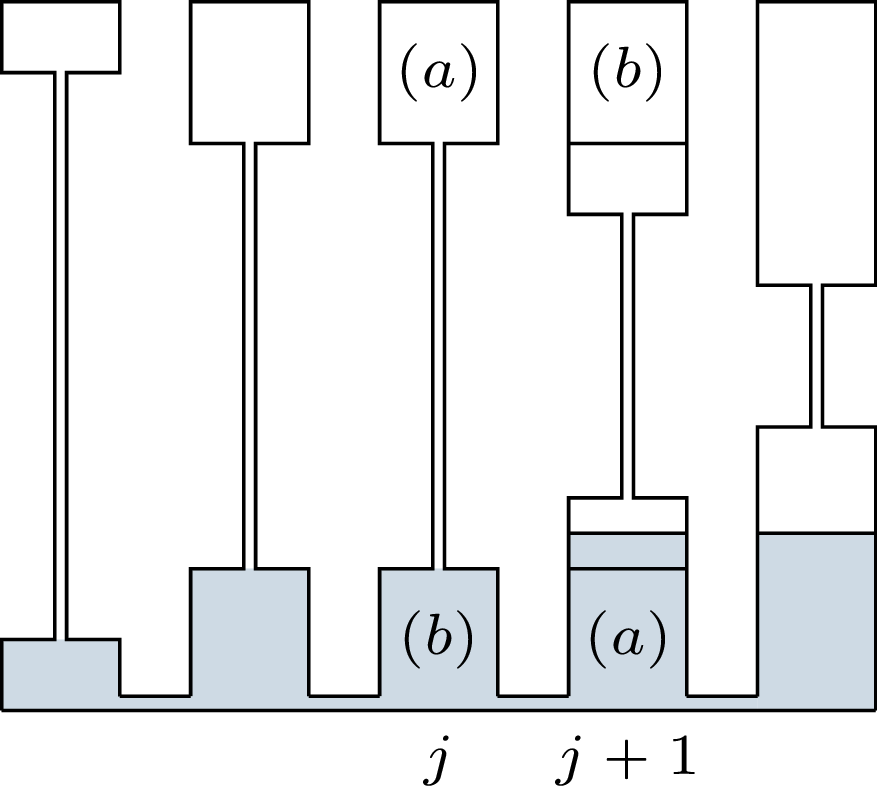
Niech teraz \(x\) będzie podziałem z metody Aumanna i Maschlera, a \(y\) dowolnym innym podziałem. Udowodnimy, że lista zysków dla \(y\) jest leksykograficznie mniejsza niż dla \(x.\) Niech \(j\) będzie pierwszą pozycją, na której oba podziały się różnią. Zastanówmy się, które koalicje \(S\) przy podziale \(x\) mają zysk mniejszy niż \(x_j\)?
Jeżeli \(S\) jest koalicją wodną, to aby jej zysk był mniejszy niż \(x_j,\) nie może ona zawierać żony \(j\) ani żadnej kolejnej (bo \(x_k\ge x_j\) dla \(k>j\)). Stąd wniosek, że \(S\) jest podzbiorem \(\{1,\dots,j-1\}\) i jej zysk według \(x\) i \(y\) jest taki sam.
Jeżeli \(S\) jest koalicją powietrzną, to aby jej zysk był mniejszy niż \(x_j,\) to ani \(j,\) ani żadna kolejna żona nie może być poza \(S.\) Stąd wniosek, że \(S\) zawiera \(\{j,\dots,n\}\) oraz podzbiór \(\{1,\dots,j-1\}\) i też ma taki sam zysk według \(x\) i \(y.\)
Ta analiza pokazuje, że każda koalicja, która ma mniejszy zysk niż \(x_j\) według podziału \(x,\) ma identyczny zysk według podziału \(y.\) Aby wykazać, że lista zysków dla \(y\) jest leksykograficznie mniejsza niż dla \(x,\) wskażemy koalicję, która według \(y\) ma mniejszy zysk niż \(x_j,\) a według \(x\) nie.
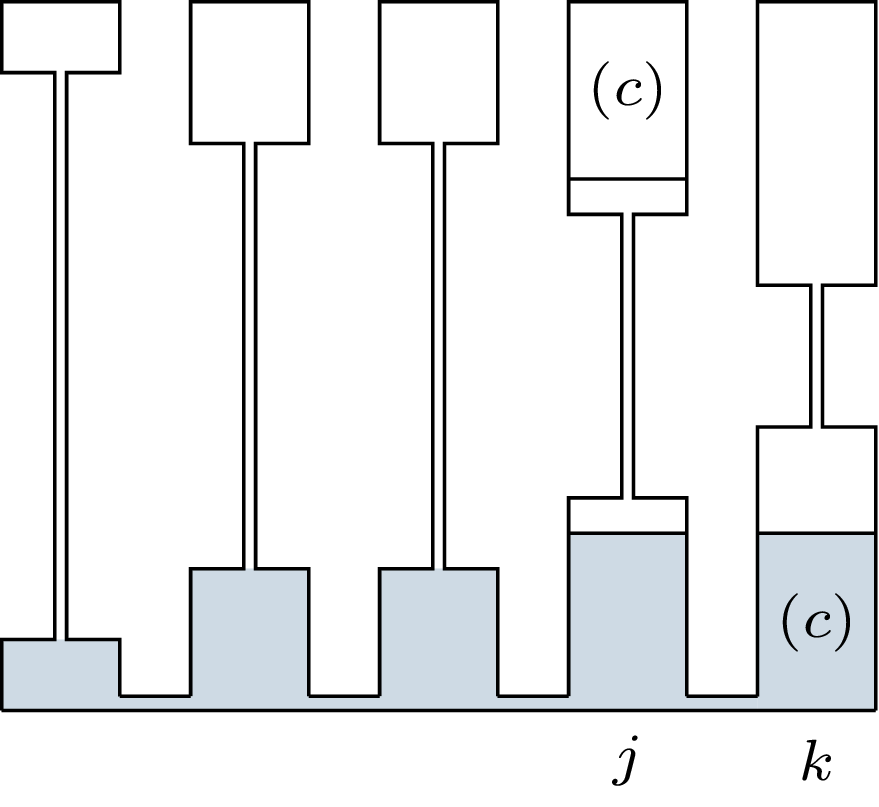
Podział \(x,\) jaki dostaniemy z powyższego \(y,\) jeżeli odblokujemy rurki łączące naczynia. Pierwszą pozycją, na której podziały się różnią, jest \(j=3.\) Obszary oznaczone \((a)\) i \((b)\) pokazują, że koalicje \(\{j\}\) oraz \(N \setminus \{j\}\) są odpowiednio wodne i powietrzne.
Gdyby podział \(y\) różnił się na kolejnej pozycji (np. \(y = (1,2,2,2,3)\)), to kluczowy jest fakt, że wodną koalicją jest \(\{k\},\) co pokazują obszary \((c).\)
Jeżeli \(x_j = c_j/2\) oraz \(y_j < x_j,\) to taką koalicją jest \(\{j\}.\) Jest to koalicja wodna, co łatwo zobaczyć, odblokowując rurki łączące naczynia, czyli w podziale \(x\): ilość wody w jej naczyniu jest wówczas mniejsza bądź równa ilości powietrza w naczyniu kolejnej żony. Jej zysk to zatem \(y_j < x_j.\)
Jeżeli \(x_j = c_j/2\) oraz \(y_j > x_j,\) to taką koalicją jest \(N \setminus \{j\}.\) Ta koalicja na pewno jest bowiem koalicją powietrzną: ponownie odblokowując rurki, widzimy, że w podziale \(x\) kolejna żona sama ma co najmniej tyle wody, ile powietrza ma żona \(j.\) Jej zysk to zatem \(c_j - y_j < x_j.\)
W końcu jeżeli \(x_j < c_j/2,\) to \(j\)-ta żona i wszystkie kolejne dostają w \(x\) tyle samo: \(x_j.\) Skoro \(y\) różni się od \(x\) dopiero na pozycji \(j\)-tej, to \(j\) albo któraś z dalszych żon, powiedzmy \(k,\) musi dostawać mniej niż \(x_j.\) Wówczas szukaną koalicją jest \(\{k\}\): jest to koalicja wodna, bo według podziału \(x\) woda z jej naczynia nawet nie dopełni naczynia \(j\)-tej żony (lub kolejnej, jeżeli \(j=k\)). Jej zysk to zatem \(y_k < x_j.\)
To kończy dowód.
Dowód na podstawie artykułu:
Benoit, Jean-Pierre, “The nucleolus is contested-garment-consistent: a direct proof”, Journal of Economic Theory 77.1 (1997): 192–196.
Czy autorzy Talmudu znali pojęcie gier koalicyjnych i nukleolusa? Jest to raczej mało prawdopodobne. Niewątpliwie udało im się jednak wpłynąć na rozwój teorii gier koalicyjnych, mimo że (zgodnie z dostępną aktualnie wiedzą) powstała ona dwa tysiące lat później.