Odpowiedź: Tak.
Zaznaczmy bieguny \(N\) (północny) i \(S\) (południowy) na planecie i niech punkty \(A,\) \(B,\) \(C\) i \(D\) podzielą odpowiedni równik na cztery równe łuki, jak na rysunku.
Rozważmy zamkniętą ścieżkę \[A \mapsto B\mapsto S\mapsto D \mapsto C \mapsto N
\mapsto A\] wzdłuż powierzchni, składającą się z łuków wielkich kół planety.
Ta ścieżka składa się z 6 identycznych łuków równych \(\frac{1}{4}\) równika, więc
długość ścieżki jest równa \(600\) km.
Pokażemy teraz, że dla każdego punktu planety istnieje na tej ścieżce punkt
oddalony od niego o nie więcej niż 50 km. Podzielmy powierzchnię planety na
\(8\) identycznych trójkątów sferycznych z wierzchołkami w zaznaczonych punktach.
Łazik odwiedził wszystkie wierzchołki i wszystkie punkty co najmniej jednego
boku każdego trójkąta.
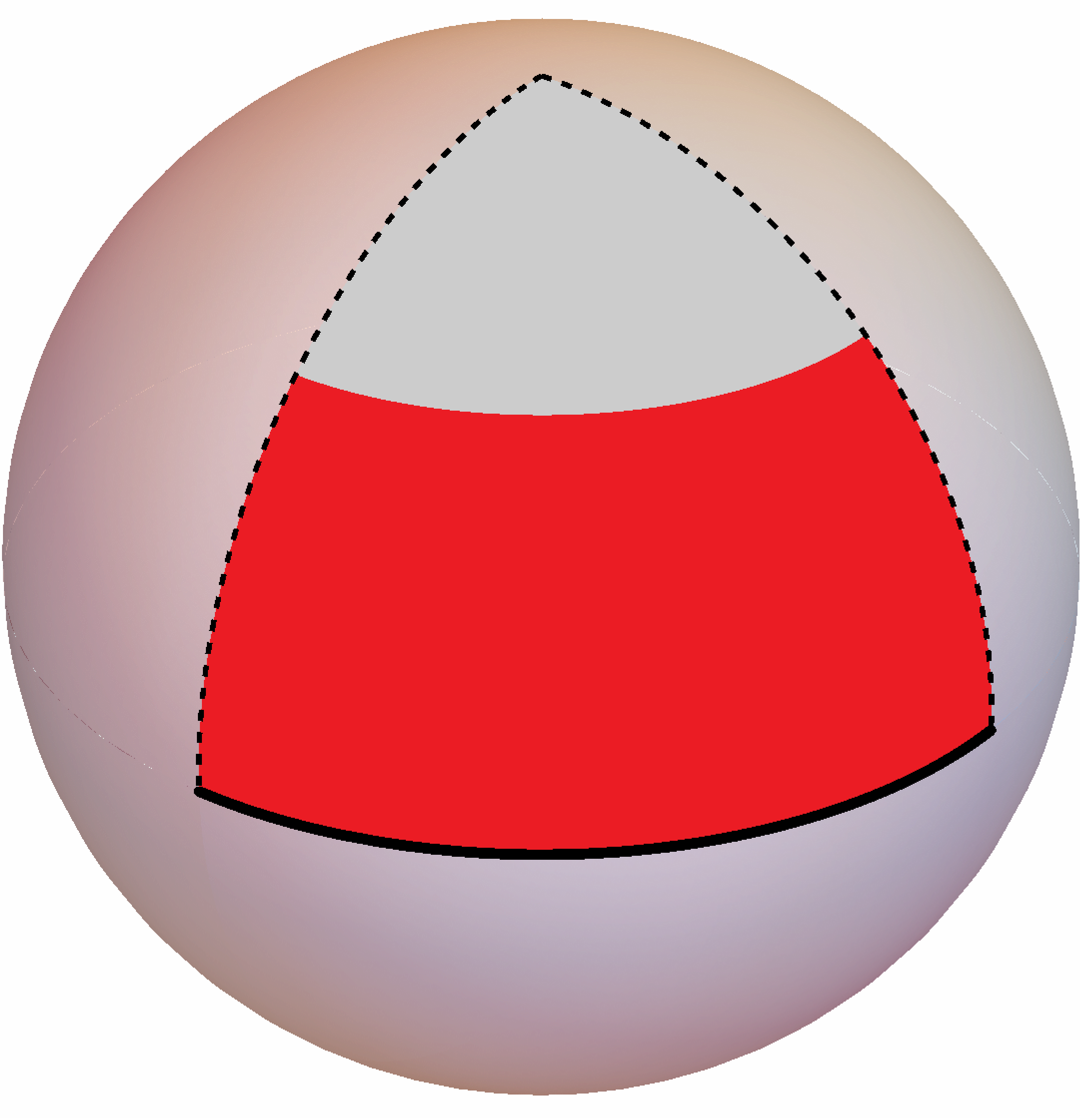
Rozważmy jeden taki trójkąt, jak na rysunku niżej. Jego bok ma długość 100 km.
Czerwona część tego trójkąta została zbadana przez łazik księżycowy, ponieważ podróżował
on wzdłuż wyróżnionego boku, a szara część
została zbadana, ponieważ odwiedził on przeciwległy wierzchołek. To samo
rozumowanie dla dowolnego innego trójkąta podziału dowodzi, że podana ścieżka
spełnia warunki zadania.