* Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Maria Donten-Bury była redaktorką Delty w latach 2009–2014.
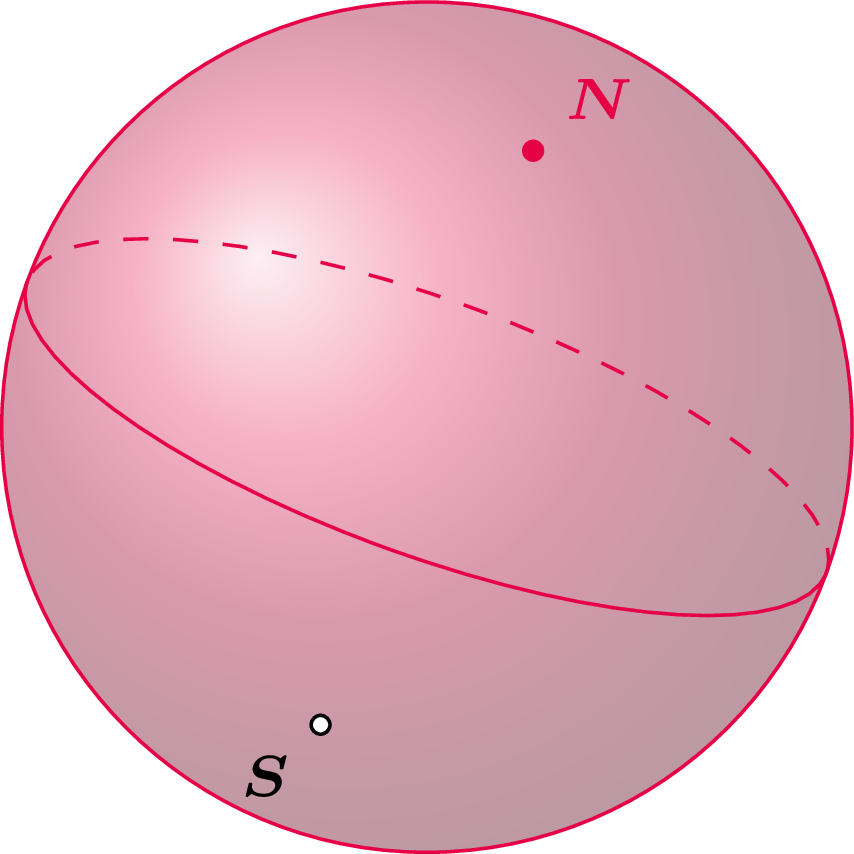
Wyprawa na biegun północny. Wyobraźmy sobie podróżników na powierzchni Ziemi wyposażonych w kompasy wskazujące północ (przyjmijmy, że północ magnetyczna i geograficzna to to samo i że nie ma żadnych lokalnych anomalii). Wskazania kompasów w okolicach biegunów północnego \(N\) i południowego \(S\) pokazują rysunki na marginesie. Każdy z podróżników chce dotrzeć na biegun północny. Jeśli podróżnik nie znajduje się akurat na biegunie, to wie, co ma robić: wędruje wzdłuż południka, na którym się znajduje, zgodnie ze wskazaniem kompasu. Ale na biegunie kompas jest bezużyteczny, bo nie pokazuje jednego kierunku – bieguny są punktami krytycznymi dla zadania podróżnika. Mimo to podróżnik będący na biegunie północnym umie poradzić sobie z zadaniem: po prostu stoi w miejscu.
W ten sposób zadanie dotarcia do bieguna i sam proces podróży dają nam podział powierzchni Ziemi (którą matematyk widzi jako sferę) na części, nazywane komórkami. Jedna to prawie cała sfera wraz z punktem \(N\), druga jest jednopunktowa i składa się z bieguna \(S\). Zauważmy, że komórki są w pewnym sensie prostsze niż wyjściowa sfera: ta większa komórka to właściwie płaszczyzna, tylko trochę wygięta.
Twierdzenie o rozkładzie. Powyższy przykład wygląda na łatwy, ale Czytelnik może sobie wyobrazić, że jeśli zamiast sfery próbujemy podzielić na proste kawałki przestrzeń o mniej oczywistej strukturze, to problem robi się znacznie ciekawszy. Dla pewnej klasy przestrzeni rozwiązaniem jest twierdzenie Andrzeja Szczepana Białynickiego-Biruli o rozkładzie, które można wypowiedzieć jednym zdaniem:
Jeśli pogrupujemy punkty rozmaitości \(X\) względem granic przy działaniu grupy \(\mathbb{K}^*\), to otrzymamy zaskakująco ładne i mniej skomplikowane podrozmaitości.
To, że \(X\) jest rozmaitością, znaczy, że w bliskiej okolicy każdego swojego punktu przypomina zwykłą przestrzeń euklidesową: prostą, płaszczyznę, przestrzeń trójwymiarową… być może trochę zakrzywioną. Taką strukturę mają na przykład okrąg, sfera, powierzchnia torusa, ale też bardziej skomplikowane formy, jak przestrzeń rzutowa (o której za chwilę).
Oprócz rozmaitości mamy grupę, czyli zbiór elementów, na których możemy wykonywać pewne działanie oraz je odwracać. Na przykład grupę \(\mathbb{R}^*\) niezerowych liczb rzeczywistych, które da się mnożyć i dzielić. Taka grupa działa na pewnej rozmaitości, jeśli każdy jej element coś robi z punktami rozmaitości, jakoś je przestawia. Co więcej, te przestawienia mają być zgodne z mnożeniem w grupie, ale tu nie będziemy potrzebowali tego dokładnie wyjaśnić.
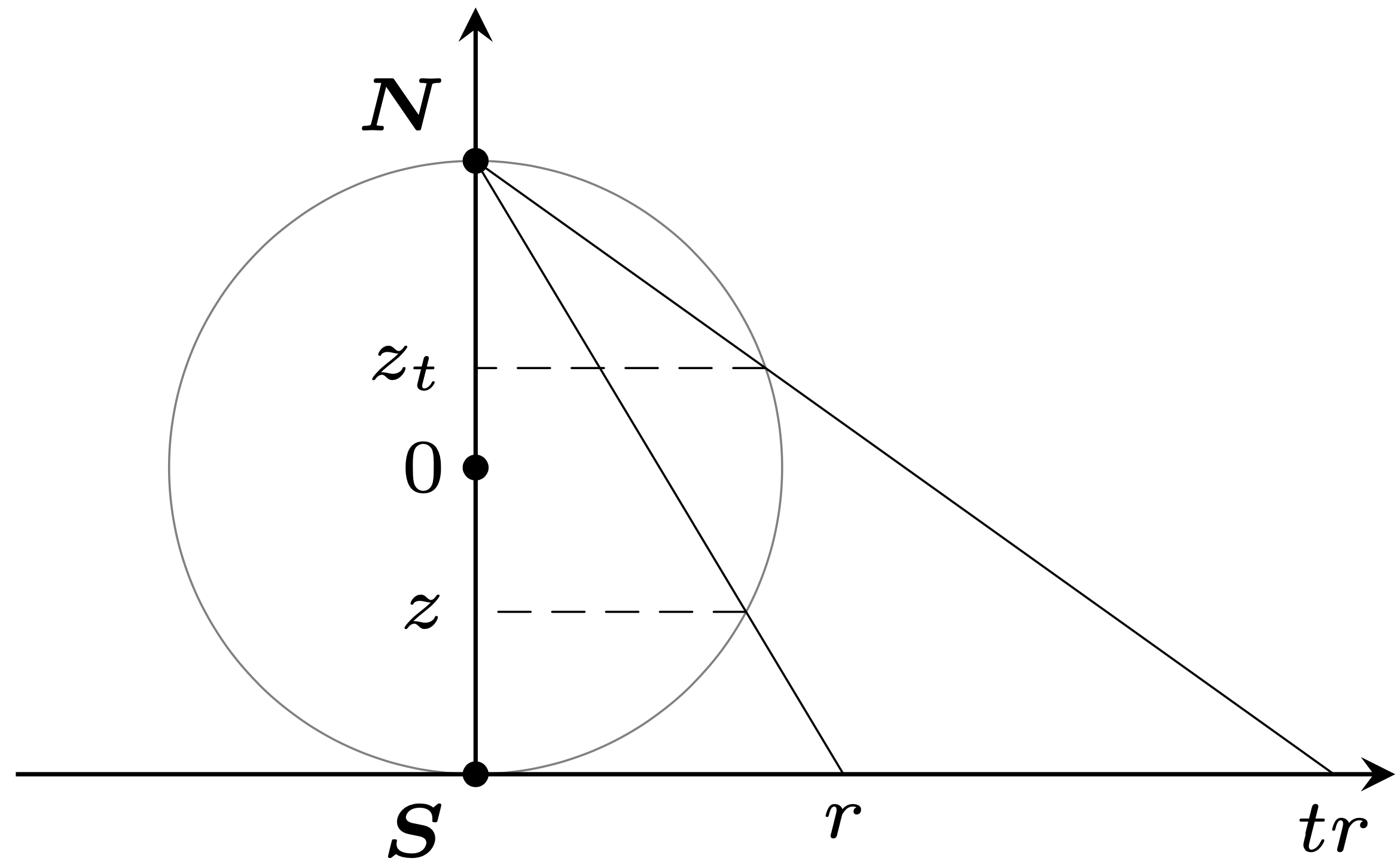
Spróbujmy w tym języku opowiedzieć o wyprawie na biegun północny. Jak zwykle, zamiast o powierzchni Ziemi myślimy o sferze \(S^2\) zanurzonej w trójwymiarowej przestrzeni \(\mathbb{R}^3\). Opiszmy tę sferę równaniem \({x^2 + y^2 + z^2 = 1}\). Działa na niej grupa \(\mathbb{R}^*\) w następujący sposób. Trzecią współrzędną punktu na sferze możemy zapisać jako \(z = \frac{r^2-4}{r^2+4}\) dla pewnego \(r \in \mathbb{R}\). Wtedy liczbie \(t \in \mathbb{R}^*\) przypiszemy przekształcenie \(S^2\), które przesuwa punkt wzdłuż południka do punktu o trzeciej współrzędnej \(z_t = \frac{t^2r^2 - 4}{t^2r^2+4}\). Skąd te wzory? Pochodzą od mnożenia przez liczby z \(\mathbb{R}^*\), jeśli najpierw rozprostujemy południk przekształceniem odwrotnym do rzutu stereograficznego. Geometryczny charakter przedstawionych zależności prezentuje rysunek na marginesie.
Oczywiście współrzędne \(x\) i \(y\) też się zmienią – w taki sposób, żeby podróżnik został na tej samej długości geograficznej – ale nie potrzebujemy znać dokładnie ich nowych wartości. Zauważmy jeszcze, że bieguny moglibyśmy (niezbyt ściśle) opisać, w miejsce \(r\) wstawiając \(0\) oraz \(\infty\).
Twierdzenie o rozkładzie mówi o grupowaniu punktów \(S^2\) względem granic przy działaniu \(\mathbb{R}^*\). Możemy zapisać \(z_t = \frac{r^2 - 4/t^2}{r^2+4/t^2}\), skąd widać, że dla każdego \(r\neq 0\) (czyli \(z\neq -1\)) jeśli \(t\) dąży do \(\infty\), to \(z_t\) dąży do 1. A jedyny punkt na sferze, w którym \(z = 1\), to biegun \(N\). Wobec tego grupowanie punktów \(S^2\) względem granic przy badanym działaniu wyodrębnia, jak przewidzieliśmy, dużą komórkę złożoną z całej sfery oprócz bieguna \(S\), dla której granicą jest biegun \(N\). Druga komórka jest jednopunktowa, złożona z bieguna \(S\), który jest swoją własną granicą przy działaniu \(\mathbb{R}^*\), czyli tak zwanym punktem stałym.
Granice, których… brakuje. Jak widać, granice przy działaniu grupy są kluczowym elementem twierdzenia o rozkładzie. W powyższym przykładzie mieliśmy szczęście, i udało nam się je dość łatwo obliczyć. Spójrzmy teraz na sytuację, która pomoże nam lepiej zdefiniować granice przy działaniu grupy w ogólnym przypadku.
Niech \(\mathbb{K}= \mathbb{R}\) i określmy działanie \(\mathbb{R}^*\) na płaszczyźnie \(\mathbb{R}^2\) wzorem \[\label{eq:actionR2} \tag{$\star$} t\circ (x, y) := (t^{-1}x, ty),\] gdzie \(t\in \mathbb{R}^*\). Jaka jest granica punktu \((x,y)\) przy tak określonym działaniu? Jeśli \(y=0\), to sprawa jest prosta: \[\lim_{t\to \infty} t\circ (x, y) = \lim_{t\to \infty} (t^{-1}x, ty) = \lim_{t\to \infty} (t^{-1}x, 0) = (0,0).\] Ale jeśli \(y \neq 0\), to ta granica nie istnieje na płaszczyźnie… Fakt, że czasem tak się dzieje, jest irytujący. Mamy kłopot, ponieważ użyliśmy płaszczyzny \(\mathbb{R}^2\), której brakuje ,,punktów w nieskończoności”. Problem ten odczuwało już wielu matematyków i istnieje standardowe lekarstwo: zamiast płaszczyzny \(\mathbb{R}^2\) powinniśmy rozważyć płaszczyznę rzutową.
Płaszczyzna rzutowa to wersja płaszczyzny z ,,wbudowaną nieskończonością”. W Delcie o niej nie raz już była mowa – po krótki opis można sięgnąć do \(\Delta^{4}_{19}\), ale lepiej poznać ją z różnych punktów widzenia w \(\Delta^5_{13}\). Tutaj zdefiniujemy ją jako zbiór punktów \(\mathbb{R}^3\setminus \{(0,0,0)\}\) (tak!), gdzie utożsamiamy punkty \((x_0, y_0, z_0)\) oraz \((x_1, y_1, z_1)\), jeśli są proporcjonalne, czyli istnieje taka liczba \(\lambda\in \mathbb{R}^*\), że \(x_1 = \lambda x_0\), \(y_1 = \lambda y_0\), \(z_1 = \lambda z_0\). Klasę tak utożsamionych punktów oznaczamy przez \((x_0 : y_0 : z_0)\), a zbiór wszystkich tych klas to właśnie płaszczyzna rzutowa, oznaczana jako \(\mathbb{R}\mathbb{P}^2\). Dodajmy, że z przedstawionej definicji wynika, iż \({(x_0 : y_0 : z_0) = (\lambda x_0 : \lambda y_0 : \lambda z_0)}\) dla każdej niezerowej liczby \(\lambda\).
Definicję na klasach punktów można ująć w zgrabnej formie: \[\mathbb{R}\mathbb{P}^2 := (\mathbb{R}^3 \setminus \{(0,0,0)\}) / \mathbb{R}^*.\]
Z tej definicji nie widać jednak zupełnie, dlaczego \(\mathbb{R}\mathbb{P}^2\) nazywa się płaszczyzną rzutową. Otóż w każdej klasie \((x_0 : y_0 : z_0)\in \mathbb{R}\mathbb{P}^2\), gdzie \(z_0 \neq 0\), jest dokładnie jeden punkt z ostatnią współrzędną równą 1 – to \((x_0/z_0, y_0/z_0, 1)\). Możemy więc utożsamić zbiór \[U := \left\{ (x_0: y_0: z_0)\in \mathbb{R}\mathbb{P}^2\ |\ z_0\neq 0 \right\}\] ze zbiorem \(\mathbb{R}^2\), gdzie punktowi \((x_0: y_0: z_0)\in \mathbb{R}\mathbb{P}^2\) odpowiada \({(x_0/z_0, y_0/z_0)\in \mathbb{R}^2}\). Pozostałe punkty \(\mathbb{R}\mathbb{P}^2\), te postaci \((x_0 : y_0 : 0)\), uważamy za dodane do płaszczyzny \(U\) punkty w nieskończoności.
Wracając do naszego przykładu, możemy zdefiniować działanie \(\mathbb{R}^*\) na \(\mathbb{R}\mathbb{P}^2\) poprzez \(t\circ (x:y:z) = (t^{-1}x : ty : z)\). Jeśli popatrzymy na \(U\), to \({t\circ (x:y:1) = (t^{-1}x : ty : 1)}\), co dokładnie zgadza się ze wzorem \((\star)\), którym powyżej definiowaliśmy działanie na \(\mathbb{R}^2\). Teraz wreszcie możemy znaleźć granicę dowolnego punktu przy tak ustalonym działaniu. Mianowicie, jeśli weźmiemy \((x:y:z)\in \mathbb{R}\mathbb{P}^2\), gdzie \(y\neq 0\), to \[\begin{aligned} \lim_{t\to \infty} t\circ(x:y:z) &=\lim_{t\to \infty} (t^{-1}x : ty : z) = \lim_{t\to \infty} (t^{-1}\cdot t^{-1}\cdot x : t^{-1}\cdot ty : t^{-1}z) =\\ &=\lim_{t \to \infty} (t^{-2}x : y : t^{-1}z) = (0 : y : 0) = (0 : 1 : 0). \end{aligned}\]
Prościej można obliczyć granicę punktu \((x:0:z)\in \mathbb{R}\mathbb{P}^2\), gdzie \(z\neq 0\): \[\lim_{t\to \infty} t\circ(x:0:z) = \lim_{t\to \infty}(t^{-1}x : 0 : z) = (0 : 0 : z) = (0 : 0 : 1).\] Ostatni nierozważony jeszcze punkt \(\mathbb{R}\mathbb{P}^2\) to \((1:0:0)\). Ale w tym przypadku \(t\circ(1:0:0) =\) \((t^{-1}:0:0) = (1:0:0)\), czyli mamy punkt stały działania.
Jak wobec tego wygląda pogrupowanie punktów względem granic przy działaniu \(\mathbb{R}^*\)? Zbiór punktów takich, że \(y\neq 0\), których granicą jest \((0 : 1 : 0)\), można utożsamić z płaszczyzną \(\mathbb{R}^2\) (podobnie jak powyżej punkty, dla których \(z \neq 0\)). Zbiór punktów takich, że \(y = 0\), ale \(z\neq 0\), dla których granicą jest \((0 : 0: 1)\), utożsamia się z prostą \(\mathbb{R}\). Ostatni zbiór składa się z punktu \((1 : 0 : 0).\) Otrzymaliśmy więc podział płaszczyzny rzutowej na bardzo ładne części – ładne w tym przypadku oznacza, że można je utożsamić z \(\mathbb{R}^{n}\) dla pewnego \(n\), zależnego od granicy.
Tytułowe twierdzenie, które wreszcie możemy dokładnie sformułować, mówi, że to samo będzie się działo dla każdego (algebraicznego) działania na każdej gładkiej podrozmaitości w każdej przestrzeni rzutowej (nie tylko na płaszczyźnie). Teraz zamiast \(\mathbb{R}\) będziemy dla większej ogólności pisać \(\mathbb{K}\), bo twierdzenie działa nie tylko dla ciała liczb rzeczywistych. Ustalmy też różne liczby całkowite \(a_0, \ldots ,a_n\) i zdefiniujmy działanie \(\mathbb{K}^*\) na \(\mathbb{K}\mathbb{P}^n\) wzorem \[t\circ (x_0 : x_1 : \ldots : x_n) = (t^{a_0}x_0 : t^{a_1}x_1 : \ldots : t^{a_n}x_n).\] Zbiór punktów o ustalonej granicy \(p\) nazywamy (ujemną) komórką Białynickiego-Biruli stowarzyszoną z \(p\).
Co by było, gdyby te liczby nie były różne?
Istnieją też dodatnie komórki zdefiniowane podobnie, ale gdy granicę bierze się przy \(t\to 0\).
Twierdzenie (ASBB, 1973). Niech \(X\subseteq \mathbb{K}\mathbb{P}^n\) będzie gładką podrozmaitością taką, że \(\mathbb{K}^* \circ X \subseteq X\), czyli działanie nie wyprowadza punktów \(X\) poza \(X\). Wtedy każda komórka Białynickiego-Biruli w \(X\) jest izomorficzna z przestrzenią liniową \(\mathbb{K}^{n_i}\) dla pewnego \(n_i\in \mathbb{N}\) zależnego od komórki.
Inne ciała. Jak wspomnieliśmy powyżej, nie korzystamy z żadnych szczególnych własności ciała liczb rzeczywistych. Analiza przykładu przebiegałaby właściwie tak samo, gdyby za \(\mathbb{R}\) wszędzie podstawić \(\mathbb{Q}\). Ba, ten argument działa nawet, jeśli zamiast \(\mathbb{R}\) wybierzemy ciało liczb zespolonych \(\mathbb{C}\) lub ciało \(\mathbb{Z}_p\), które ma \(p\) elementów, dla liczby pierwszej \(p\). Musimy jedynie zachować konwencję, że \(\lim\limits_{t\to \infty} t^{-n} x\) jest równe zero dla każdego naturalnego \(n > 0\) i każdego \(x\) z \(\mathbb{C}\) czy \(\mathbb{Z}_p\). To wiedzie do paradoksalnego, ale słusznego wniosku, że używane powyżej pojęcie granicy nie wymaga żadnej ,,ciągłości”! Przykładowo, Czytelnik może obliczyć, że \(\mathbb{Z}_2\mathbb{P}^2\) składa się jedynie z siedmiu punktów: \[(0:0:1),\ (0:1:1),\ (1:0:1),\ (1:1:1),\ (1:0:0),\ (0:1:0),\ (1:1:0),\] a mimo to równość \(\lim\limits_{t\to \infty} t\circ(1:1:1) = (0:1:0)\) dla działania z naszego przykładu nadal zachodzi.
Ilustracja płaszczyzny rzutowej \(\mathbb{Z}_2\mathbb{P}^2\)
Gładkość. Komórki Białynickiego-Biruli można też zdefiniować w ogólniejszym przypadku, bez zakładania gładkości. Ustalmy tylko \(X\subseteq \mathbb{K}\mathbb{P}^n\) spełniający \(\mathbb{K}^* \circ X \subseteq X.\) Wtedy definiujemy \(X^+\) jako zbiór wszystkich \(\mathbb{K}^*\)-niezmienniczych odwzorowań z \(\mathbb{K}\) do \(X.\) Nie jest jasne, dlaczego na tak określonym zbiorze da się zbudować strukturę przestrzeni. Dopiero W. Drinfeld w roku 2013 dowiódł, że to możliwe. Przestrzeń ta okazała się bardzo użyteczna w badaniu przypadku odległego od gładkiego – w tzw. przestrzeniach moduli. Ale to już temat na inny artykuł.
Zakończenie. Chcielibyśmy zakończyć niniejszy artykuł fragmentem odpowiedzi Andrzeja Szczepana Białynickiego-Biruli na pytanie o pożytki z powszechnego nauczania matematyki, będące częścią przeprowadzonej przez Deltę ankiety (\(\Delta^{10}_{95}\)):
Andrzej Szczepan Białynicki-Birula zmarł w 2021 r. Od 2022 r. działa Fundacja Jego imienia, wspierająca studentów matematyki i informatyki UW z Białorusi i Ukrainy:
www.mimuw.edu.pl/~fundacja_asbb
(…) roli matematyki nie można sprowadzać do znajomości wzorów i faktów. Sądzę, że ważna jest szkoła myślenia, którą daje matematyka każdemu, pewna dyscyplina formułowania i wypowiadania poglądów i argumentów. Brak takiej dyscypliny może bardzo w życiu przeszkadzać.
Na trzech stronach tego artykułu przebyliśmy dość daleką drogę – od wprowadzającego przykładu o podróżnikach na sferze do analizy bardzo abstrakcyjnych struktur. Mamy nadzieję, że lektura była dla Czytelników dobrym treningiem wspomnianego wyżej matematycznego myślenia.