Jeszcze o taliach

* Twórca Delty, w latach 1974–2018 jej redaktor naczelny

W znakomitym artykule O wieszaniu bombek na choince, \(\Delta_{11}^{12}\), Krzysztof Rudnik definiuje talie: talia jakiejś bryły to najmniejszy okrąg otaczający ją i niedający się z niej zsunąć. Kluczowymi bohaterami opowieści są foremne antygraniastosłupy.

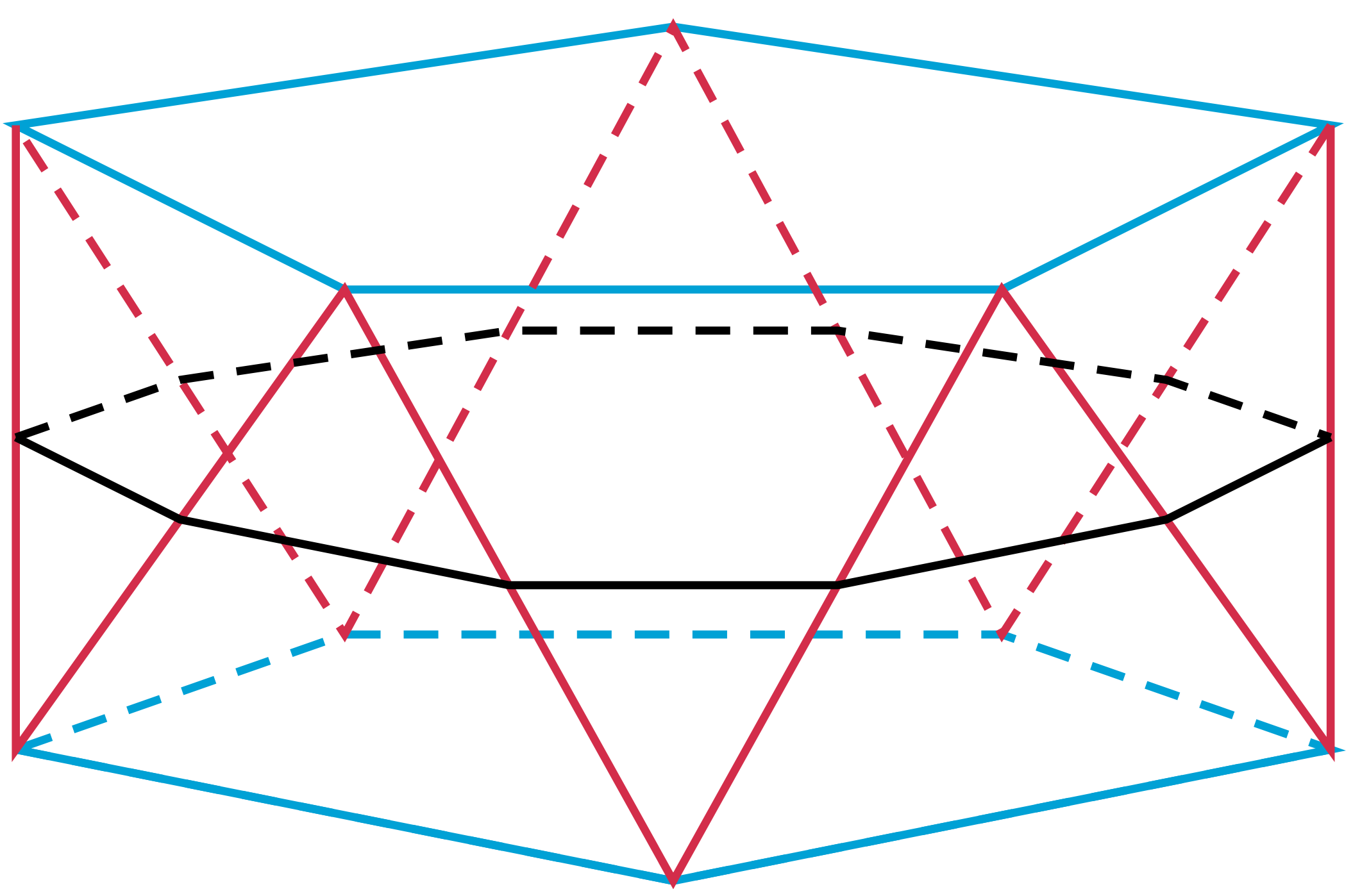
Antygraniastosłup to bryła ograniczona przez dwa jednakowe wielokąty foremne (podstawy) leżące w płaszczyznach równoległych i nieco względem siebie obrócone, tak by można je było połączyć paskiem trójkątów równoramiennych (a nie, tak jak w graniastosłupie, prostokątami), które też antygraniastosłup ograniczają. Antygraniastosłup jest foremny, gdy trójkąty mają wszystkie boki tej samej długości co jego podstawy. Obok narysowany jest 5-antygraniastosłup foremny. Jego talia to okrąg opisany na przecięciu tego antygraniastosłupa płaszczyzną równoległą do jego podstaw i w tej samej od nich odległości – przecięciem tym jest dziesięciokąt foremny o boku (przy naszej przedstawionej na marginesie umowie) \({1\over 2}.\)

W tym tekście występować będą wielościany mające wszystkie krawędzie równej długości, niech to będzie 1.

Co więcej – tak samo otrzymujemy talie dowolnego \(n\)-antygraniastosłupa foremnego: są to okręgi opisane na \(2n\)-kątach foremnych o boku \({1\over 2}.\) To śmiała teza i wypadałoby jej dowieść. Tym bardziej że wszystkie przekroje danego antygraniastosłupa płaszczyznami równoległymi do podstaw mają obwód tej samej długości. Czemu więc obręcz nałożona na ,,środkowy” przekrój nie miałaby się zsunąć?

Argumentem uzasadniającym ten fakt jest spostrzeżenie, że spośród otrzymanych w przecięciach wielokątów najmniejszy okrąg opisany ma ten, który ma boki jednakowej długości. Miłośnicy rachunków zapewne potrafią to obliczyć, ale my obejrzymy to dla 3-antygraniastosłupa, czyli (prawda?) ośmiościanu foremnego, gdzie talia jest sześciokątem (przy większej liczbie boków różnica między wielokątem foremnym a okręgiem jest mało widoczna).

Zwróćmy jeszcze uwagę na fakt, że antygraniastosłup leży w całości po jednej stronie płaszczyzny każdego ograniczającego go wielokąta, więc (jako przecięcie półprzestrzeni) jest wypukły. Może zatem dziwić, że bryła wypukła ma talię, choć… (ale o tym potem).

Autor wspomnianego na początku artykułu zaleca wklejanie paska trójkątów równobocznych w rozciętą wzdłuż równika kulistą bombkę, by zyskiwała tym sposobem talię, za którą można by ją wieszać na choince. Mnie jednak to się nie udawało – szklane bombki nie chciały współpracować, więc przyjrzałem się innym doskonałościom: wielościanom foremnym, zwanym też platońskimi.

Jeden z nich to wymieniony już ośmiościan foremny. Dzięki swoim symetriom ma on cztery talie, a nie jedną, jak większość antygraniastosłupów. Inne bryły foremne już antygraniastosłupami nie są. Ale śmiało uogólniając, możemy rozważyć 2-antygraniastosłup foremny: jego podstawy wyglądają jak odcinki, a różnią się od odcinków tym, że są ,,podwójne” – mają prawy bok i lewy bok. Jeśli zbudujemy taki 2-antygraniastosłup, to okaże się, że mamy czworościan foremny, i jest od razu (?) widoczne, że ma trzy talie opisane na kwadratach.

Za pomocą 5-antygraniastosłupa, narysowanego na górze strony, można jeszcze rozstrzygnąć problem talii dwudziestościanu foremnego – wystarczy na podstawach zafundować ,,czapeczki” – ostrosłupy z trójkątów równobocznych. Dwudziestościan będzie wtedy miał talię taką jak 5-antygraniastosłup (czyli opisaną na dziesięciokącie), ale nie jedną, tylko sześć.

Pozostałe dwa wielościany już tak prosto nie poddadzą się. W sprawie ich talii mamy jednak potężnego sojusznika – to Hugo Steinhaus. Rozwiązania można znaleźć w Kalejdoskopie matematycznym.

Kalejdoskop matematyczny Hugona Steinhausa został wydany w 1938 roku we Lwowie równocześnie z zamówioną przez Amerykanów angielską wersją (Mathematical snapshots). Ma wiele wydań w najrozmaitszych językach, w tym cztery polskie (,,najnowsze” wydanie, z 1989 roku, jest najsłabsze edytorsko – radzę poszukać wcześniejszych).
Przytoczony tu eksperyment jest w Kalejdoskopie oznaczony numerami 243–247, a w Delcie znalazł się w \(\Delta_{11}^{11}\) na stronie 0.

W Kalejdoskopie można znaleźć zachętę do takiego eksperymentu.

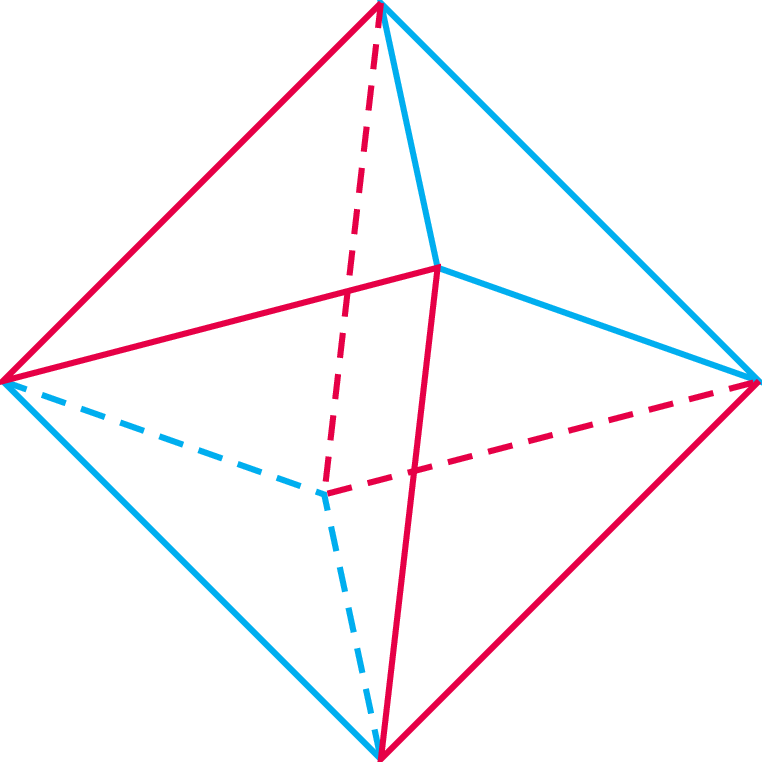
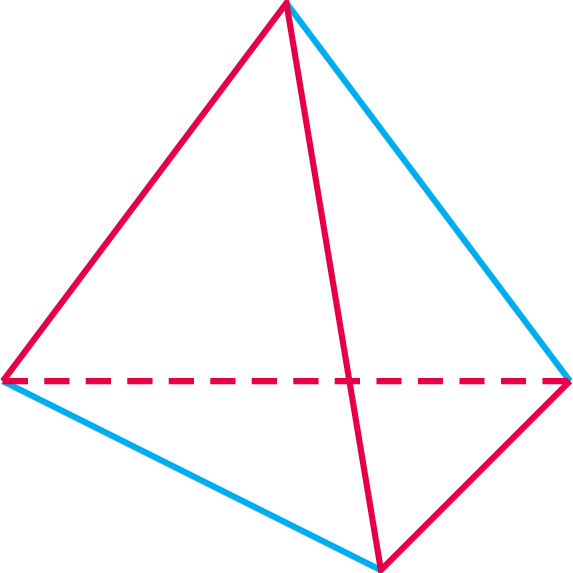
\(\bullet\) Z tekturki wytnij dwie takie figury, jak poniżej (bok 3 cm) i powyginaj wzdłuż przerywanych linii.

\(\bullet\) Połóż jedną na drugiej tak, by rogi dolnej jednakowo wystawały spod górnej.

\(\bullet\) Przyciskając środek palcem, nałóż recepturkę tak, by była nad rogami górnej i pod rogami dolnej.

\(\bullet\) PUŚĆ!

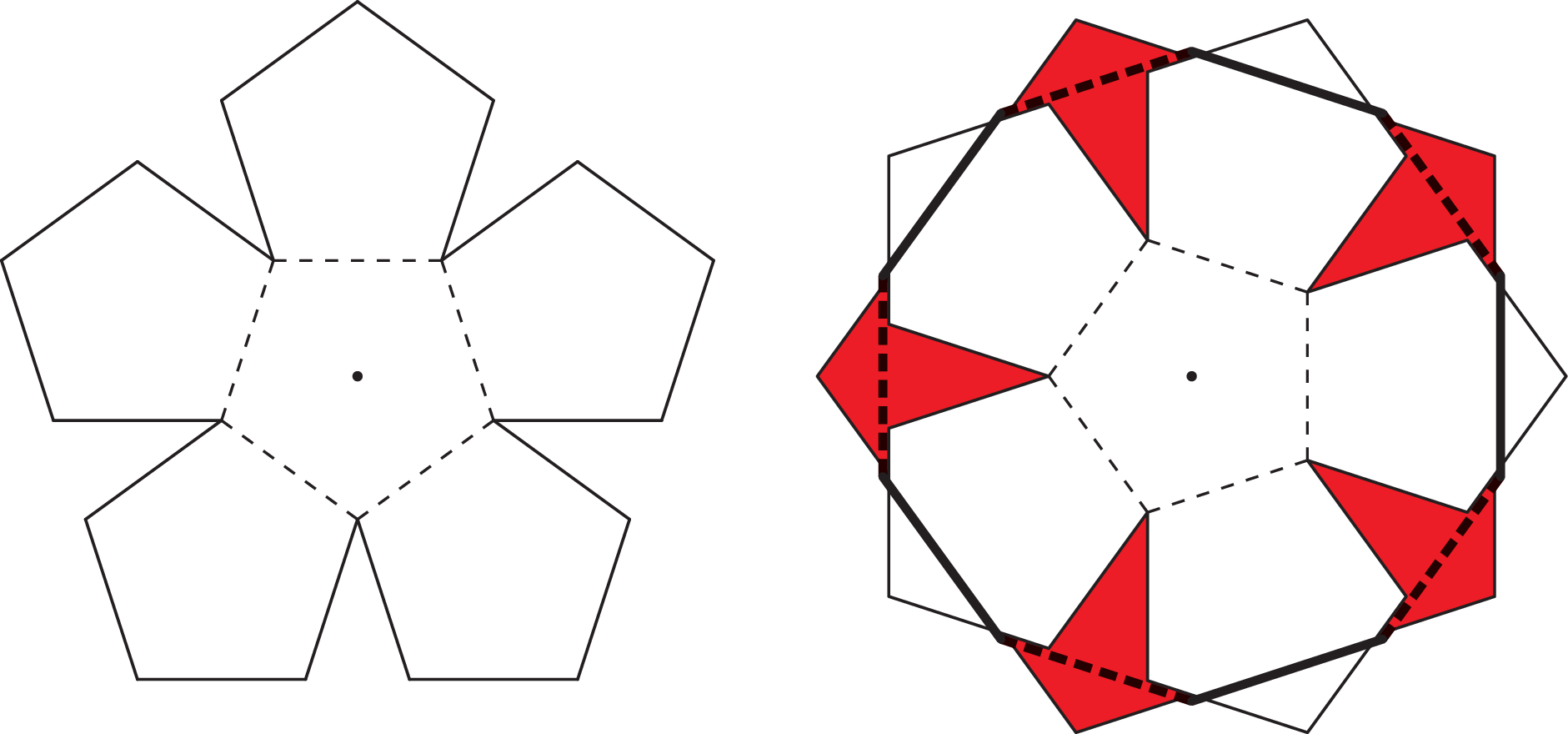
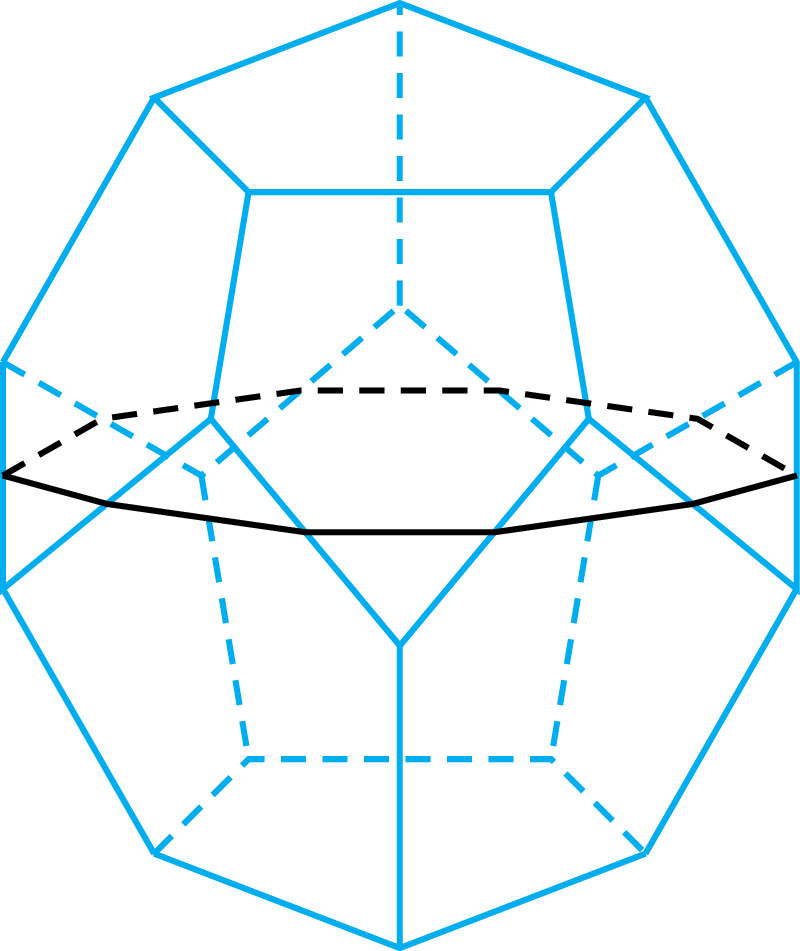
Wynik będzie mniej więcej taki, jak widać obok. Otrzymamy dwunastościan foremny (każdy zauważył, że tekturki składały się z pięciokątów foremnych). Można na to spojrzeć jak na modyfikację antygraniastosłupów: tym razem podstawy pięciokątne, jak trzeba, lekko obrócone, łączymy paskiem nie trójkątów równobocznych, lecz foremnych pięciokątów. Identyczna jak w przypadku antygraniastosłupów argumentacja wskazuje, że okrąg opisany na przecięciu płaszczyzną tak samo odległą od obu podstaw jest talią. Przecięcie to jest dziesięciokątem foremnym, o bokach będących połową przekątnej pięciokąta. Symetrie zaś dwunastościanu dowodzą, że takich talii jest sześć.

Studenci Autora omawianego artykułu wykonali całą serię prawdziwych, bo kartonowych, wielościanów wyposażonych w prawdziwe, bo miedziane, talie, a niemających związków z hiperboloidami.

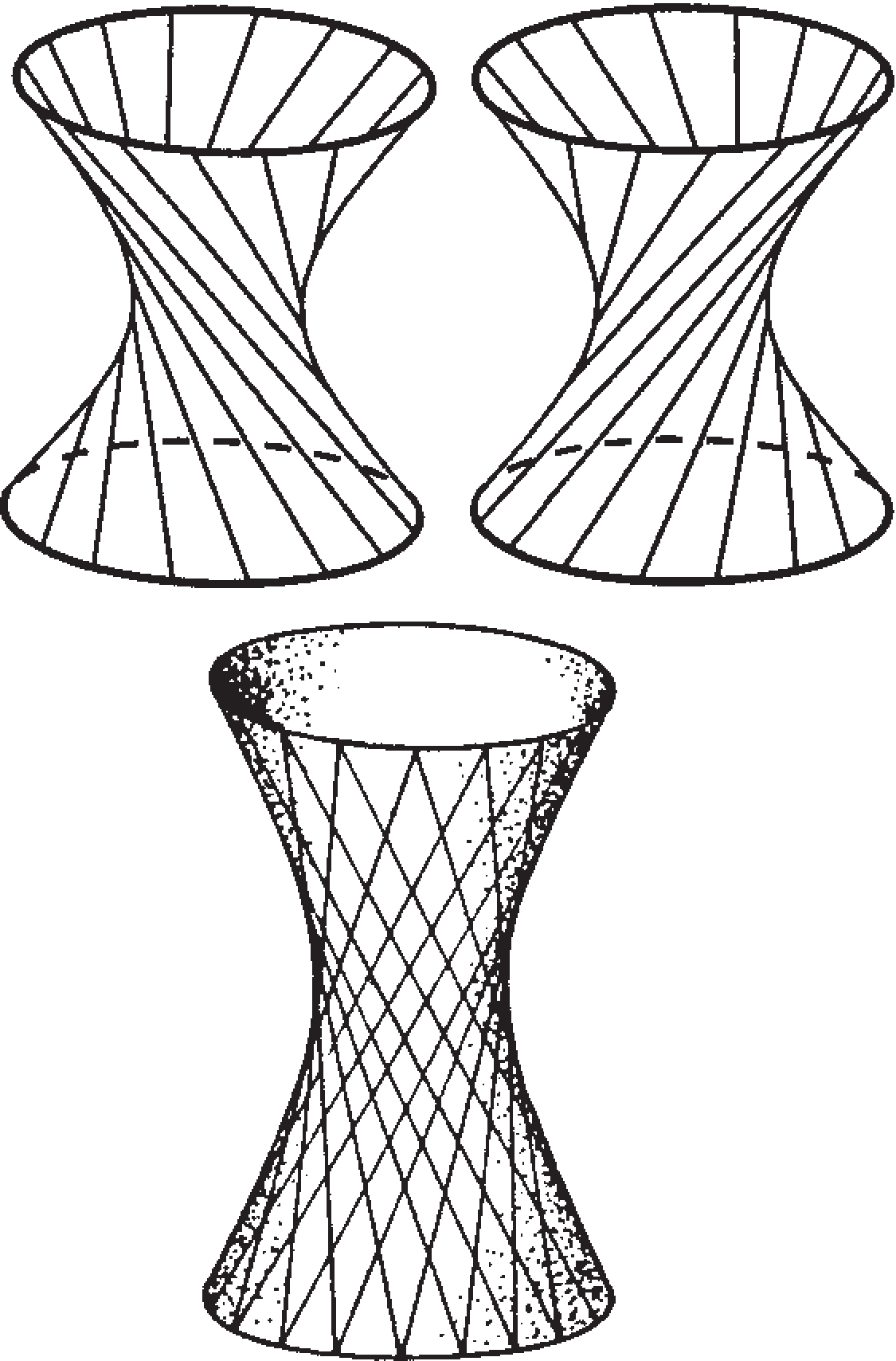
W Kalejdoskopie pod numerem (203) znajdujemy zdjęcie sześcianu obracającego się względem swojej dużej przekątnej. Widzimy tu dwie czapeczki (jak w dwudziestościanie) i fragment hiperboloidy obrotowej (jest ona wynikiem obracania prostej względem skośnej do niej osi). Tu słowo ,,talia” samo się narzuca – wręcz widoczny jest okrąg o promieniu będącym odległością obracanej prostej od osi obrotu (bo proste skośne mają jedną wspólną prostopadłą realizującą minimum odległości ich punktów).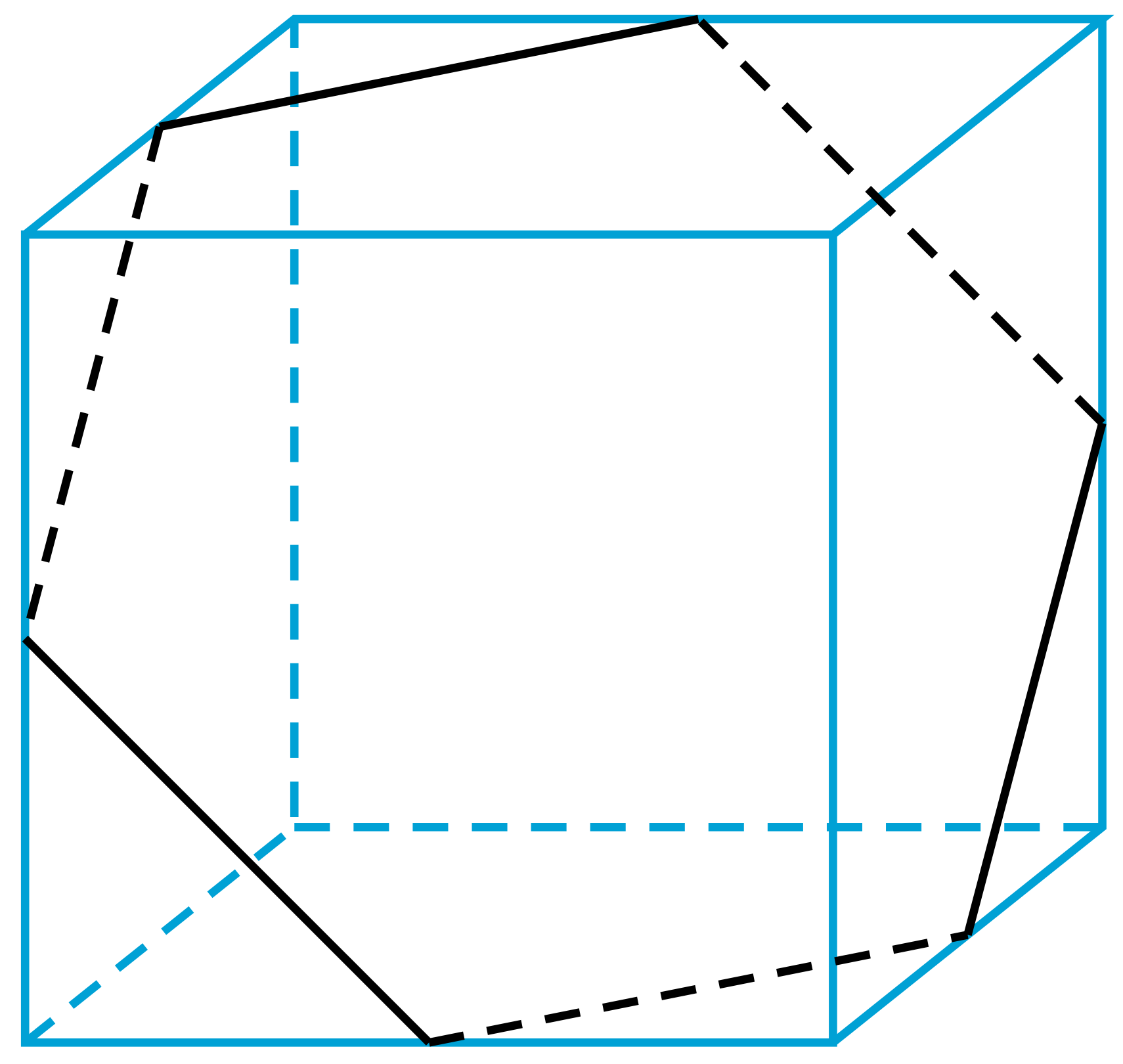

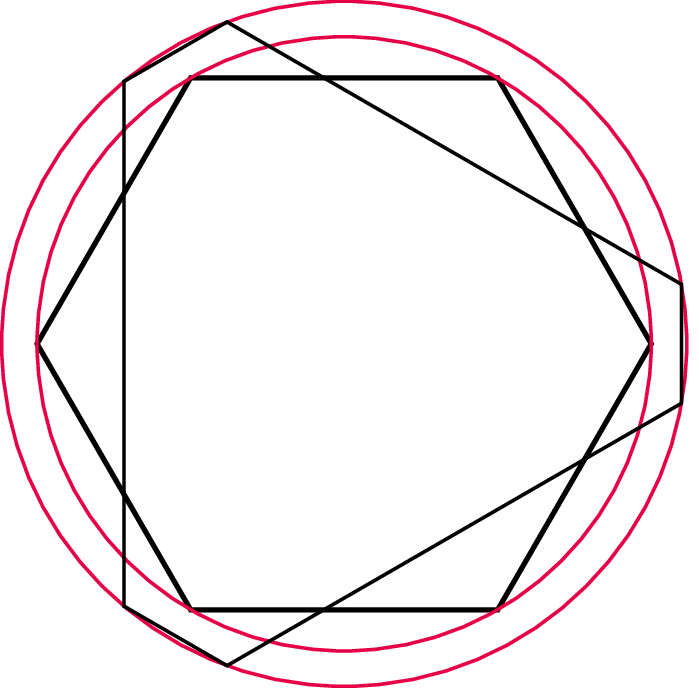
Powstanie tego zdjęcia udziela odpowiedzi na pytanie o talie sześcianu – da się go ,,wyjąć” z tego zdjęcia: talia sześcianu to okrąg opisany na jego przecięciu z płaszczyzną połowiącą prostopadle jego przekątną. To przecięcie to sześciokąt foremny o boku \({{\sqrt{2}}\over 2}.\) Talii jest tyle co przekątnych, czyli cztery.

Gdy spojrzymy na hiperboloidę w ten sposób, że powstaje ona z walca, którego podstawy są nieco względem siebie obrócone, to zobaczymy, że tworzące staną się skośne względem jego osi. A to demonstruje fakt, że konstrukcja hiperboloidy jest identyczna z konstrukcją antygraniastosłupa (tyle że jest ,,ciągła”). Co więcej, łatwo wskazać osie, podczas obrotu względem których każdy z występujących w tym tekście wielościanów może zafundować sobie taką fotkę, jaką Steinhaus zafundował sześcianowi – z kawałkiem hiperboloidy w środku.

I tak się okazało, że wszystkie przykłady talii wielościanów przytoczone w tym tekście to po prostu ukryta obrotowa hiperboloida jednopowłokowa.

Oczywiście istnieją wielościany wypukłe mające talię, a niespokrewnione z hiperboloidą, jak choćby ten z miedzianą talią widoczny na zdjęciu obok.