Afiliacja: Nauczyciel, Warszawa
Jak głosi legenda opowiadana o młodym Gaussie, pewnego dnia postawiono go przed zadaniem obliczenia sumy liczb naturalnych od 1 do 40 włącznie. Młodego Gaussa najwyraźniej mało co odrzucało bardziej niż perspektywa dodawania garstki całkiem niedużych liczb, więc zamiast tego, z użyciem pewnej chytrej sztuczki, wyprowadził ogólny wzór na \(n\)-tą liczbę trójkątną: \[T(n) = 1+2+3+ \dots + n.\] My także spróbujemy tego dokonać, ale wykorzystamy w tym celu interpretację kombinatoryczną podanej sumy. Następnie zaś przekonamy się, że nasza metoda pięknie się uogólnia i pozwala unikać dodawania nawet w wyraźnie trudniejszych sytuacjach.
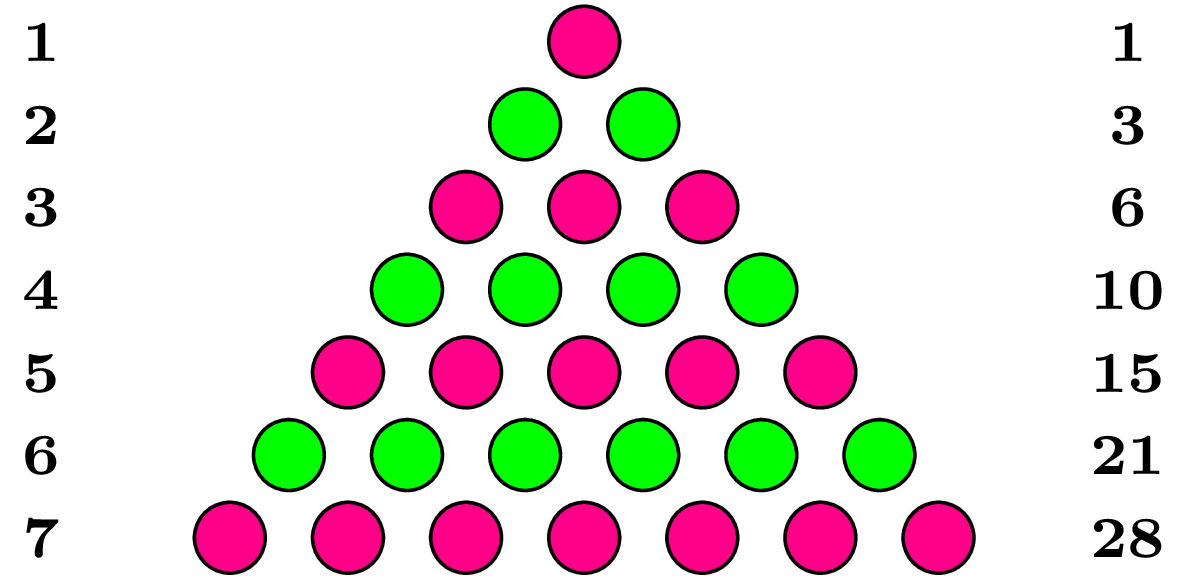
Liczby trójkątne
Wyobraźmy sobie przyjęcie dla fanów gier karcianych, na które oprócz gospodarza przybyło \(n\) gości. Na takim przyjęciu ktoś powinien zagrać w garibaldkę – grę dla dwóch osób. Na ile sposobów można wybrać dwójkę chętnych do tej gry?
Łatwo tę wartość obliczyć, uwzględniając kolejność przybywania gości. Kiedy na miejsce przybył pierwszy z nich, zastał jedynie gospodarza i mógłby co najwyżej zagrać z nim. Kiedy wszedł drugi, pojawiły się nowe opcje, bo teraz ten właśnie przybyły gość może zagrać z dowolną z dwóch już obecnych osób. Podobnie trzeci z przybyłych mógłby zagrać w parze z którąś z trzech obecnych osób. I tak dalej: dla \(k\)-tego gościa istnieje na tym przyjęciu dokładnie \(k\) dwójek, w których jest on ostatnim przybyłym członkiem. Zatem możliwych dwójek jest dokładnie \(1+2+3+ \dots + n.\) Innymi słowy, pogrupowaliśmy możliwe dwójki graczy według najpóźniej przybyłej osoby i okazało się, że ich łączna liczba jest \(n\)-tą liczbą trójkątną.
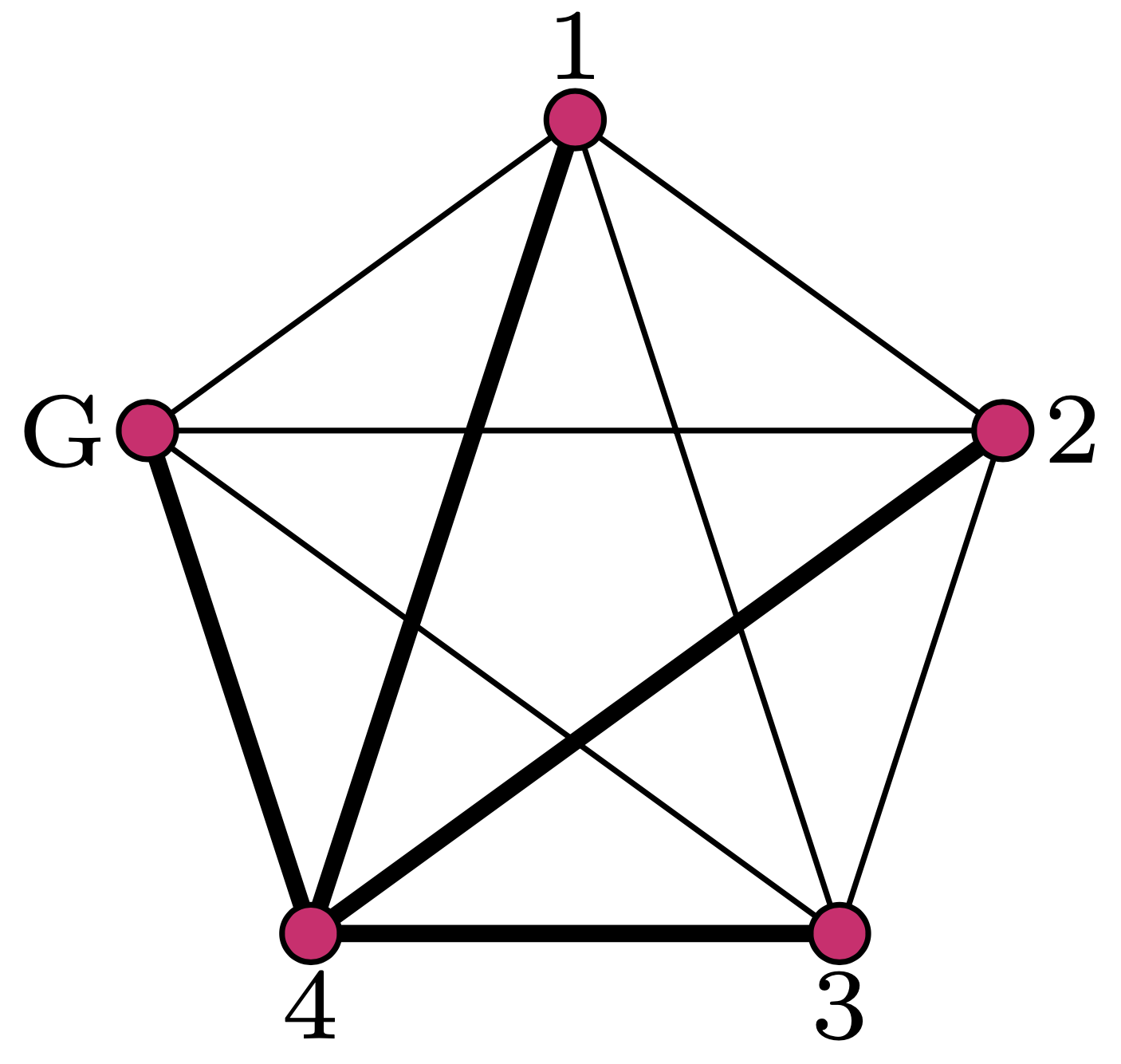
Można też to zagadnienie rozumieć jako zliczanie krawędzi w grafie pełnym
Z drugiej strony nie jest wcale trudno obliczyć ową liczbę bez takiego grupowania: przecież aby wybrać dwóch graczy, wystarczy wybrać jednego, dowolnego – to zrobimy na \(n+1\) sposobów – a następnie drugiego spośród pozostałych \(n.\) W ten sposób jednak policzylibyśmy każdą dwójkę dwukrotnie, bo każdy z dwóch jej członków mógł być wybrany jako ten pierwszy. Dochodzimy zatem do wniosku, że szukana liczba dwójek wynosi \(\frac{1}{2}n(n+1).\) Z całej tej opowieści wynika zaś tożsamość: \[T(n)=1+2+3+\dots+n=\frac{n(n+1)}{2}.\] Możemy teraz odpowiedzieć na pytanie Gaussa: sumą liczb naturalnych od 1 do 40 włącznie jest \(\frac{40\,\cdot\, 41}{2}=820.\)
Liczby piramidalne
Liczby piramidalne nazywa się też czworościennymi, gdyż typowa piramida ma 4, a nie 3, strony.
Zbadamy teraz dalsze możliwości zastosowanej powyżej metody. Obliczymy mianowicie \(n\)-tą liczbę piramidalną, równą sumie kolejnych liczb trójkątnych: \[P(n)=T(1)+T(2)+T(3)+\dots+T(n).\] Celowo nie podstawiamy tu żadnego wzoru za \(T(k),\) ponieważ będziemy chcieli korzystać przede wszystkim z opisanej powyżej interpretacji kombinatorycznej.
Wyobraźmy więc sobie przyjęcie dla fanów gier karcianych, na które oprócz dwojga gospodarzy przybyło \(n\) gości. Na takim przyjęciu ktoś powinien zagrać w preferansa – grę dla trzech osób. Na ile sposobów można wybrać taką trójkę graczy?
Podobnie jak ostatnio, rozważmy gości przyjęcia w kolejności ich przybywania, pamiętając o dwojgu obecnych przez cały czas gospodarzy. Gdy przybywa pierwszy gość, powstaje pierwsza możliwa trójka. W chwili przybycia drugiego pojawiają się nowe opcje, mianowicie te trójki, w których skład on wchodzi. Ogólnie, gdy przybywa \(k\)-ty gość, pojawia się pewna liczba nowych możliwości. Kluczowa obserwacja: trójek z udziałem właśnie przybyłego jest dokładnie tyle, co dwójek bez niego. Tych z kolei jest \(T(k),\) bo bez tego gościa dostępnych jest \(k+1\) osób (właśnie dlatego w tej opowieści mamy drugiego gospodarza). Wobec tego opisana liczba rzeczywiście jest równa \(T(1)+T(2)+T(3)+\dots+T(n),\) czyli \(P(n).\)
Znowu możemy jednak ominąć kolejność przybywania gości. Wystarczy zauważyć, że trójka graczy to jeden, wybrany spośród \(n+2,\) i jeszcze dwójka spośród \(n+1\) graczy, wybrana na \(T(n)\) sposobów. I znowu, uwzględniając, że w trójce dowolny gracz mógłby być tym pierwszym, otrzymujemy odpowiedź w nowej postaci: \(\frac{1}{3}(n+2)T(n).\) Po lekkim uporządkowaniu dochodzimy do tożsamości \[P(n)=T(1)+T(2)+T(3)+\dots+T(n)=\frac{n(n+1)(n+2)}{6}.\] W ten sposób możemy łatwo – i bez dodawania – obliczyć np. \(P(22),\) czyli sumę 22 początkowych liczb trójkątnych. Wynosi ona znaczące \[\frac{22\cdot 23\cdot 24}{6} = \textbf{2024}.\]
Dalej, wyżej!
Pokusimy się obecnie o daleko idące uogólnienie. Będziemy rozważać liczby trójkątne oraz piramidalne jako szczególne przypadki liczb piramidalnych pewnego wymiaru, równego tu odpowiednio 2 lub 3. Przyjmiemy, że liczba piramidalna danego wymiaru jest sumą początkowych liczb piramidalnych wymiaru o 1 niższego – można to interpretować jako układanie kulek w wielowymiarowe piramidalne stosy, tak jak dla liczb trójkątnych i piramidalnych.
Oznaczmy przez \(P_0(n)\) \(n\)-tą liczbę piramidalną wymiaru \(0\), umawiając się przy tym, że \(P_0(n)=1\) dla każdego \(n.\) Dalej, dla danego \(w>0\) niech \(P_w(n)= P_{w-1}(1)+P_{w-1}(2)+P_{w-1}(3)+\dots+P_{w-1}(n).\) Łatwo można zobaczyć, że wówczas \(P_1(n)=n,\) \(P_2(n)=T(n)\) oraz \(P_3(n)=P(n),\) czyli przyjęta przez nas konwencja rzeczywiście obejmuje wcześniejsze rozważania.
Jeśli, Drogi Czytelniku, przeżywasz tutaj małe déjà vu, to być może z powodu uderzająco podobnego zagadnienia, o którym pisał Wojciech Guzicki w \(\Delta^{7}_{95}\).
Czy możemy wyprowadzić ogólny wzór na \(P_w(n)\)? Okazuje się, że tak, a ponadto wystarczy powtórzyć rozumowanie przedstawione powyżej. Wyobraźmy sobie bowiem przyjęcie dla fanów gier karcianych, na którym obecnych jest \(w-1\) gospodarzy oraz \(n\) gości i chcemy. rozegrać partię \(w\)-ysiąca – gry dla \(w\) graczy.
Z jednej strony, gdy najwyższy numer gościa wśród grających wynosi \(k,\) to pozostałych możemy wybrać na \(P_{w-1}(k)\) sposobów. Rozpatrując kolejno możliwe \(k,\) dochodzimy do wniosku, że grających można wybrać na \({P_{w-1}(1)+P_{w-1}(2)+P_{w-1}(3)+\dots+P_{w-1}(n)},\) czyli \(P_w(n)\) sposobów.
Z drugiej strony natomiast można wybrać \(w\) graczy, wybierając najpierw jednego, a następnie pozostałych. Uwzględniając, że wśród \(n+w-1\) graczy można wybrać tego pierwszego na \(n+w-1\) sposobów, mamy nowy wzór na szukaną liczbę: \(\frac{n+w-1}{w} P_{w-1}(n).\) Podstawiając za \(P_{w-1}(n),\) a następnie za \(P_{w-2}(n)\) i tak dalej, dojdziemy do wzoru: \[P_{w}(n)=\frac{n(n+1)(n+2)\dots(n+w-1)}{1\cdot 2\cdot 3\cdot \ldots \cdot w},\] gdzie jedynkę w mianowniku dopisaliśmy głównie dla estetyki. Innymi słowy, jest to iloczyn \(w\) kolejnych liczb naturalnych, zaczynający się od \(n,\) podzielony przez iloczyn \(w\) kolejnych liczb naturalnych, ale tym razem zaczynając od 1. To nad wyraz elegancki wynik, nieprawdaż?
Czytelnik Edukowany, znający symbol Newtona i jego interpretację kombinatoryczną, może zaatakować rozpatrywany problem z jeszcze jednej strony. W ten sposób odkryje kombinatoryczny dowód wzoru \(\binom{n}{k}=\frac{n!}{k!(n-k)!}.\)
Pogłówkuj i Ty! Wyzwania
Oblicz, tj. przedstaw w postaci zwartego wzoru. Wszystkie chwyty są dozwolone!
1. \(n\cdot 1+(n-1)\cdot 2+(n-2)\cdot 3 + \dots + 1\cdot n.\)
2. \(n T(1) + (n-1) T(2) + (n-2) T(3) + \dots + 1\cdot T(n).\)
3. \(T(n)\cdot T(1) + T(n-1)\cdot T(2) + T(n-2)\cdot T(3) + \dots + T(1)\cdot T(n).\)
4. \(T(2n)-T(2n-1)+T(2n-2)-\dots+T(2)-T(1).\)
5. \(T(1)+T(3)+T(5)+\dots+T(2n-1).\)
Wskazówki do wyzwań
Jest pewne, że zaproponowane tu drogi do rozwiązań nie wyczerpują wszystkich możliwych pomysłów.
W zadaniach 1 – 3 można przepisać każdy z iloczynów \(k\cdot a\) jako sumę \(a+a+a+\dots+a,\) a następnie zmienić kolejność składników.
Można jednak zamiast tego odnieść się do interpretacji kombinatorycznej. Ustawmy w rzędzie \(n+2\) obecnych na przyjęciu, przy czym na początku stanie gospodarz, a za nim \(n+1\) gości. Pomyślmy teraz o gościu numer \(k\): spośród stojących przed nim można wybrać dwójkę na \(T(k)\) sposobów; spośród stojących za nim można wybrać jednego na \(n+1-k\) sposobów.
W zadaniu 4 z definicji wynika, że \(T(2k)-T(2k-1)=2k.\)
Zadanie 5 można rozwiązać, korzystając z 4, mianowicie dla \(A(n)=T(1)+T(3)+T(5)+\dots+T(2n-1)\) oraz \({B(n)=T(2)+T(4)+T(6)+\dots+T(2n)}\) znamy zarówno \(B+A,\) jak i \(B-A.\) Alternatywnie, z równości \({T(2n)=A(n)+B(n)}\) wynika, że \(A(n)=T(2n)-B(n),\) wystarczy więc obliczyć \(B(n).\) Można to uczynić dzięki tożsamości \(T(2k)=4T(k)-k,\) której udowodnienie pozostawiamy Czytelnikowi.
Nawiasem mówiąc, rozwiązując zadanie 5 dwoma sposobami, przez porównanie wyników otrzymujemy jeszcze jedną niebanalną tożsamość.
Odpowiedzi do wyzwań
1. \(P(n)\)
2. \(P_4(n)\)
3. \(P_5(n)\)
4. \(2T(n)\)
5. \(\frac{1}{2}P(2n)-T(n)\) albo \(T(2n)-4P(n)+T(n)\)