Afiliacja: Student, Wydział Fizyki Uniwersytetu Warszawskiego
Za jedno z większych osiągnięć współczesnej fizyki uznaje się Model Standardowy, który – mimo pewnych wad – pozwala przewidywać wyniki zderzeń wysokoenergetycznych cząstek z olbrzymią dokładnością. Od dziesiątek lat potwierdzają go eksperymenty we wszelkiej maści akceleratorach i detektorach, a w środowisku fizyków uchodzi za najlepszą teorię opisującą trzy z czterech fundamentalnych oddziaływań: elektromagnetyczne, słabe i silne.
O Modelu Standardowym i historii odkryć dokonywanych w akceleratorach pisał obszernie w siedmioodcinkowym cyklu Piotr Chankowski w \(\Delta^{1\ldots 6}_{16}\) oraz \(\Delta^2_{17}\). Jeden z odcinków cyklu (w \(\Delta^5_{16}\)) poświęcony był fizyce neutrin i ich oscylacjom.
Paweł Przewłocki pisał natomiast o detektorach neutrin w \(\Delta^{10}_{14}\), \(\Delta^3_{16}\).
O sukcesie Modelu Standardowego może świadczyć fakt, że w XXI wieku zaledwie dwa razy dokonano odkryć, które wymuszałyby jego modyfikację. Pierwsze dotyczyło oscylacji neutrin, drugie zaś cząstki Higgsa (znanej także jako boska cząstka). I choć to o tym drugim było zdecydowanie głośniej, to również oscylacje neutrin zasługują na szersze poznanie.
Czym są neutrina?
W bardzo wielkim skrócie można je nazwać nieśmiałymi, unikającymi poklasku braćmi naładowanych leptonów. Neutrina, pozbawione ładunku elektrycznego, oddziałują tylko słabo. Oddziaływania słabe należą zaś do najtrudniejszych do zaobserwowania w przyrodzie, ponieważ ich zasięg jest około tysiąc razy mniejszy niż promień protonu. Tak blisko neutrina trzeba się znaleźć, by poczuć jego oddziaływanie.
Z tego powodu wykrywamy neutrina o wiele rzadziej niż pozostałe cząstki elementarne. I tak jak padający na Ziemię strumień światła rozproszy się lub zostanie pochłonięty, tak strumień neutrin w znacznej części przeleci między atomami Ziemi – prawie niewykrywalny.
W przyrodzie istnieją trzy rodzaje neutrin, z których każde przenosi inny rodzaj ,,zapachu”. Nie ma on, rzecz jasna, nic wspólnego z jego fizycznym zapachem, a samego neutrina oczywiście nie da się powąchać – po prostu fizycy cząstek bardzo lubią przenosić na świat kwantowy nazwy z życia codziennego.
Zapach neutrin wiąże się z pewnymi zasadami zachowania, które łączą je z pozostałą trójką leptonów. I tak neutrino elektronowe ma ten sam zapach co elektron, neutrino mionowe taki sam jak mion, a neutrino taonowe jak taon. Istotą zapachu jest fakt, że – tak jak np. ładunek elektromagnetyczny – jego ilość w każdym procesie musi być zachowana. Innymi słowy zapach nie może znikać ani pojawiać się znikąd.
Jako ilustrację tej zasady możemy wykorzystać rozpad \(\beta ^+,\) w którym następuje przemiana protonu w neutron. Gdybyśmy nie dodali do niego kolejnych produktów, niezachowany byłby ładunek elektromagnetyczny. I rzeczywiście w wyniku rozpadu \(\beta ^+\) otrzymuje się także pozyton (czyli anty-elektron), oznaczany jako \(e^+.\) On z kolei niesie zapach ,,anty-elektronowy”, do którego zrównoważenia potrzebujemy cząstki o zapachu elektronowym – zatem kolejnym produktem rozpadu okazuje się neutrino elektronowe, oznaczane jako \(\nu_e.\)
Efektywnie obserwujemy więc rozpad: \[p \rightarrow n + e^+ + \nu_e,\] w którym zachowany jest zarówno ładunek elektromagnetyczny, jak i zapach elektronowy.
Jakie znaczenie ma rozpad beta?
Jest niezwykle istotny dla reakcji jądrowych w Słońcu. Na przykład w dominującym cyklu wodorowym następuje fuzja dwóch wodorów w deuter, który wymaga właśnie przemiany protonu na neutron. Ciągłe rozpady beta czynią ze Słońca wielką fabrykę neutrin elektronowych, które bezproblemowo uciekają z jądra i rozlatują się we wszystkich kierunkach. W tym na Ziemię, gdzie możemy je mierzyć.
Jedną z pierwszych takich prób podjęto w latach siedemdziesiątych w eksperymencie Homestake. Neutrina słoneczne uderzały w zgromadzony w zbiornikach chlor, zamieniając go w argon, który następnie wychwytywano i zliczano.
Ponieważ neutrina są cząstkami słabo oddziałującymi, eksperyment wymagał szczególnych przygotowań. Zgromadzono trzysta osiemdziesiąt tysięcy litrów zawierającego chlor tetrachloroetenu i umieszczono w kopalni, półtora kilometra pod poziomem morza – aby odizolować układ od otoczenia i pozbyć się wszelkich szumów. Neutrina elektronowe, uderzając w chlor, wywoływały reakcję, której produktem był zliczany później argon: \[\nu_e + \ce{^{37}Cl} \rightarrow \ce{^{37}Ar^+} + e^-.\] W ten sposób otrzymano liczbę uderzeń neutrin w zbiorniki, skąd oszacowano strumień neutrin. Problem leżał w tym, że rezultat nie zgadzał się z dotychczasowymi przewidywaniami teoretycznymi – konkretnie brakowało około dwóch trzecich neutrin słonecznych. Rezultat potwierdziły kolejne detektory, na czele z Super-Kamiokande i obserwatorium Sudbury.
Oznaczało to, że coś było nie tak z teorią. A po początkowych próbach modyfikacji teorii działania Słońca fizycy zaczęli skłaniać się ku hipotezie, że brakujące neutrina ,,gubią się” w drodze ze Słońca.
Mechanizm wyjaśniający zagadkę zaproponował już w 1957 roku Bruno Pontecorvo, opierając się na analogicznym procesie zachodzącym wśród kwarków (znanym jako mieszanie kwarków i opisywanym przez macierz CKM). Rozwiązanie Pontecorvo nazywamy dziś oscylacjami neutrin.
Czym jest macierz CKM i mieszanie kwarków, objaśniał Piotr Chankowski w \(\Delta_{16}^{1}\)
Czym są oscylacje neutrin?
Żeby oscylacje mogły zachodzić, muszą być spełnione pewne warunki. Po pierwsze masy neutrin muszą się od siebie różnić – mówimy, że neutrina występują w trzech możliwych stanach masowych. Po drugie (i to jest właśnie kluczowe dla mieszania) relacja między zapachem a masą nie może być tak jednoznaczna, jak w przypadku naładowanych leptonów. Istotą pomysłu jest stwierdzenie, że neutrino, które obserwujemy jako cząstkę o ściśle określonym zapachu (np. neutrino elektronowe), nie ma dobrze określonej masy. W języku mechaniki kwantowej mówimy, że jest superpozycją trzech stanów masowych. Analogicznie, cząstka o ściśle określonej masie jest superpozycją trzech różnych stanów zapachowych. Inaczej mówiąc, neutrino elektronowe (określony zapach) nie jest tym samym co neutrino najlżejsze, bo ma niewielkie domieszki stanów o wyższych masach. Natomiast neutrino najlżejsze oprócz głównego wkładu od neutrina elektronowego niesie w sobie dodatkowo niewielkie wkłady od stanu mionowego i taonowego.
Naładowane leptony występują w trzech zapachach: elektron, mion i taon. Naładowany lepton o określonym zapachu ma określoną masę: elektron jest najlżejszy, a taon najcięższy. Nie ma tu żadnego mieszania ani oscylacji.
Mieszanie można wyobrażać sobie geometrycznie w przestrzeni trójwymiarowej w następujący sposób. Trzy stany masowe reprezentujemy jako trzy parami prostopadłe wektory unormowane (czyli o długości równej jeden). Analogicznie definiujemy trójkę wektorów opisujących stany zapachowe. Mamy więc dwie tzw. bazy ortonormalne w tej samej przestrzeni. W przypadku naładowanych leptonów obie trójki (bazy ortonormalne) się pokrywają. W przypadku neutrin te dwie trójki wektorów są względem siebie trochę obrócone. Sytuację dodatkowo ubogaca fakt, że wszystko to dzieje się w przestrzeni trójwymiarowej, ale zespolonej, a nie rzeczywistej. Dlatego oprócz trzech kątów pojawia się jeszcze dodatkowa zespolona faza.
Zwyczajowo stany masowe oznaczamy \(\ket{\nu_1}, \ket{\nu_2}\) i \(\ket{\nu_3},\) a stany zapachowe \(\ket{\nu_e}, \ket{\nu_\mu}\) i \(\ket{\nu_\tau}.\) Te dwie trójki stanów możemy wyobrażać sobie jako trójki wektorów w trójwymiarowej przestrzeni (patrz margines). Mieszanie, które możemy interpretować jako coś w rodzaju obrotu, opisujemy przez kąty mieszania. Dla uproszczenia rozważymy najpierw przykład dwóch neutrin zamiast trzech. Wówczas mieszanie opisywalibyśmy jako obrót na płaszczyźnie w następujący sposób: \[\begin{cases} \ket{\nu_e} = \cos{\theta} \ket{\nu_1} + \sin{\theta} \ket{\nu_2}\\ \ket{\nu_\mu} = -\sin{\theta} \ket{\nu_1} + \cos{\theta} \ket{\nu_2}. \end{cases}\] W tym przypadku \(\theta\) oznacza właśnie kąt mieszania. Gdy rozszerzymy teorię do trzech neutrin, pojawią się trzy kąty mieszania (\(\theta_{12}, \theta_{13}, \theta_{23}\)) i dodatkowo jedna faza zespolona \(\delta,\) która ma znaczenie przy transmisji przez ośrodek materialny.
Po emisji ze Słońca neutrina poruszają się (już w stanach masowych) w przestrzeni kosmicznej z prędkością bliską prędkości światła i energią \(E\) o wiele większą niż ich masa spoczynkowa. Wówczas możemy opisać ich propagację wzorem: \[\ket{\nu_i (L)} = \ket{\nu_i (0)} e^{-iL(E+\frac{m_i^2}{2E})},\] który mówi tyle, że każdy ze stanów masowych porusza się jak fala o długości proporcjonalnej do odwrotności \(\big(E+\frac{m_i^2}{2E}\big).\) Kluczowe jest to, że długość ta (czyli również częstość fali) jest inna dla każdej masy.
Na koniec zaś dokonujemy pomiaru neutrin, które dolecą do Ziemi. Ponieważ każdy ze stanów masowych porusza się jako fala o innej długości, więc fale, które w chwili emisji były w tej samej fazie, docierają do Ziemi przesunięte względem siebie. W konsekwencji ich złożenie reprezentuje inny stan niż stan początkowy wyemitowany na Słońcu. To powoduje – nawet jeśli stan początkowy był stanem o ustalonym zapachu – że stan końcowy może być już złożeniem stanów o różnych zapachach. Po dokonaniu kilku przekształceń algebraicznych odzwierciedlających te zmiany otrzymujemy prawdopodobieństwo zmiany zapachu \(e\) w zapach \(\mu\) (dla przypadku dwóch neutrin): \[P_{e \rightarrow \mu} = \sin^2 2\theta \sin^2\left(\frac{(m_2^2 - m_1^2)L}{4E}\right),\] gdzie \(L\) to przebyta odległość od źródła, \(E\) to energia wyemitowanego neutrina, natomiast \(m_1\) i \(m_2\) to dobrze określone masy neutrin \(1, 2.\) Oczywiście mamy też: \[P_{e \rightarrow e} = 1 - \sin^2 2\theta \sin^2\left(\frac{(m_2^2 - m_1^2)L}{4E}\right).\] Jak w praktyce (w przypadku trzech neutrin) działają oscylacje neutrin, można zobaczyć na wykresie.
Obliczenie prawdopodobieństwa zmiany zapachu wymaga uwzględnienia dwukrotnej zmiany bazy (z zapachowej na masową przy emisji neutrin i w drugą stronę przy ich detekcji) oraz dokonaniu kilku przekształceń algebraicznych. W skrócie: neutrino emitowane ma określony zapach, np. elektronowy, czyli składowe w kierunku zapachu mionowego i taonowego są równe zero. Rozkładamy ten stan w bazie masowej – tu wszystkie składowe będą niezerowe. Każda z tych składowych ewoluuje niezależnie (poruszają się jako fala o innej długości), pokonując tę samą odległość, co matematycznie sprowadza się do tego, że każda składowa pomnoży się przez inną liczbę zespoloną o module jeden. Na koniec te trzy stany masowe, które doleciały do Ziemi, sumujemy. Ponieważ współczynniki przy stanach masowych zmieniły się w różny sposób, suma ta nie musi być równa wyjściowej sumie. Oznacza to, że stan cząstki ulegnie zmianie. Gdy rozłożymy go teraz w bazie zapachowej, to okaże się, że składowe w kierunku każdego ze stanów zapachowych będą na ogół różne od zera.
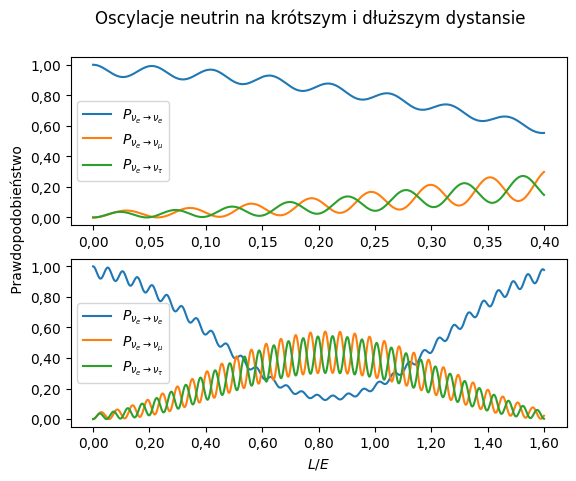
Co mówią nam oscylacje?
Z powyższych wzorów wynika, że niektóre neutrina, powstałe na Słońcu jako neutrina elektronowe, z niezerowym prawdopodobieństwem będziemy wykrywali jako neutrina mionowe (lub taonowe). O ile \(L \neq 2k\pi,\) to \(P_{e \rightarrow \mu} > 0.\) Przynosi to rozwiązanie zagadki neutrin słonecznych, które w istocie nie znikają w tajemniczych okolicznościach, tylko zmieniają swój zapach, a nasze detektory są czułe tylko na neutrina elektronowe.
Nie jest to jednak ani jedyny, ani najważniejszy wniosek. Warto zauważyć, że wzór na oscylacje zawiera pod sinusem różnicę kwadratów mas neutrin. Oznacza to, że przynajmniej dwa z nich (a najprawdopodobniej wszystkie) muszą mieć niezerową masę! Fakt ten stanowił spore wyzwanie dla Modelu Standardowego, bowiem wcześniej zakładano, że neutrina jak fotony są cząstkami bezmasowymi. Odkrycie oscylacji zmusiło fizyków cząstek do przeformułowania swojej największej teorii, dodania dodatkowych elementów – kątów mieszania oraz mas – i zadania sobie kolejnych pytań, na przykład o źródło mas neutrin.
Odkrycie było na tyle ważne, iż poświęcono mu aż dwie nagrody Nobla: w 2002 i 2015 roku. Otrzymały je osoby odpowiedzialne za budowę detektorów (Homestake, Sadbury i Super-K); najpierw Raymond Davis i Masatoshi Koshiba, a następnie Takaaki Najita i Arthur McDonald.
Stoi ono również u podstaw rozwoju całej gałęzi badań nad neutrinami i fizyką zapachów. Fizycy teoretyczni wciąż zadają sobie pytania, skąd biorą się takie kąty mieszania, a także zastanawiają się nad naturą neutrin i spekulują o ich masywniejszych partnerach (znanych jako sterylne neutrina). Pytania o tyle interesujące, że z racji ich skrytej natury nasza wiedza na temat neutrin jest skromniejsza, niż byśmy chcieli.
Symetria P oznacza odbicie lustrzane, a symetria C to zamiana wszystkich cząstek na antycząstki. Badanie zachowania symetrii CP oznacza sprawdzanie, czy Wszechświat odbity w lustrze, w którym wszystkie cząstki zamienimy na antycząstki, będzie miał dokładnie takie same własności jak nasz. Fizycy teoretyczni poszukują łamania symetrii CP między innymi w celu wyjaśnienia, dlaczego we Wszechświecie istnieje więcej materii niż antymaterii.
Fizycy doświadczalni nie ustają zaś w planowaniu kolejnych eksperymentów mających zgłębić nieodkryte dotychczas tajemnice tych nieuchwytnych cząstek. Badają, jak neutrina rozpraszają się w atmosferze, czy zachowują symetrię CP, a także wyznaczają coraz dokładniej kąty mieszania. Poza neutrinami słonecznymi badają również te produkowane w akceleratorach – a jest to o tyle wygodne, że znając zakres energii zderzeń, możemy dokładnie określić, gdzie najlepiej postawić detektor neutrin, jeśli chcemy na przykład zwiększyć prawdopodobieństwo oscylacji. W planach są również kolejne wielkie detektory, w tym Hiperkamiokande i DUNE, które – miejmy nadzieję – umożliwią nam kolejne wielkie odkrycia.
