Errata do wersji w druku: Zdanie "Przypomnijmy, że \(\phi = \frac{\sqrt{5}+1}{2}\) jest dodatnim rozwiązaniem." należy skrócić do "Przypomnijmy, że \(\phi = \frac{\sqrt{5}+1}{2}.\)"
Za błąd wprowadzony przez redakcję przepraszamy.
Afiliacja: CWI, Amsterdam i Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Konstrukcja pięciokąta foremnego jest omówiona w Elementach Euklidesa i stanowi zwieńczenie szeregu wcześniej występujących w tym dziele rezultatów. Robin Hartshorne, autor książki, która jest swego rodzaju przewodnikiem po Elementach, napisał: ,,Jeśli istnieje coś takiego jak piękno w dowodzie matematycznym, to wierzę, że dowód Euklidesa poprawności konstrukcji pięciokąta foremnego tworzy standard pięknego dowodu”.
R. Hartshorne, Geometry: Euclid and Beyond, Springer, str. 50, 2000.
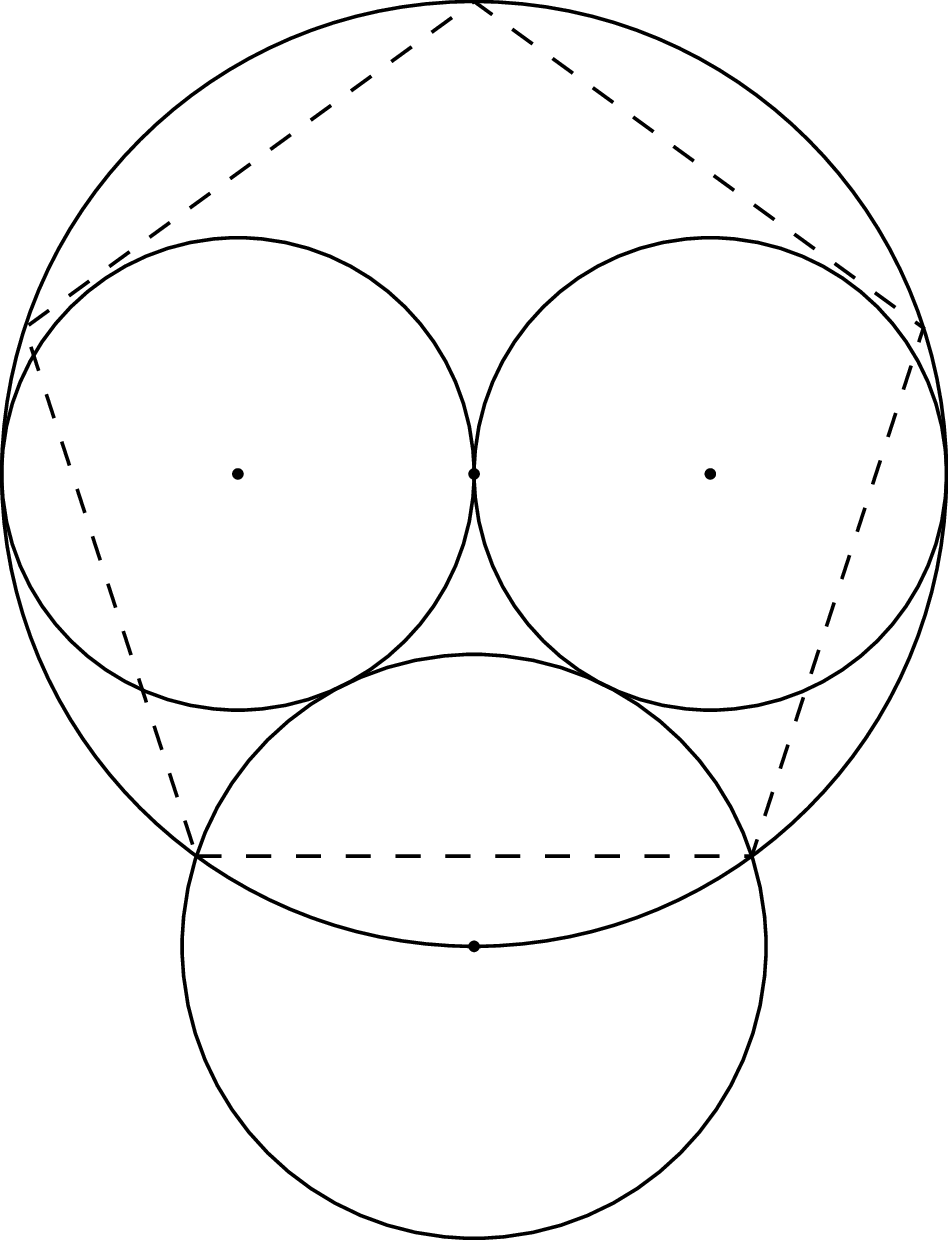
Rys. 1. Konstrukcja pięciokąta foremnego według Y. Hirano. Zaznaczone punkty to środki odpowiednich okręgów
Celem tej notki jest przedstawienie eleganckiej i szczególnie prostej konstrukcji pięciokąta foremnego, przypisywanej japońskiemu matematykowi z XIX wieku, Yosifusie Hirano (zobacz: A. Bogomolny, http://www.cut-the-knot.org/, Regular pentagon construction by Y. Hirano, 2014). Konstrukcja ta opiera się na następującym prostym rysunku (rys. 1).
Najpierw rysujemy okrąg. Następnie wewnątrz niego rysujemy dwa okręgi, każdy dwa razy mniejszy, tak aby stykały się one ze sobą i z pierwotnym okręgiem (wtedy środki małych okręgów leżą na średnicy dużego). Na koniec rysujemy czwarty okrąg tak, aby był styczny do mniejszych okręgów, a jego środek znajdował się w punkcie przecięcia pierwotnego okręgu z jego średnicą prostopadłą do średnicy przecinającej środki mniejszych okręgów. Wówczas punkty przecięcia pierwotnego i ostatniego okręgu określają bok pięciokąta foremnego wpisanego w pierwszy okrąg.
Rys. 2. Złoty trójkąt
Twierdzenie o złotym trójkącie można prościej udowodnić, korzystając z obserwacji, że w pięciokącie foremnym z bokami o długości \(a\) i przekątnymi o długości \(b\) zachodzi \(\frac{b}{a} = \phi,\) którą to równość udowodniliśmy w naszym artykule Elegancki dowód twierdzenia Ptolemeusza w \(\Delta^{8}_{24}\).
Aby udowodnić poprawność tej konstrukcji, rozważamy najpierw trójkąt równoramienny, w którym długość boku \(b\) jest w złotej proporcji \(\phi\) do podstawy \(a\) (rys. 2). Taki trójkąt nazywany jest złotym trójkątem. Pokażemy, że jego kąty wynoszą \(36^{\circ},\) \(72^{\circ}\) i \(72^{\circ}.\)
W tym celu zaznaczmy odległość \(a\) na jednym z pozostałych boków trójkąta, połączmy uzyskany punkt z przeciwległym wierzchołkiem i nadajmy nowej linii oraz odpowiednim kątom nazwy jak na rysunku. Z założenia \(\frac{b}{a} = \phi.\) Przypomnijmy, że \(\phi = \frac{\sqrt{5}+1}{2}.\) Czyli \(\phi\) spełnia równanie \(\phi^2 - \phi = 1\) lub \(\phi = \frac{1}{\phi - 1},\) a więc \[\frac{b}{a} = \frac{1}{{\frac{b}{a} - 1}} = \frac{a}{b-a} = \frac{a}{c}.\]
Rozważmy teraz pierwotny trójkąt równoramienny i trójkąt utworzony przez boki \(a, d, c.\) Współdzielą one kąt \(\gamma,\) a właśnie pokazaliśmy, że w obu trójkątach boki tworzące \(\gamma\) mają ten sam stosunek (dla pierwotnego trójkąta zachodzi bowiem \(b = a+c\)). A więc te trójkąty są podobne, stąd \(a = d\) i \(\beta = \delta.\)
Wynika stąd, że trójkąt o bokach \(b, d, a\) jest również równoramienny. Stąd \(\alpha = \beta,\) czyli kąty \(\alpha, \beta\) i \(\delta\) są równe. Ponadto \(\alpha + \delta = \gamma,\) zatem \(\alpha + \beta + \gamma + \delta = 2 \alpha + \beta + 2 \delta = 5 \beta.\) Ale \(\alpha + \beta + \gamma + \delta = 180^{\circ},\) więc \(\beta = 36^{\circ}\) i \(\alpha + \delta = \gamma = 72^{\circ}.\)
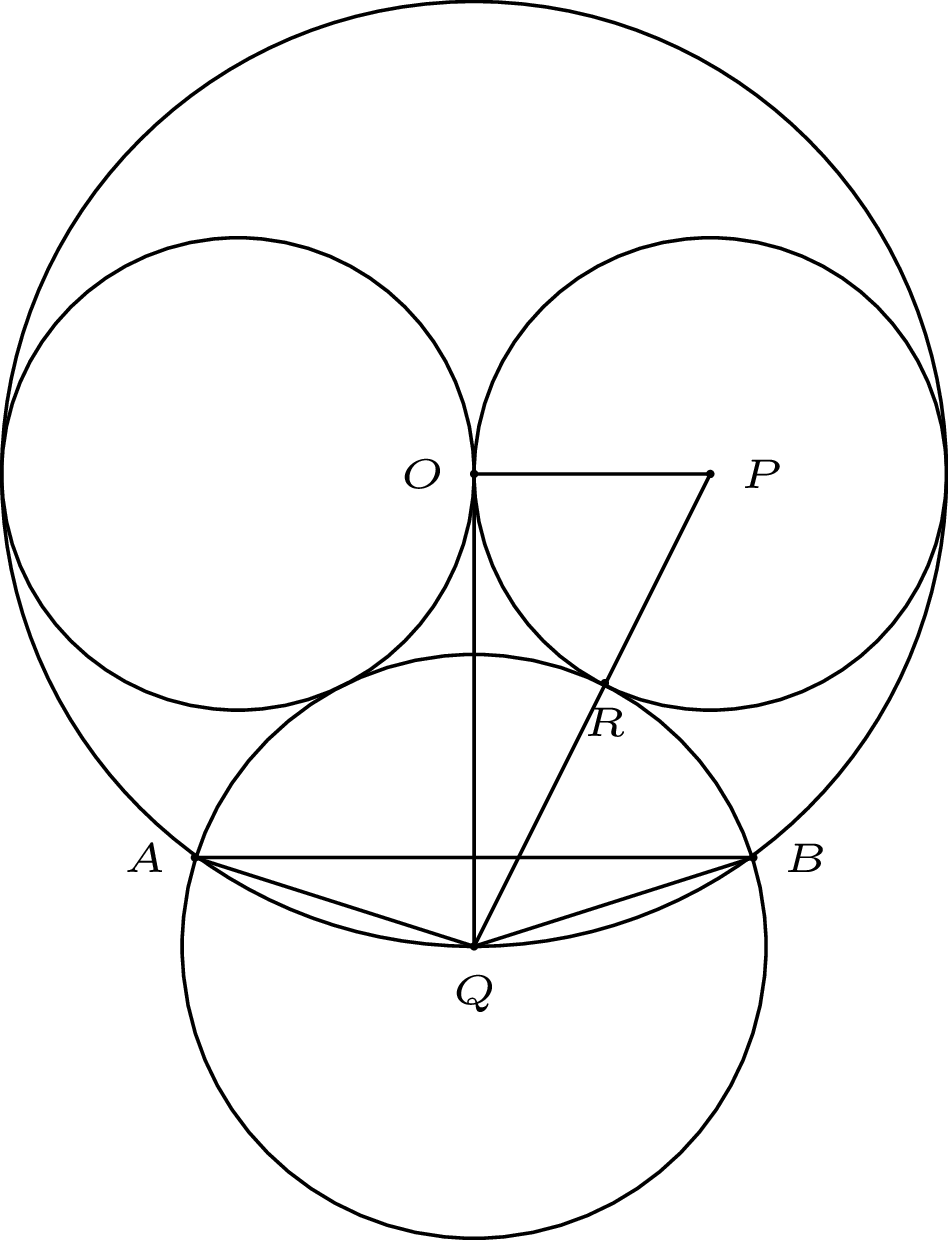
Rozważmy teraz rysunek 3, gdzie \(R\) jest punktem styczności czwartego okręgu z prawym okręgiem.
Rys. 3. Analiza konstrukcji Hirano
Załóżmy, że \(OQ = 1.\) Wówczas \(PO = PR = \frac12,\) a więc z twierdzenia Pitagorasa \(PQ = \sqrt{PO^2 + OQ^2} = \frac{\sqrt{5}}{2}.\) Stąd \(QB = QR = PQ - PR = \frac{\sqrt{5}-1}{2}.\) Oznacza to, że w trójkącie równoramiennym \(OQB\) mamy: \[\frac{OQ}{QB} = \frac{2}{\sqrt{5}-1} = \frac{2 (\sqrt{5}+1)}{(\sqrt{5}-1) (\sqrt{5}+1)} = \frac{\sqrt{5}+1}{2} = \phi,\] czyli \(OQB\) jest złotym trójkątem. Z powyższej analizy złotego trójkąta mamy \(\measuredangle QOB = 36^{\circ}.\) Z symetrii \(\measuredangle QOA = 36^{\circ},\) więc \(\measuredangle AOB = 72^{\circ}.\) To pokazuje, że \(AB\) jest bokiem pięciokąta foremnego wpisanego w pierwotny okrąg.
Tekst oparty na załączniku 13 z książki: Krzysztof R. Apt, ,,A Brief History of Mathematics for Curious Minds”, World Scientific, 2024.