Afiliacja: Uczennica, XIV LO im. Stanisława Staszica w Warszawie;
Doktorant, Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Niektóre zagadnienia z dziedziny informatyki dają się rozwiązać za pomocą algorytmów symulujących określone procesy. Dostajemy w ten sposób poprawne odpowiedzi, ale złożoność programu zależy od stopnia skomplikowania symulacji. Jeśli czas działania programu nie jest dla nas satysfakcjonujący (na przykład dla dużych danych wejściowych), to szukamy rozwiązania bardziej eleganckiego, choćby dla pewnych szczególnych przypadków. W tym artykule skupimy się na tego typu problemie, pojawił się on już w Delcie cztery lata temu, w artykule ,,Raz, dwa, trzy, wychodź ty!” Piotra Zarzyckiego i został przedstawiony od strony matematycznej. Tym razem skupimy się na jego informatycznym aspekcie.
Ostatnia osoba przy stole
W 2012 roku na Przedmiotowym Konkursie Informatycznym LOGIA pojawiło się następujące zadanie:
Przy okrągłym stole \(n\) uczestników spotkania siedzi na krzesłach ponumerowanych od \(1\) do \(n.\) Kolejno co \(k\)-ta osoba wstaje i opuszcza spotkanie. Zadaniem Antka jest wskazanie osoby, która pozostanie przy stole jako ostatnia.
Naszym celem jest więc napisanie funkcji, która jako wejście przyjmuje liczby \(n\) i \(k,\) a zwraca numer krzesła, które zostanie opuszczone jako ostatnie. Jest to znane zadanie kombinatoryczne nazywane problemem Józefa Flawiusza.
Uczestnicy konkursu mogli rozwiązać to zadanie na kilka sposobów;
standardowe podejście to wykorzystanie symulacji wypraszania kolejnych osób ze
spotkania, co można zapisać następująco (w poniższym algorytmie przyjmujemy, że listę indeksujemy od \(0\)):
W tym podejściu przechowujemy numery osób na liście, którą w kolejnych krokach
skracamy, co odpowiada wypraszaniu kolejnych osób. Takie rozwiązanie, działające w złożoności czasowej \(\mathcal O(n^2)\) (pojedyncze usunięcie elementu z listy ma pesymistyczną złożoność \(\mathcal O(n)\)), wystarczało do uzyskania maksymalnej liczby punktów.
Rozwiązanie to można nieco poprawić, uzyskując złożoność \(\mathcal O(nk)\) – zamiast usuwać elementy ze środka listy, przenosimy \(k - 1\) początkowych elementów listy na jej koniec, a potem usuwamy element, który aktualnie znajduje się na początku.
Warto się jednak zastanowić, czy zadania nie można rozwiązać zupełnie
inaczej. Idealnie byłoby, gdyby istniał taki wzór na pozycję ostatniej osoby,
który można wyliczyć za pomocą prostych operacji arytmetycznych.
Okazuje się, że nie jest to takie proste. Dla \(k=2\)
istnieje jawny wzór, który za chwilę uzasadnimy, jednak dla \(k > 2\) sprawa się komplikuje.
Przypadek \(k=2\)
Skupimy się teraz na przypadku \(k=2\) – to znaczy, że co druga osoba wstaje i opuszcza spotkanie. Niech \(J(n)\) oznacza pozycję (numer krzesła) osoby, która zostanie przy stole jako ostatnia. Można zauważyć, że jeśli na początku przy stole siedzi parzysta liczba osób, którą oznaczymy przez \(2n,\) to po wyproszeniu pierwszych \(n\) z nich przy stole zostanie \(n\) osób z kolejnymi numerami nieparzystymi. Jest to taka sama sytuacja, jakby na początku przy stole było \(n\) osób, tylko że ich numery są podwojone i pomniejszone o jeden. Tę obserwację można zapisać w następujący sposób: \[J(2n)=2J(n)-1.\] Kiedy na początku przy stole siedzi nieparzysta liczba osób (\(2n+1\)), po wyproszeniu \(n\) z nich przy stole zostanie \(n+1\) osób ponumerowanych kolejnymi liczbami nieparzystymi. Kolejną osobą, która zostanie wyproszona, będzie ta na pozycji \(1.\) Wtedy przy stole będzie \(n\) osób o kolejnych numerach nieparzystych, zaczynając od \(3\) – ponownie będzie to taka sama sytuacja, jakby na początku było \(n\) osób, tyle że tym razem ich numery są podwojone i powiększone o jeden: \[J(2n+1)=2J(n)+1.\] Korzystając ze wzorów \((1)\) i \((2),\) można zapisać wzór rekurencyjny: \[J(n)= \begin{cases} 1 & \text{dla } n=1, \\ 2J\left(\frac{n}{2}\right)-1 & \text{dla } n \text{ parzystego}, \\ 2J\left(\frac{n-1}{2}\right)+1 & \text{dla } n>1 \text{ nieparzystego}. \end{cases}\tag{$*$}\] Dla pierwszych szesnastu liczb całkowitych dodatnich wartości \(J(n)\) zostały zapisane w tabelce.
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| \(J(n)\) | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
W powyższej tabelce podzieliliśmy wartości funkcji \(J\) na grupy o rozmiarach będących kolejnymi potęgami dwójki. W obrębie każdej grupy wartości funkcji są kolejnymi liczbami nieparzystymi. Ta obserwacja sugeruje następującą hipotezę: \[J(2^{m}+l) = 2l+1 \;\; \text{ dla } m,l\in \mathbb{N} \text{ takich, że } 0\leq l <2^{m}.\] Prawdziwość tej hipotezy udowodnimy za pomocą indukcji względem \(m.\) W przypadku bazowym, czyli dla \(m=0,\) jedyną możliwą wartością \(l\) jest zero – wystarczy więc sprawdzić tylko jeden przypadek: \(J(1)=J(2^{0}+0)=2\cdot 0+1=1.\) Weźmy teraz dowolne \(m.\) Zakładając prawdziwość tezy dla \(m,\) udowodnimy ją dla \(m + 1.\) Najpierw zauważmy, że dla \(0 \le l < 2^{m + 1}\) nieparzystego możemy skorzystać z założenia indukcyjnego, otrzymując: \[\begin{aligned} J(2^{m+1}+l) &= 2J\left(\frac{2^{m+1}+l-1}{2}\right)+1=2J\left(2^{m}+\frac{l-1}{2}\right)+1= \\ &= 2\left(2\cdot\frac{l-1}{2}+1\right)+1=2l+1. \end{aligned}\] Jeżeli natomiast \(l\) jest parzyste, to analogicznie otrzymujemy: \[\begin{aligned} J(2^{m+1}+l) &=2J\left(\frac{2^{m+1}+l}{2}\right)-1=2J\left(2^{m}+\frac{l}{2}\right)-1= \\ &=2\left(2\cdot\frac{l}{2}+1\right)-1=2l+1. \end{aligned}\] To kończy dowód naszej hipotezy. Zauważmy, że po przekształceniu wzoru \((*)\) dostajemy wzór jawny: \[J(n) = 2(n-2^{\lfloor \log_{2}(n)\rfloor})+1,\] który pozwala nam obliczać \(J(n)\) szybciej, niż wykonując symulację wypraszania kolejnych osób, bo w czasie \(\mathcal O(1).\) Możemy się więc teraz skupić na przypadku \(k>2.\)
Przypadek \(k>2\)
Przez \(J(n,k)\) będziemy oznaczać pozycję ostatniej osoby w problemie Flawiusza dla \(n\) osób i eliminacji co \(k\)-tej osoby. Kiedy wyeliminowana zostanie \(k\)-ta osoba, w kręgu pozostanie \(n-1\) osób. Możemy teraz zamienić ich numery w ten sposób, że numeracja zaczynać się będzie od osoby na pozycji \((k \ {\rm mod}\ n) +1\) (o jeden w prawo od wyeliminowanej). Jeśli obliczymy pozycję ostatniej osoby dla mniejszego problemu \(J(n-1,k),\) to możemy łatwo otrzymać \(J(n,k),\) sprawdzając, której osobie odpowiada \(J(n-1, k)\) przed zmianą numeracji. Skoro zmiana numeracji polegała na przesunięciu numerów o \(k\) pozycji przy jednoczesnym usunięciu pozycji \(k,\) to wzór rekurencyjny przyjmuje postać: \[J(n, k) = \begin{cases} 1 & \text{dla } n = 1, \\ \Big((J(n-1, k) + k-1) \ {\rm mod}\ n\Big) +1& \text{dla } n > 1. \end{cases}\] Konieczność odejmowania i późniejszego dodawania \(1\) wynika z tego, że chcemy uniknąć wyodrębniania szczególnego przypadku, kiedy \((J(n-1,k)+k) \ {\rm mod}\ n=0\). Przy numeracji od zera wzór jest lekko zmodyfikowany i ma postać: \[J(n, k) = \begin{cases} 0 & \text{dla } n = 1, \\ (J(n-1, k) + k)\ {\rm mod}\ n & \text{dla } n > 1. \end{cases}\]
Zainteresowany Czytelnik zapewne zapyta, czy istnieje jawny wzór, gdy \(k>2.\) Okazuje się, że odpowiedź jest twierdząca dla \(k=3,\) co pokazali w 1997 roku Lorenz Halbeisen i Norbert Hungerbühler. W celu obliczenia \(J(n, 3)\) musimy najpierw znaleźć największą naturalną liczbę \(m,\) dla której \(\mathrm{round}(\alpha \cdot (\frac 32)^m) \le n,\) gdzie \(\alpha\) jest pewną obliczalną stałą w przybliżeniu równą \(\alpha \approx 0,8111\dots,\) zaś \(\mathrm{round}\) oznacza standardowe zaokrąglanie do najbliższej liczby całkowitej. Następnie definiujemy \(e = \alpha \cdot (\frac 32)^m\) oraz \(c = \mathrm{round}(\alpha \cdot (\frac 32)^m).\) Ponadto musimy zdefiniować jeszcze jedną stałą \(d\): jeśli \(e < c\) (czyli zaokrąglaliśmy w górę), to kładziemy \(d = 1,\) a w przeciwnym przypadku przyjmujemy \(d = 0.\) Ostateczny wzór na szukaną funkcję to \(J(n, 3) = 3(n - c) + d.\) Dowód wyniku Halbeisena i Hungerbühlera jest dość skomplikowany. Co więcej, jeśli chcielibyśmy zaimplementować ich wzór tak, aby działał dla dowolnego \(n,\) to musimy umieć wyliczać wartość \(\alpha\) z dowolną dokładnością. Niestety stała \(\alpha\) jest zdefiniowana jako granica pewnego ciągu zbieżnego, a autorzy nie badają problemu złożoności jej obliczania. Nadmieńmy również, że dla \(k > 3\) odpowiedź na pytanie o istnienie wzoru jawnego nie jest nam wciąż znana.
Sam wzór rekurencyjny jednak jest już bardzo cenny, gdyż można go wykorzystać do obliczania
\(J(n, k),\) używając programowania dynamicznego. Podejście to przedstawia poniższy algorytm:
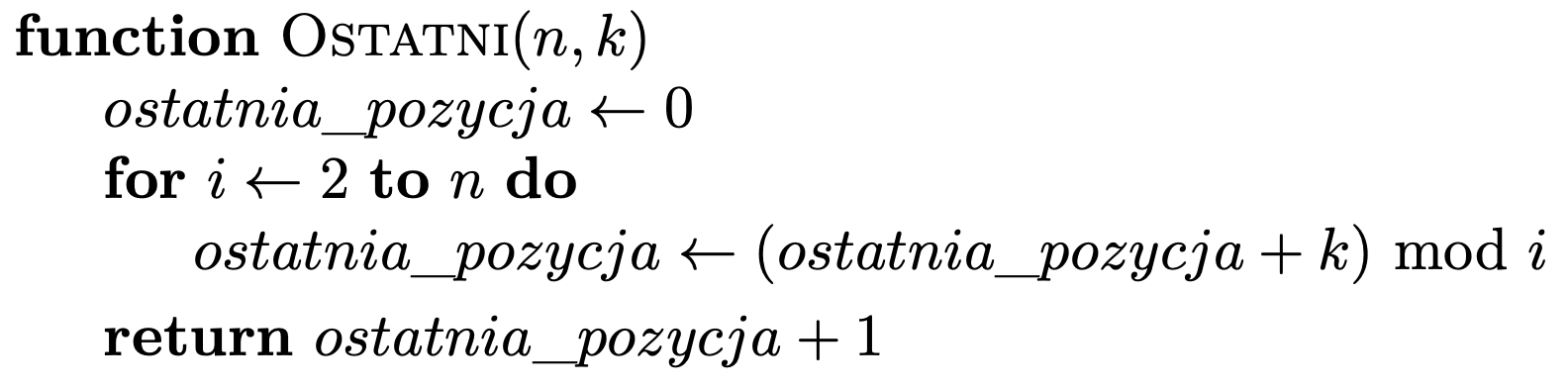Skorzystaliśmy tutaj ze wzoru rekurencyjnego dla numeracji od \(0,\) więc na koniec musieliśmy dodać \(1.\)
Zauważmy, że algorytm programowania dynamicznego ma złożoność \(\mathcal O(n).\)
Okazuje się, że zadania z konkursów programistycznych mogą prowadzić do zagadnień o złożonym charakterze kombinatorycznym. To ilustruje, jak różnorodny i nieoczywisty może być obszar nauki, który ukrywa się za pozornie prostymi problemami.