Afiliacja: CWI, Amsterdam i Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
W tym artykule przybliżymy nieco Czytelnikowi matematykę starożytnych Chin i pokażemy kilka ciekawych zagadek i problemów, które ukazały się w chińskich tekstach w okresie od 500 roku p.n.e. do XIII wieku.
W starożytnych Chinach matematycy nie byli zainteresowani podążaniem za abstrakcyjnymi pojęciami matematycznymi dla własnej satysfakcji. Kładli nacisk wyłącznie na naukę empiryczną. Stworzyli inne podejście do matematyki niż to prezentowane przez Greków, którzy byli zainteresowani także czysto teoretycznymi pytaniami (na przykład dowiedzeniem, że istnieje nieskończenie wiele liczb pierwszych lub ustaleniem liczby brył platońskich). Dlatego aby zrozumieć osiągnięcia starożytnych matematyków chińskich, trzeba skupić się na konkretnych problemach, które rozważali.
Zobacz: G.G. Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, wydanie trzecie, Princeton University Press, s. 191, 2011.
Rys. 1. Rysunek z Zhou Bi Suan Jing. Źródło: domena publiczna, Wikipedia Commons
Jednym z najstarszych zachowanych chińskich tekstów matematycznych jest Zhou Bi Suan Jing (Klasyczna Matematyka Zhou Gnomona), poświęcony astronomii i matematyce. Szacuje się, że został napisany w latach 500–200 p.n.e. Tekst zawiera interesujący rysunek (zobacz rys. 1).
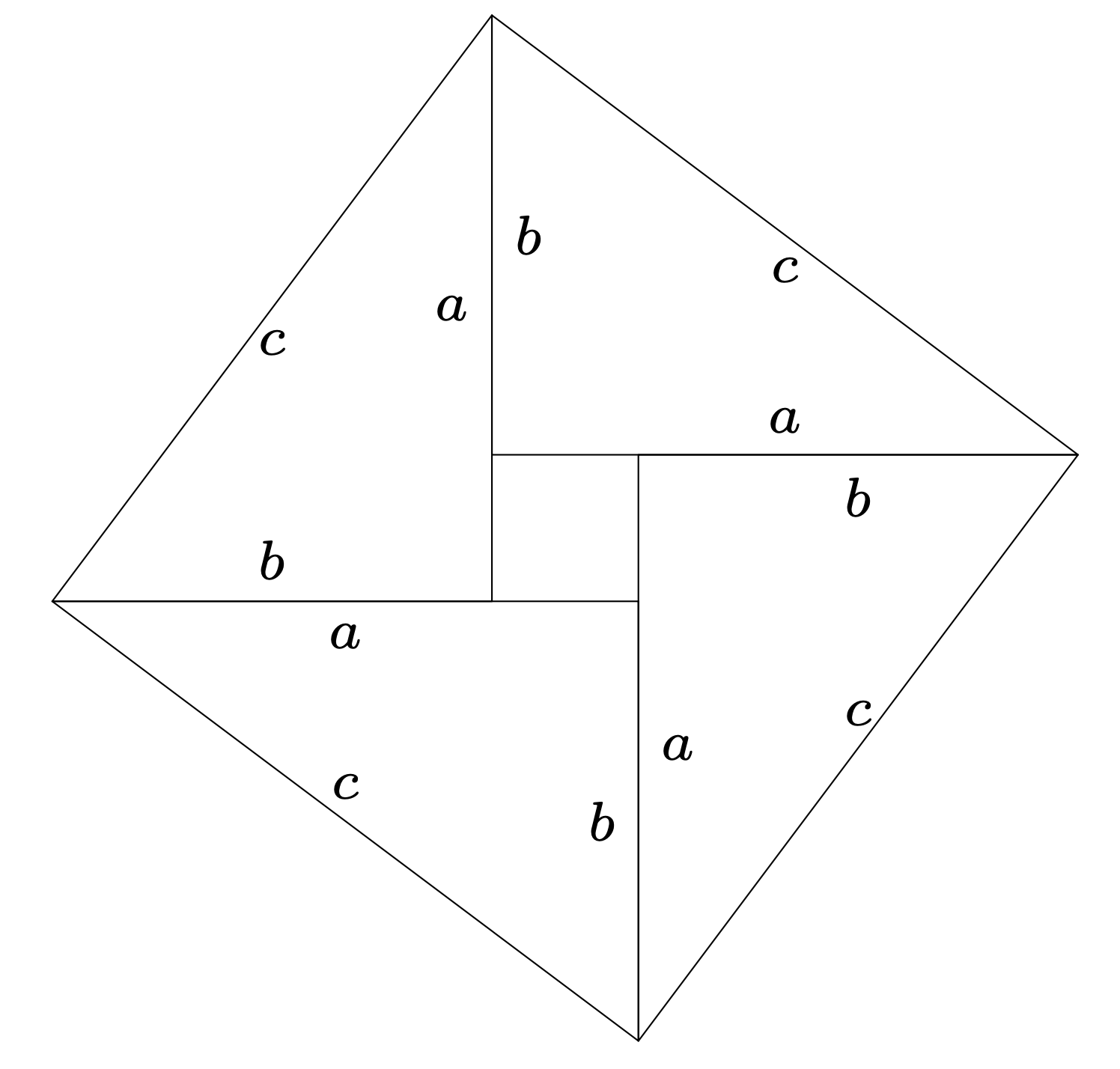
Sugeruje on elegancki dowód twierdzenia Pitagorasa. Mianowicie: rozważmy rysunek 2, gdzie oznaczamy istotne odcinki przez \(a, b\) i \(c.\)
Rys. 2. Dowód twierdzenia Pitagorasa
Pole dużego kwadratu wynosi \(c^2.\) Składa się on z czterech trójkątów prostokątnych, każdy o bokach \(a,\) \(b\) i \(c,\) oraz kwadratu o boku \(a-b.\) Stąd otrzymujemy \[4 \frac{ab}{2} + (a-b)^2 = c^2\] lub \[2ab + a^2 - 2ab + b^2 = c^2,\] co prowadzi do pożądanej konkluzji.
Najbardziej wpływowym tekstem w historii chińskiej matematyki jest anonimowa książka Jiu Zhang Suan Shu (Dziewięć Rozdziałów o Sztuce Matematycznej), napisana w latach 500 p.n.e. – 200 n.e. (za: G.G. Joseph, s. 191). Jest to właściwie kompilacja dzieł kilku pokoleń chińskich matematyków, prawdopodobnie począwszy od X wieku p.n.e. Dostępna wersja pochodzi z III wieku.
Tekst wpłynął na chińską matematykę, podobnie jak Elementy Euklidesa wpłynęły na matematykę europejską, i przez kilka wieków był używany do szkolenia urzędników administracji cesarskiej. Książka jest zorganizowana jako seria 246 problemów z rozwiązaniami, ułożonymi tematycznie w dziewięć rozdziałów.
Ostatni rozdział zawiera dowód twierdzenia Pitagorasa. Był on w szczególności wykorzystany do rozwiązania następującego pięknego problemu.
Problem złamanego bambusa
Rys. 3. Problem złamanego bambusa. Reprodukcja z książki “A Brief History of Mathematics for Curious Minds” autorstwa Krzysztofa R. Apt, za zgodą wydawcy. © 2024 World Scientific Publishing Company, https://doi.org/10.1142/13518
Poniższe sformułowanie pochodzi z XIII wieku, użyte w nim chi to jednostka długości.
Bambus o wysokości 10 chi złamał się, i jego wierzchołek dotyka ziemi 3 chi od podstawy pnia. Na jakiej wysokości się złamał?
Problem pojawiał się ponownie w pracach hinduskich matematyków, od IX do XII wieku, a ostatecznie także w niektórych tekstach w Europie. Sugeruje to migrację na zachód różnych pomysłów matematycznych ze starożytnych Chin (za: G.G. Joseph, s. 257).
Rozwiązanie problemu jest bardzo proste. Oznaczmy długość złamanej części przez \(x.\) Z twierdzenia Pitagorasa \(x^2 + 3^2 = (10-x)^2,\) czyli \({x^2 + 9 = 100-20x + x^2},\) co daje \(x = \frac{91}{20} = 4{,}55.\) A więc bambus złamał się na wysokości \(4{,}55\) chi.
Chińskie twierdzenie o reszcie
Wyrafinowanie chińskiej matematyki w IV wieku n.e. można docenić poprzez rozważenie następującego problemu z tekstu Sun Zu Suan Jing (Matematyczny podręcznik mistrza Suna):
Istnieje pewna nieznana liczba obiektów. Gdy liczymy je ,,po trzy” [tj. dzielimy przez 3], reszta wynosi 2, gdy liczymy je ,,po pięć”, reszta wynosi 3, a gdy liczymy je ,,po siedem”, reszta wynosi 2. Ile jest obiektów?
Autor tej książki podał zarówno odpowiedź, jak i wyjaśnienie swojej metody rozwiązania problemu. Rozwiązanie, gdy uogólnione do dowolnej liczby założeń postaci ,,gdy liczymy w \(x,\) reszta wynosi \(y\)”, przy założeniu, że użyte dzielniki \(y\) są względnie pierwsze, jest nazywane chińskim twierdzeniem o reszcie. Jest to ważny wynik w teorii liczb.
Najmniejszą odpowiedzią jest 23. Faktycznie, 23 podzielone przez 3 daje resztę 2, 23 podzielone przez 5 daje resztę 3, a 23 podzielone przez 7 daje resztę 2.
Problem stu ptaków
Problem stu ptaków może być sformalizowany za pomocą następujących dwóch równań: \[\begin{array}{l} 5x + 3y + \frac{1}{3} z = 100, \\ x + y +z = 100, \end{array}\] gdzie \(x, y\) i \(z\) oznaczają, odpowiednio, liczbę kogutów, kur i kurczaków.
Rozwiązania przyjmują postać: \[\begin{array}{l} x = 4t, \\ y = 25 - 7t, \\ z = 75 + 3t, \end{array}\] \(t\) jest tu całkowitym parametrem.
Wszystkie wartości, w szczególności \(y,\) muszą być nieujemne. Wynika z tego, że \(t\) musi być równe 0, 1, 2 lub 3. To prowadzi do czterech rozwiązań \((x,y,z)\) w liczbach naturalnych: \((0,25,75),\) \((4,18,78),\) \((8,11,81)\) i \((12,4,84).\) Autor pomija pierwsze z nich.
Inny słynny problem pojawił się w tekście z V wieku. Jest on sformułowany następująco (qian to miedziany pieniądz [za: G.G. Joseph, s. 288]):
Jeśli koguty kosztują 5 qianów każdy, kury kosztują 3 qiany każda i 3 kurczaki kosztują 1 qian, i jeśli 100 ptaków dostaje się za 100 qianów, ile jest kogutów, kur i kurczaków?
Tekst oferuje trzy rozwiązania tego problemu, chociaż nie podano wyjaśnienia, jak zostały one otrzymane. Matematycznie ten problem jest interesujący, ponieważ wymaga rozwiązania równań liniowych w liczbach naturalnych, czyli tak zwanych równań diofantycznych, rozważanych w Starożytnej Grecji przez Diofantosa (ok. 250 roku). Co więcej, sformalizowanie problemu jako dwóch równań z trzema zmiennymi prowadzi do koncepcji parametryzowanych rozwiązań. Co ciekawe, warianty tego problemu pojawiły się kilka wieków później w Indiach, Egipcie i średniowiecznej Europie.
Problem miasta otoczonego murem
Rys. 4. Problem miasta otoczonego murem. Źródło: domena publiczna, Wikipedia Commons
Zakończmy tę krótką prezentację omówieniem następującego intrygującego problemu z okresu średniowiecza. Pochodzi on z imponującego tekstu Shu Shu Jiu Zhang (Traktat matematyczny w dziewięciu sekcjach), napisanego w XIII wieku przez Chińskiego matematyka Qin Jiushao (ok. 1202 – ok. 1261). Książka zawiera 81 problemów matematycznych dotyczących różnych zagadnień praktycznych, w tym astronomii i spraw wojskowych. W zadaniu poniżej li jest jednostką odległości.
Miasto jest otoczone okrągłym murem o nieznanej średnicy, z czterema bramami. Drzewo leży 3 li na północ od północnej bramy. Jeśli idziemy 9 li na wschód od południowej bramy, drzewo staje się widoczne. Znajdź średnicę miasta.
Zobacz: rozdział 5 w książce C. Smoryńskiego History of Mathematics: A Supplement, Springer, 2008.
Ten problem został szczegółowo omówiony w książce C. Smoryńskiego. Przedstawimy tu alternatywne rozwiązanie, które wykorzystuje tożsamość trygonometryczną dotyczącą funkcji tangens, \(\tan.\)
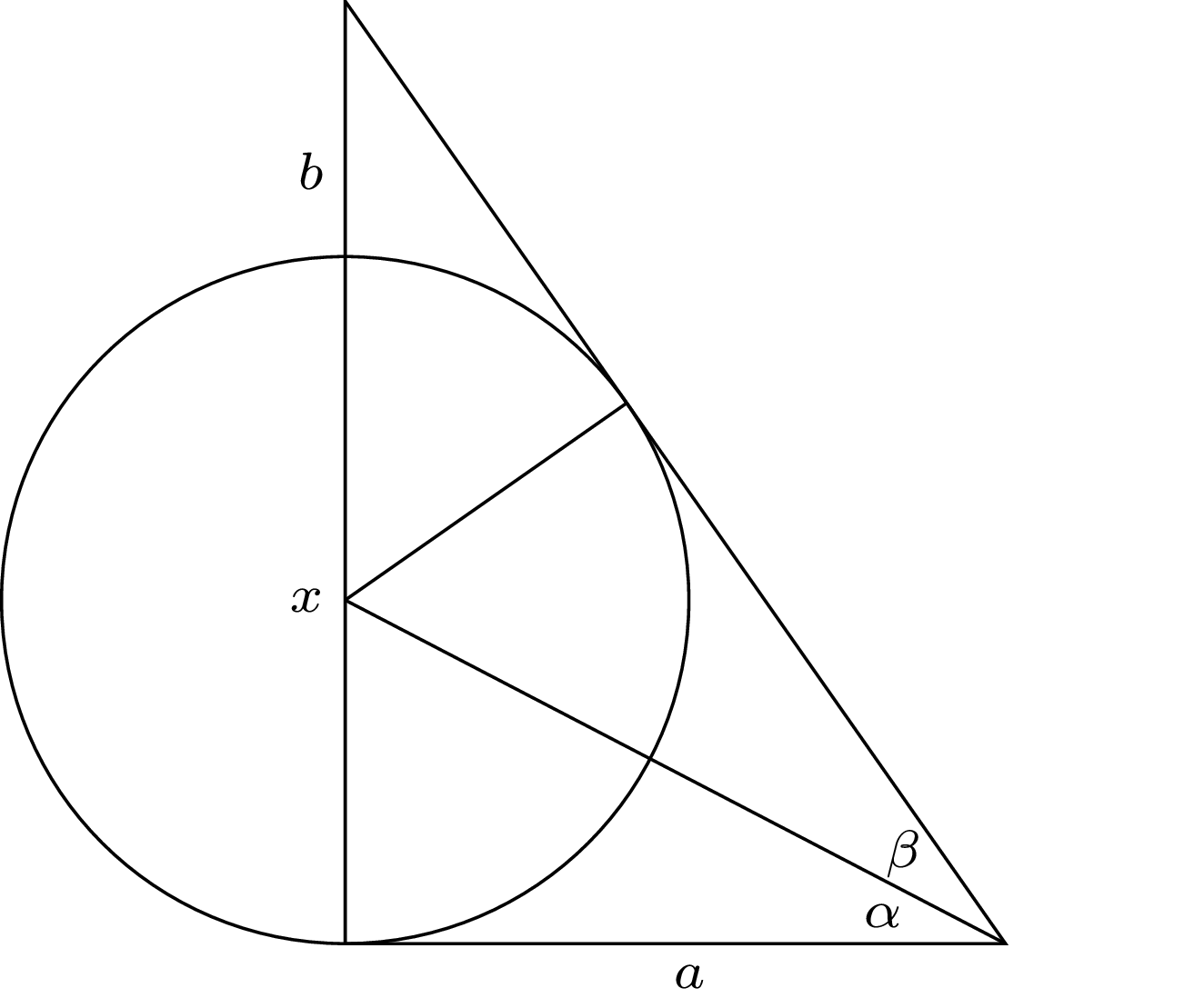
Rozważmy uogólnienie, w którym używamy dowolnych wartości \(a\) i \(b\) zamiast \(9\) i \(3.\) Zadanie sprowadza się więc do obliczenia średnicy \(x\) okręgu, gdy mamy dane \(a\) i \(b.\) Dodajmy do początkowego rysunku dodatkowy promień okręgu, jak w rysunku 5.
Rys. 5. Problem okrągłego miasta otoczonego murem w ogólnej wersji
Rozważmy trójkąty prostokątne o kątach \(\alpha\) i \(\beta.\) Mają one wspólny jeden bok i w każdym z nich drugi bok jest równy promieniowi okręgu. Wobec tego z twierdzenia Pitagorasa trzecie boki są sobie równe.
A więc te trójkąty są przystające, zatem \(\alpha = \beta.\) Mamy \(\tan(2 \alpha) = \frac{x + b}{a}\) oraz \(\tan(\alpha) = \frac{\frac{x}{2}}{a},\) więc \[\tan(2 \alpha) = 2 \tan(\alpha) + \frac{b}{a}.\] Korzystamy teraz z tożsamości trygonometrycznej \[\tan(2 \alpha) = \frac{2 \tan(\alpha)}{1 - \tan^2(\alpha)}.\] Ostatnie dwie równości prowadzą do równania \[2 y + \frac{b}{a} = \frac{2 y}{1 - y^2},\] gdzie \(y = \tan(\alpha).\)
Mnożąc obie strony przez \(a(1 - y^2)\) i upraszczając, otrzymujemy równanie trzeciego stopnia w \(y\): \[2ay^3 + by^2 - b = 0.\]
Ale \(y = \frac{\frac{x}{2}}{a},\) więc podstawiając, otrzymujemy po uproszczeniu następujące równanie trzeciego stopnia w \(x\): \[x^3 + bx^2 - 4a^2b = 0.\]
Dla \(a = 9\) i \(b = 3\) za pomocą WolframAlpha, https://www.wolframalpha.com, otrzymujemy trzy rozwiązania: dwa w liczbach zespolonych i jedno w liczbach rzeczywistych, \(x = 9,\) co jest poszukiwaną odpowiedzią.
Fakt, że rozwiązanie tak prostego problemu wymaga rozważenia równania trzeciego stopnia, jest zaskakujący. Drogi Czytelniku, jeżeli uda Ci się rozwiązać ten problem przy użyciu tylko równania drugiego stopnia, to daj, proszę, znać na adres apt@cwi.nl.
Tekst oparty na rozdziale 3 i załącznikach 3 i 17 z książki: Krzysztof R. Apt, ,,A Brief History of Mathematics for Curious Minds”, World Scientific, 2024.