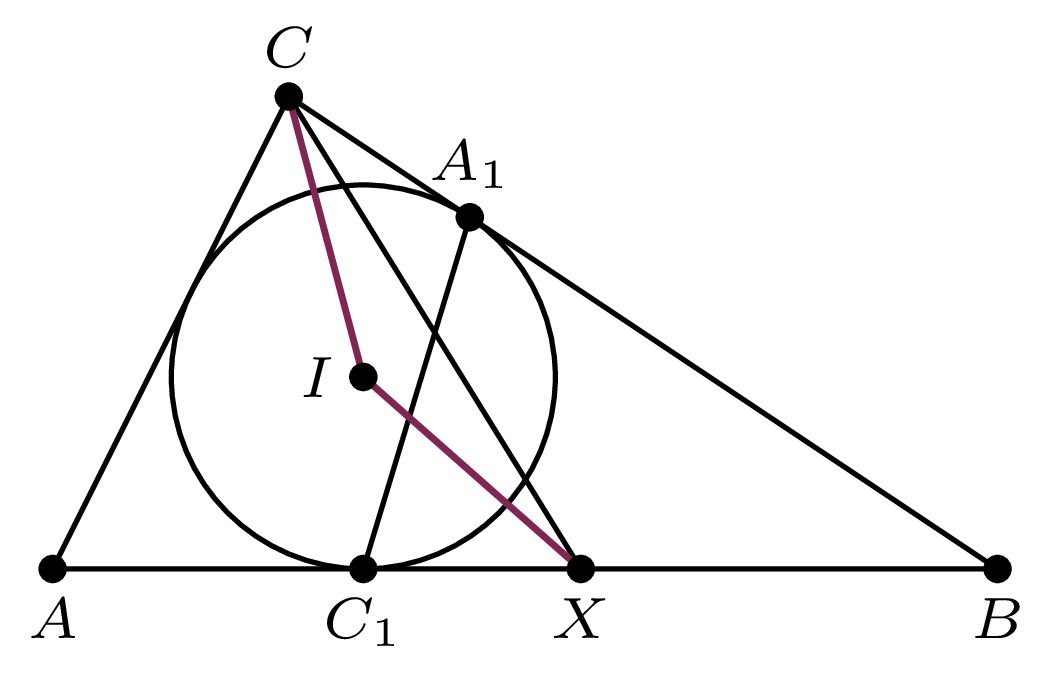
Okrąg o środku w punkcie \(I\) jest wpisany w trójkąt \(ABC\) i jest styczny do boków \(BC\) i \(AB\) odpowiednio w punktach \(A_1\) i \(C_1.\) Na odcinku \(BC_1\) obrano punkt \(X\) taki, że \(IX = IC.\) Udowodnić, że środek odcinka \(XC\) leży na odcinku \(A_1C_1.\)
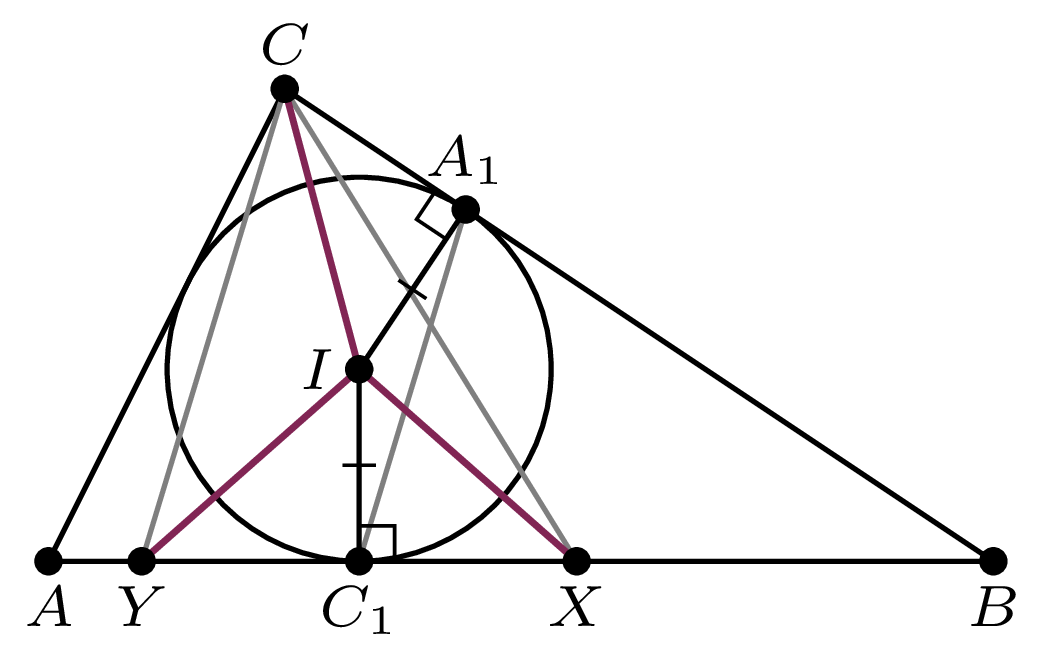
Trójkąty prostokątne \(XIC_1\) i \(CIA_1\) są przystające, gdyż mają równe przeciwprostokątne \(IX,\) \(XC\) oraz przyprostokątne równe promieniowi okręgu wpisanego w trójkąt \(ABC.\) Zatem \(C_1 X = A_1 C.\)
Niech punkt \(Y\) będzie punktem symetrycznym do punktu \(X\) względem \(C_1.\) Wtedy czworokąt \(A_1CYC_1\) jest symetryczny względem dwusiecznej kąta \(B\) (ponieważ \(C_1 Y = A_1 C\) oraz \(BC_1 = BA_1\)), zatem \(A_1 C_1 \parallel CY.\) Oznacza to, że prosta \(C_1A_1\) jest prostą łączącą środki boków \(YX\) i \(XC\) trójkąta \(YXC.\)
Uwaga: Można również zauważyć, że na czworokącie \(BXIC\) można opisać okrąg, wtedy prosta \(A_1C_1\) jest prostą Simsona punktu \(I\) (patrz Deltoid z \(\Delta^{10}_{15}\)) względem trójkąta \(BXC.\)
Funkcja \(f\colon \mathbb{R}\to \mathbb{R}\) dla wszystkich \(x,y \in \mathbb{R}\) spełnia nierówność \[f(x^2+2y) \geq f(x^2+3y).\] Udowodnić, że \(f\) jest funkcją stałą na zbiorze dodatnich liczb rzeczywistych.
Niech teraz \(0 < u < v.\) Wtedy znajdziemy taką liczbę całkowitą dodatnią \(n,\) że \[\left(\frac{3}{2}\right)^{n-1}\leq \frac{v}{u} < {\left(\frac{3}{2}\right)^{n}}.\] Podstawiając \(x=0\) oraz \(y=\frac{1}{2}z,\) dostajemy \(f(z)\geq f\left(\frac{3}{2}z\right)\) dla dowolnej liczby rzeczywistej \(z,\) a zatem \[\begin{split} f(u) \geq f\left(\frac{3}{2}u\right)\geq f\biggl(\left(\frac{3}{2}\right)^2 u\biggr) \geq \ldots \geq f\left(\left(\frac{3}{2}\right)^n u\right)\geq f(v)\geq f(u), \end{split}\] gdzie w ostatnich dwóch nierównościach wykorzystaliśmy pokazaną monotoniczność \(f.\) Wobec tego \(f(u)=f(v).\)
Każdy wierzchołek \(n\)-kąta wypukłego \(\mathcal{F}\) (\(n\geq 4\)) malujemy na biało lub czarno. Przekątną \(\mathcal{F}\) nazwiemy kolorową, jeśli jej końce są różnego koloru. Kolorowanie wszystkich wierzchołków \(\mathcal{F}\) nazwiemy dobrym, jeśli \(\mathcal{F}\) można podzielić na trójkąty kolorowymi przekątnymi, które nie mają punktów wspólnych innych niż wierzchołki \(\mathcal{F}.\) Wyznaczyć liczbę dobrych kolorowań.
Powiemy, że bok wielokąta jest kolorowy, jeśli jego końce są w różnych kolorach, a niekolorowy – w przeciwnym razie. Kolorowanie wierzchołków nazwiemy uporządkowanym, jeśli istnieje prosta oddzielająca białe wierzchołki od czarnych.
Pokażemy, że kolorowanie wierzchołków wypukłego \(n\)-kąta (dla \(n\geq 3\)) jest dobre wtedy i tylko wtedy, gdy jest uporządkowane. Istotnie, załóżmy, że pokolorowanie wierzchołków wypukłego \(n\)-kąta jest dobre, i rozważmy odpowiedni podział wielokąta na trójkąty kolorowymi przekątnymi. W takim podziale będzie dokładnie \(n-2\) trójkątów. W każdym z tych trójkątów można wybrać odcinek łączący wierzchołki tego samego koloru. Odcinek ten nie może być przekątną \(n\)-kąta, dlatego jest to jego niekolorowy bok. Tak więc dla każdego z \(n-2\) trójkątów istnieje niekolorowy bok \(n\)-kąta (dla różnych trójkątów boki te są oczywiście różne), zatem w naszym \(n\)-kącie jest co najmniej \(n-2\) niekolorowych boków. Równoważnie, są w nim co najwyżej dwa kolorowe boki, skąd łatwo wynika, że kolorowanie to jest uporządkowane.
Załóżmy teraz, że kolorowanie wierzchołków wypukłego \(n\)-kąta jest uporządkowane, oznaczmy kolejno wierzchołki \(A_1, A_2,\ldots,A_{k}\) (białe), \(B_{1}, B_{2},\ldots, B_{l}\) (czarne). Narysujmy wszystkie przekątne od \(A_1\) do czarnych wierzchołków i wszystkie przekątne od \(B_1\) do białych wierzchołków. W ten sposób otrzymujemy dobry podział naszego wielokąta.
Pozostaje obliczyć liczbę uporządkowanych kolorowań \(n\)-kąta. Dla każdej możliwej liczby \(k\) czarnych wierzchołków (\(k\) przyjmuje wartości od 1 do \(n -1\)) spośród wszystkich \(n\) wierzchołków można na \(n\) sposobów wybrać układ bloków \(k\) kolejnych czarnych wierzchołków, tj. liczba uporządkowanych kolorowań wynosi \(n (n-1).\)
Pokonywanie zakrętu ze zbyt dużą prędkością kończy się poślizgiem i wypadnięciem z łuku drogi lub przewróceniem pojazdu (tzw. dachowaniem). Znajdź warunki, w jakich następuje pierwszy lub drugi przypadek. Samochód o masie \(m\) pokonuje zakręt o promieniu \(R\) z prędkością \(v,\) współczynnik tarcia opon o powierzchnię drogi wynosi \(f,\) a przyspieszenie ziemskie \(g.\) Droga jest pozioma. Środek masy pojazdu znajduje się na wysokości \(h\) nad drogą, w połowie odległości \(d\) między kołami.
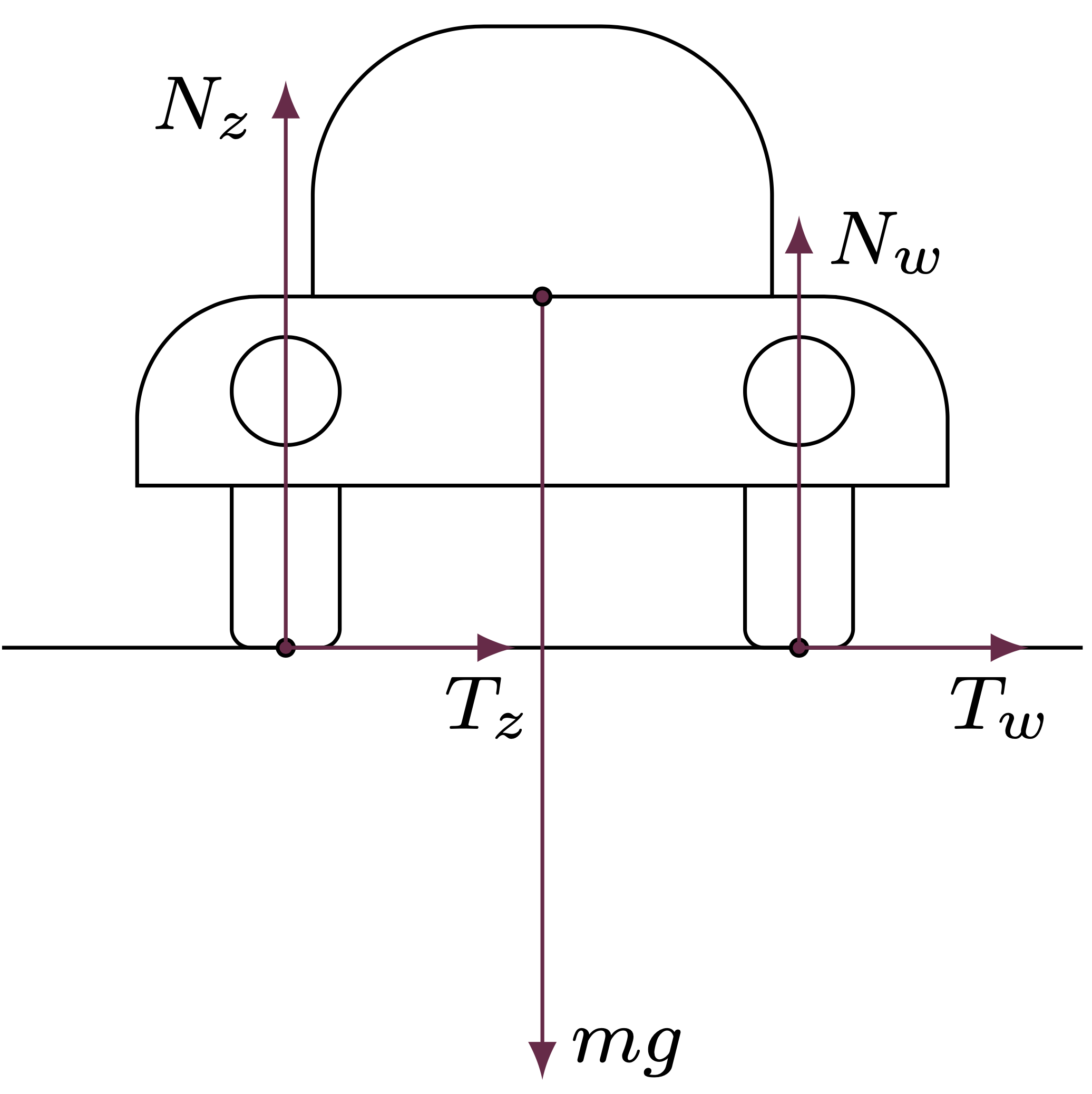 Rysunek przedstawia siły działające na samochód podczas pokonywania zakrętu ‑ środek łuku jest po prawej stronie. Pionowe składowe sił równoważą ciężar samochodu: \[N_z + N_w = mg ,\] a poziome składowe (siły tarcia) są źródłem siły dośrodkowej: \[T_z + T_w = \frac{mv^2}{R}.\]
Dodatkowo wiemy, że suma momentów tych sił podczas stabilnej jazdy (obliczymy tę sumę względem środka masy samochodu) wynosi zero:
\[(N_w - N_z)\frac{d}{2} + (T_w + T_z)h = 0.\]
Otrzymany układ równań pozwala wyznaczyć \(N_w\) i \(N_z\):
\[N_z = \frac{mg}{2} + \frac{mv^2h}{d\cdot R};\ \ \ N_w = \frac{mg}{2} - \frac{mv^2h}{d\cdot R}.\]
Rysunek przedstawia siły działające na samochód podczas pokonywania zakrętu ‑ środek łuku jest po prawej stronie. Pionowe składowe sił równoważą ciężar samochodu: \[N_z + N_w = mg ,\] a poziome składowe (siły tarcia) są źródłem siły dośrodkowej: \[T_z + T_w = \frac{mv^2}{R}.\]
Dodatkowo wiemy, że suma momentów tych sił podczas stabilnej jazdy (obliczymy tę sumę względem środka masy samochodu) wynosi zero:
\[(N_w - N_z)\frac{d}{2} + (T_w + T_z)h = 0.\]
Otrzymany układ równań pozwala wyznaczyć \(N_w\) i \(N_z\):
\[N_z = \frac{mg}{2} + \frac{mv^2h}{d\cdot R};\ \ \ N_w = \frac{mg}{2} - \frac{mv^2h}{d\cdot R}.\]
Mamy dodatkowo \(T_w + T_z \le f(N_w + N_z),\) a stąd warunkiem braku poślizgu jest \(v^2 \le gRf.\) Dachowanie zacznie się, gdy \(N_w = 0,\) co prowadzi do warunku: \(v^2 \le gRd/(2h).\)
Wniosek: jeśli \(f < d/(2h),\) to przy nadmiernej prędkości nastąpi poślizg, a gdy \(f > d/(2h),\) to nastąpi dachowanie. Dlatego ciężarówki i SUV-y (duża wartość \(h\)) częściej dachują niż ,,zwykłe” samochody osobowe. Dodatkowy bagażnik na dachu samochodu ,,sprzyja” dachowaniu.
W rozwiązaniu pominięte zostało niebezpieczeństwo poślizgu prowadzącego do obrotu wokół osi prostopadłej do drogi związane z nierównomiernym rozkładem masy pojazdu i nieumiejętnym używaniem pedału gazu.
W wyniku zderzeń neutronów promieniowania kosmicznego z atomami
atmosferycznego azotu \(^{14}\)N powstają atomy węgla \(^{14}\)C, które reagują z atmosferycznym tlenem, tworząc cząsteczki dwutlenku węgla CO\(_2.\) Izotop \(^{14}\)C jest nietrwały i w przemianie \(\beta^-\) rozpada się do \(^{14}\)N z czasem połowicznego zaniku \(\tau_{1/2} = 5730\) lat. Ogromna większość cząsteczek CO\(_2\) w atmosferze zawiera stabilny izotop \(^{12}\)C, przy czym stosunek liczb cząsteczek z atomami \(^{14}\)C i \(^{12}\)C pozostaje stały w czasie (dynamiczna równowaga procesów tworzenia i rozpadu \(^{14}\)C). W wyniku fotosyntezy w takim samym stosunku izotopy węgla są przyswajane przez organizmy żywe (dopóki pozostają żywe).
W ruinach starożytnego miasta archeolodzy znaleźli papirusowy zwój, w którym stosunek atomów \(^{14}\)C i \(^{12}\)C wynosił 80% wartości mierzonej we współczesnych roślinach. Kiedy powstał badany zwój?
Uwaga: zawartość izotopu \(^{14}\)C w próbce określa się, mierząc liczbę rozpadów \(\beta^-\) lub rozdzielając w separatorze mas izotopy zawarte w węglu wyizolowanym z próbki.