*Kopenhaga
Na prostej siedzi \(n\) identycznych pcheł (na tyle małych, że może ich być nawet po kilka w jednym punkcie). Pchły mają kiepski wzrok i widzą tylko na odległość 1. W pewnej chwili wszystkie pchły wykonują jednocześnie następującą operację. Każda pchła rozgląda się na prawo i lewo, rejestruje pozycje wszystkich pcheł, które widzi (w tym swoją własną i być może innych pcheł siedzących w tym samym punkcie), i oblicza średnią arytmetyczną tych pozycji. Inaczej mówiąc: wyznacza środek ciężkości pcheł będących w zasięgu jej wzroku. Następnie na komendę wszystkie pchły przeskakują – hop! – każda do wyliczonego przez siebie punktu. Potem cały proces powtarza się znowu i znowu, w kolejnych chwilach czasu \(t=1,2,\ldots\)
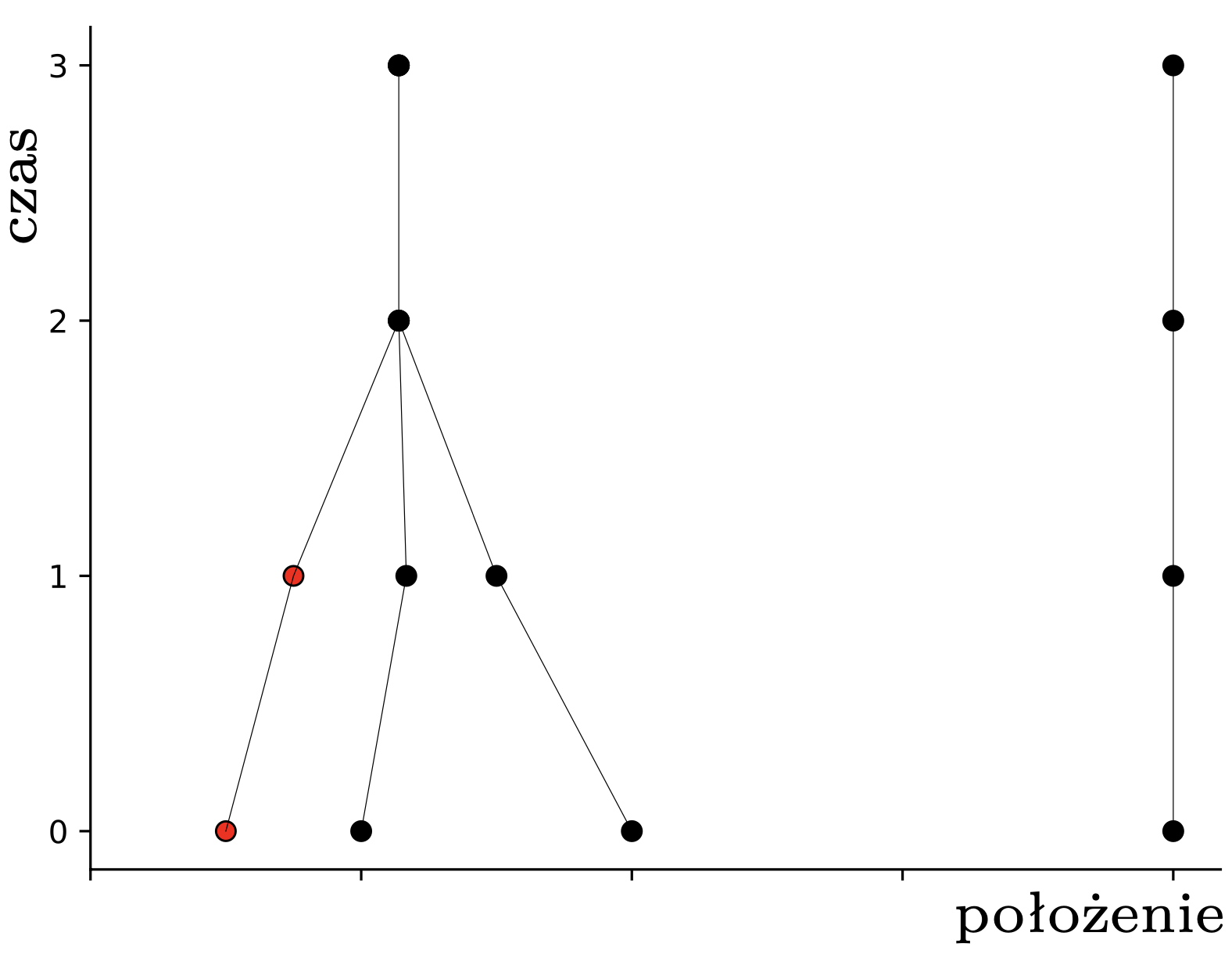
Rys. 1. Pchły \(A,B,C,D\) (w dolnym rzędzie w chwili \(t=0\)) i ich trajektorie w czasie (oś pionowa)
Dla ilustracji rozważmy \(4\) pchły \(A,B,C,D\) startujące w punktach \(\frac12,\) \(1,\) \(2\) i \(4\) (rys. 1). Pchła \(A\) widzi \(A\) i \(B,\) pchła \(B\) widzi \(A,\) \(B\) i \(C,\) zaś pchła \(C\) widzi \(B\) i \(C.\) Pchła \(D\) widzi tylko siebie. Zatem po pierwszym gwizdku pchły przeskoczą kolejno do nowych pozycji:
pchła \(A\): \(\frac12(\frac12 + 1) = \frac{3}{4}.\)
pchła \(B\): \(\frac13(\frac12 + 1 + 2) = 1\frac{1}{6}.\)
pchła \(C\): \(\frac12(1 + 2) = 1\frac{1}{2}.\)
pchła \(D\): \(\frac{4}{1} = 4.\)
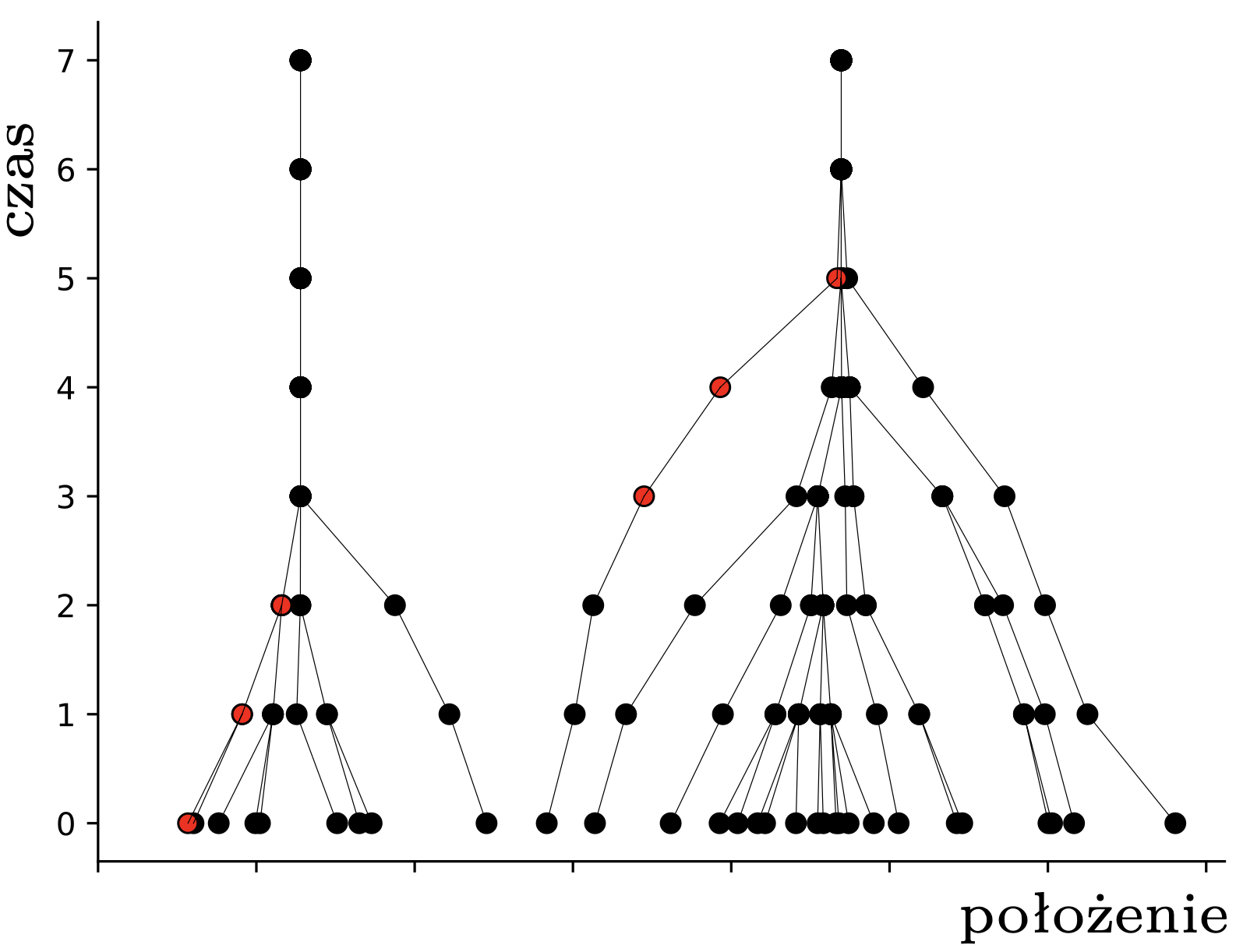
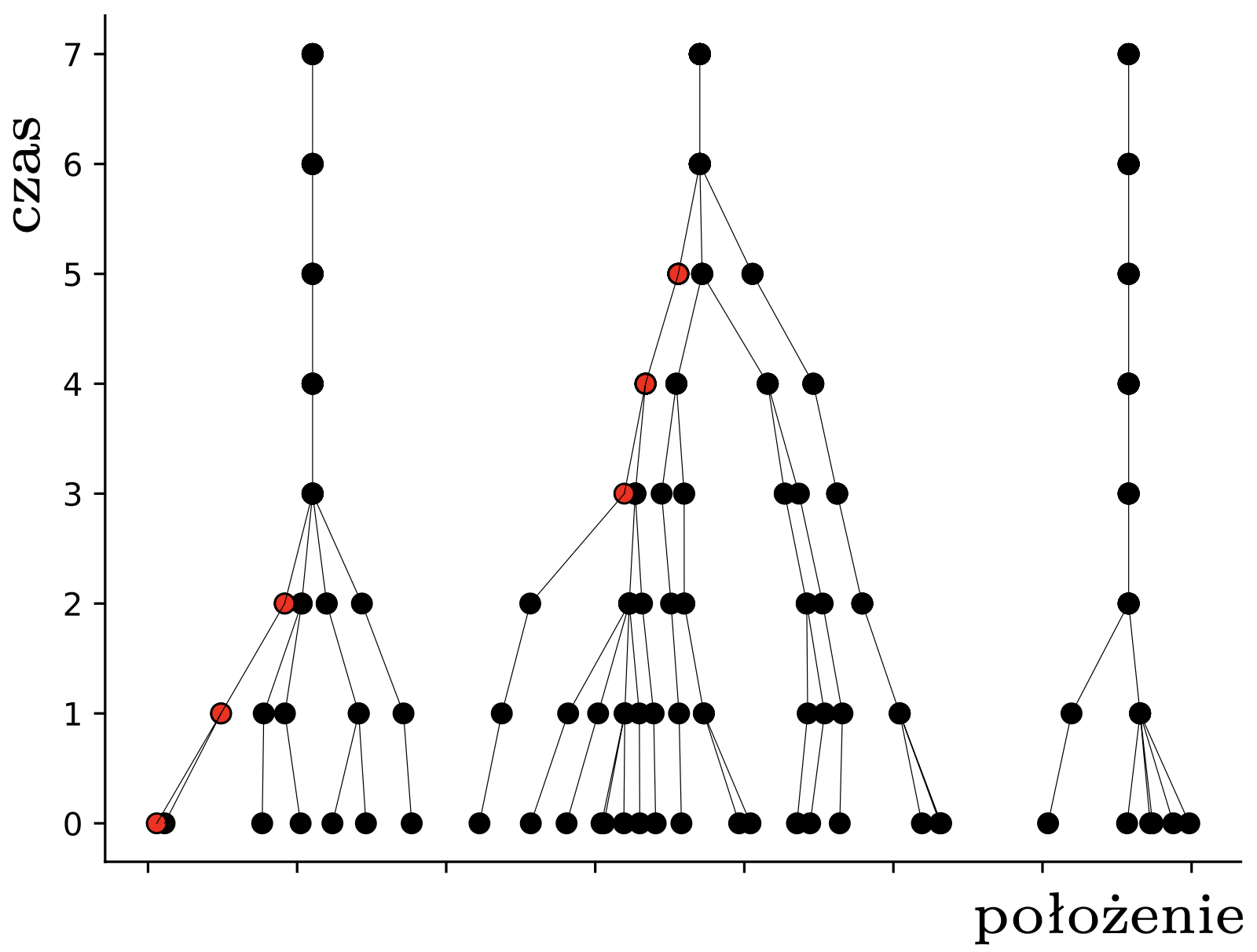
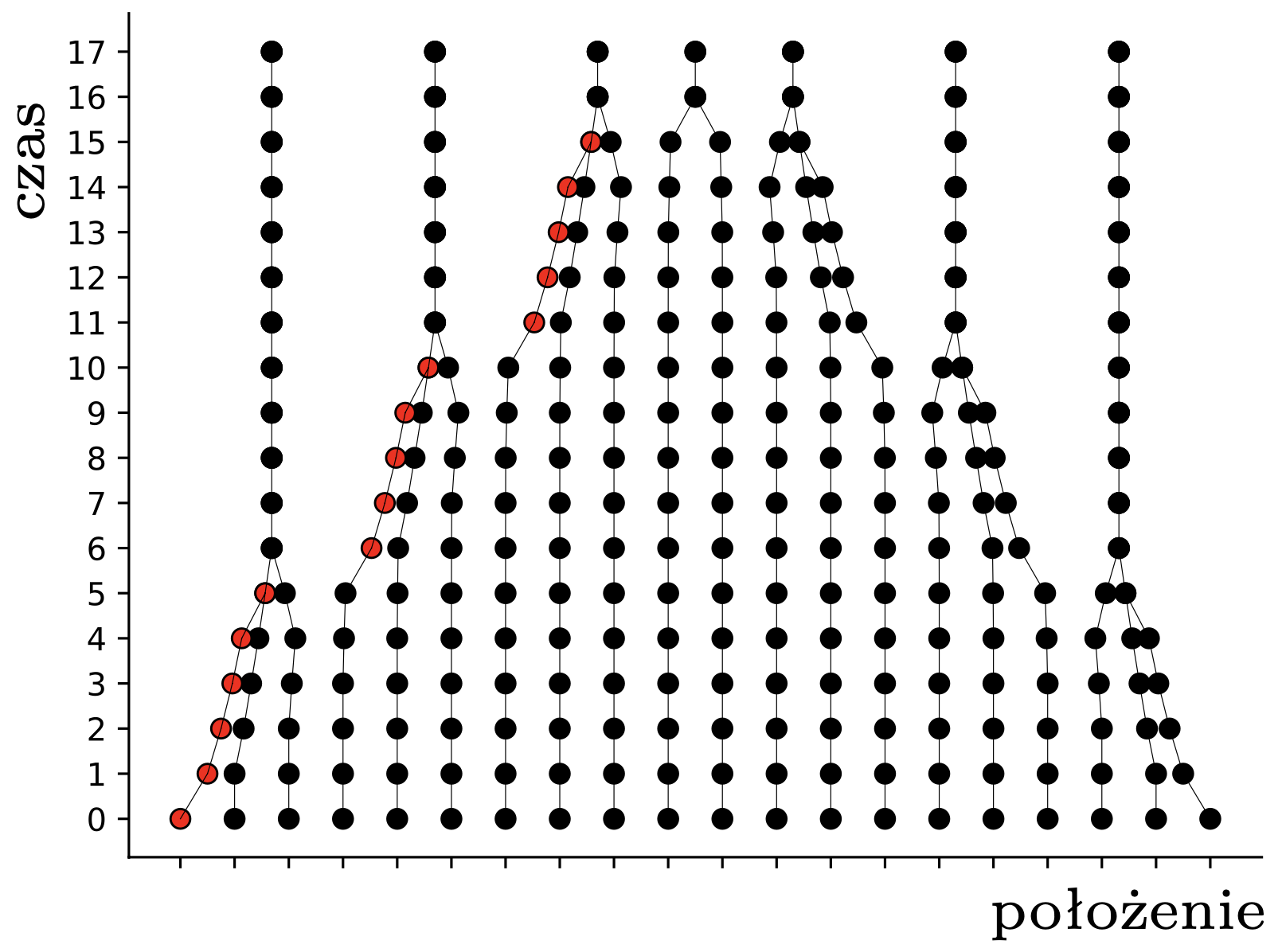
W tym momencie pchły \(A,B,C\) znajdują się w obrębie wspólnego przedziału o długości \(1,\) więc widzą się wszystkie nawzajem i nie widzą nikogo innego. To oznacza, że w następnym kroku wszystkie obliczą ten sam środek ciężkości: \[\frac13\left(\frac{3}{4}+1\frac{1}{6}+1\frac{1}{2}\right) = 1\frac{5}{36},\] i skoczą do tego punktu. Pchła \(D\) nadal się nie rusza. W kolejnym kroku, i we wszystkich następnych, już nic się nie zmieni – każda pchła będzie podskakiwać w miejscu. Pchły, które już nigdy nie zmienią pozycji, nazwiemy uziemionymi; pchła \(D\) była uziemiona od początku, a pchły \(A,B,C\) po drugim skoku. Sytuację, w której wszystkie pchły są uziemione, nazwiemy stabilną. Na rysunku 2 widzimy ewolucję większych losowych układów \(30\) pcheł o pozycjach początkowych w przedziale \([0,7].\)
Rys. 2. Przykładowe trajektorie pcheł. Znaczenie czerwonych kropek wyjaśnimy później
Opisany przez nas proces to najprostszy wariant tak zwanego modelu Hegselmanna–Krausego (w skrócie HK). Jego autorom nie chodziło jednak o tresurę pcheł, ale o matematyczne modelowanie dynamiki opinii (ang. opinion dynamics), a konkretnie polaryzacji poglądów. Model ten opiera się na założeniu, że nasze opinie na dany temat zmieniamy, dostosowując je (poprzez uśrednianie) do opinii innych osób o w miarę zbliżonym nastawieniu. Przypuśćmy na przykład, że każdy z nas ma swoje zdanie na temat kisielu, wyrażone liczbą rzeczywistą między 0 (nienawidzę) a 10 (mógłbym jeść cały czas). Załóżmy, że oceniamy kisiel umiarkowanie, na 4. W modelu HK będziemy z czasem powoli zmieniać swój punkt widzenia pod wpływem otoczenia. Zakładając dalej, że zwykliśmy wchodzić w interakcje z osobami o zbliżonych poglądach na kisiel (powiedzmy mieszczących się w przedziale \([3,5]\)) i nie traktujemy serio \(10\)-punktowych kisielowych ekstremistów, dochodzimy do pomysłu HK, że naszą opinię zastępujemy średnią opinią naszego kisielowego sąsiedztwa. Hop!
Oczywiście dynamika opinii interesuje się ewolucją naszych poglądów na ważkie tematy polityczne, ekonomiczne, społeczne, a nie na kisiel. Co więcej, nasze opinie są zwykle wielowymiarowe, to znaczy opisane wektorem w \(\mathbb{R}^m,\) w którym poszczególne współrzędne określają nasze stanowisko wobec \(m\) różnych zagadnień (tu akurat nasz model w oczywisty sposób się uogólnia). Oczywiście modele socjologiczne opisują statystyczne trendy, a nie zachowanie jednostek – ja na przykład oceniam kisiel na 0 i nigdy w życiu nie zmienię zdania, niezależnie od tego, co myślą o tym Hegselmann i Krause. Nie zmienia to faktu, że jednowymiarowy model HK – najprostszy w bogatej hierarchii modeli – jest sam w sobie ciekawym obiektem matematycznym, więc warto przyjrzeć mu się przez chwilę.
Pierwsze pytanie, które zadają sobie Hegselmann i Krause, i na które postaramy się odpowiedzieć także my, brzmi: czy każda początkowa konfiguracja pcheł osiąga stan stabilny, a jeśli tak, to jak szybko?
Rozpocznijmy od kilku prostych obserwacji, których precyzyjne uzasadnienia pozostawiamy jako ćwiczenie. Od razu widzimy, że pchły nigdy nie opuszczą przedziału, który zajmowały na początku, pomiędzy pozycjami startowymi najbardziej skrajnych pcheł na lewo i prawo. Jeżeli pewne dwie kolejne pchły są rozdzielone pustym odcinkiem długości większej niż \(1,\) to cały układ rozpada się na dwa niezależne systemy (na lewo i prawo od tej przerwy), które nigdy nie wejdą ze sobą w żadną interakcję. Szczególnym przypadkiem tej sytuacji jest grupa pcheł uziemionych razem w jednym punkcie – mają one pustą przestrzeń długości większej niż \(1\) po obu stronach. Zauważmy też, że pchły nie mogą zamienić się kolejnością – jeżeli dwie pchły zajmują pozycje \(p_1, p_2\) przed skokiem i odpowiednio \(p_1',p_2'\) po skoku, to \(p_1\leq p_2\) implikuje \(p_1'\leq p_2'.\) Pchły, które spotkają się w jednym punkcie, będą już zawsze podróżować razem. Wreszcie odnotujmy, że w jednym skoku pchła może przeskoczyć co najwyżej o odległość \(1-\frac{1}{n}\); ma to miejsce w ekstremalnym przypadku, gdy pojedyncza pchła ma wszystkie \(n-1\) pozostałych pcheł dokładnie na jednym z krańców swojego pola widzenia.
Żeby uprościć dalszą dyskusję, umówmy się, że utożsamiamy pchły z ich pozycjami, a gdy trzeba wybrać jedną z pcheł siedzących w tym samym punkcie, bierzemy którąkolwiek.
Przed każdą rundą znajdujemy najbardziej wysuniętą na lewo spośród wszystkich jeszcze nieuziemionych pcheł i nakładamy jej na głowę czerwoną czapeczkę (jeśli takiej pchły nie ma, to stan jest już stabilny). Te pchły zaznaczyliśmy na czerwono na towarzyszących tekstowi rysunkach. Zauważmy, że pchła w czerwonej czapeczce zawsze skacze ostro w prawo i albo zachowuje czapeczkę na następną rundę, albo, jeśli została właśnie uziemiona, czapeczka przechodzi na którąś pchłę daleko w prawo (więcej niż 1 cm), albo osiągamy stan stabilny. Tak czy inaczej, w każdym kroku, w którym jeszcze coś się dzieje, czapeczka wędruje ostro w prawo. Jeśli uda nam się pokazać, że te przesunięcia muszą być stosunkowo duże, to możemy wnioskować, że będzie ich tylko skończenie wiele, bo czapeczka nie może zawędrować poza początkową pozycję skrajnie prawej pchły. Intuicyjnie idea jest następująca: przypuśćmy, że w pewnym ruchu pchła z czapeczką przesunęła się tylko o bardzo, bardzo mało. Wtedy wszystkie jej sąsiadki musiały być bardzo, bardzo blisko niej, i jedynym sposobem, aby całe to towarzystwo nie zostało przez tę bliskość razem uziemione, jest istnienie pchły tuż poza zasięgiem wzroku pchły z czapeczką (a więc daleko), odciągającej niektóre jej sąsiadki trochę w prawo. Jednak to ,,trochę” wystarczy, aby w następnym ruchu pchła z czapeczką musiała skoczyć wyraźnie dalej. Pora na szczegóły; jak się okaże, ,,bardzo, bardzo blisko”, ,,trochę w prawo” i ,,wyraźnie dalej” będą naprawdę małe, ale jednak jednostajnie odgraniczone od zera, i to wystarczy.
Pchła w czerwonej czapeczce wygenerowana przez AI (visme.co)
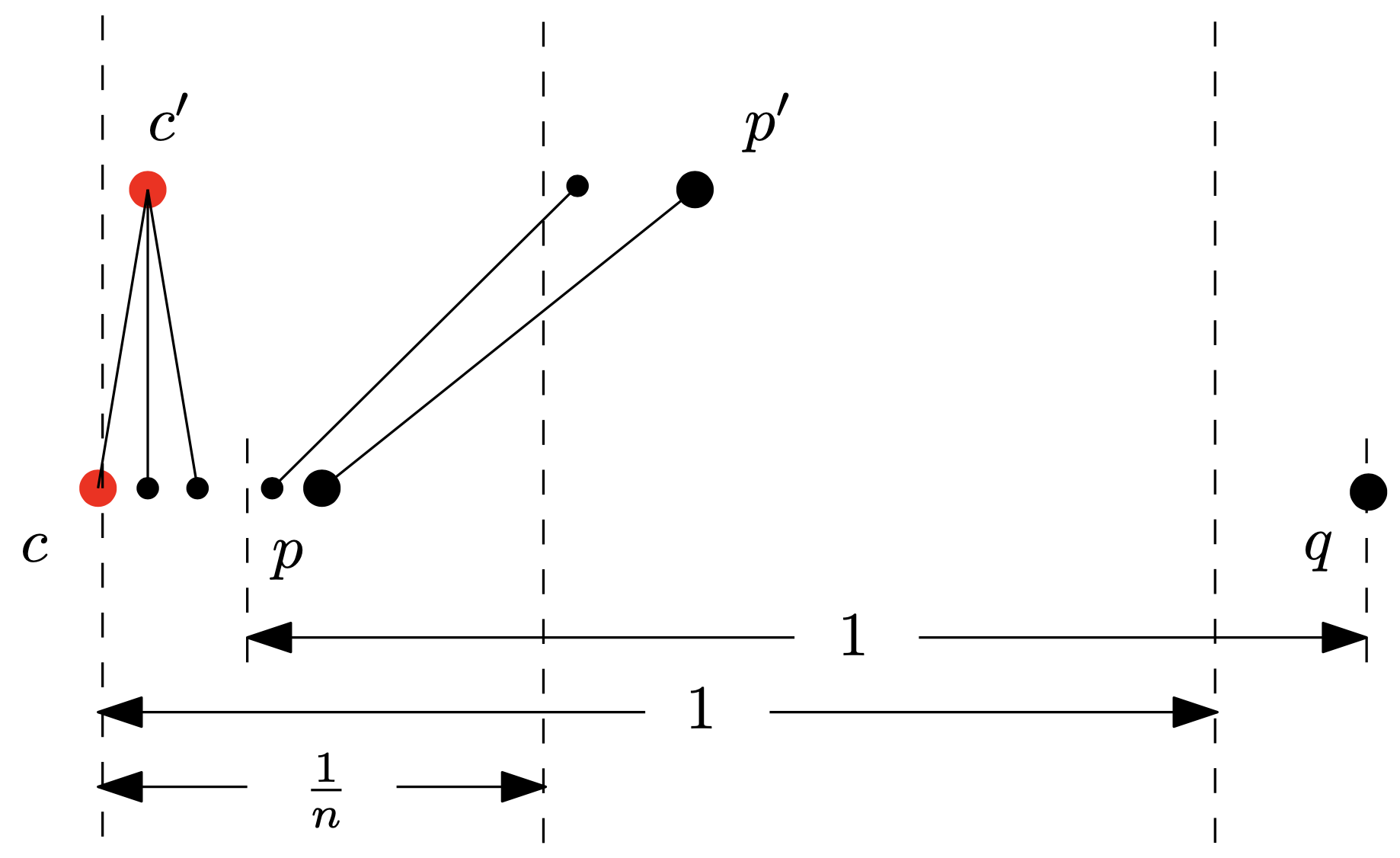
Udowodnijmy, że w każdych dwóch kolejnych ruchach czapeczka przesuwa się łącznie o co najmniej \(\frac{1}{n^2}.\) Niech \(c\) oznacza pozycję pchły z czapeczką, \(k\) – liczbę pcheł w zasięgu jej wzroku, \(p\) – najdalszą z tych pcheł, a \(c',\) \(p',\) odpowiednio, pozycje \(c\) i \(p\) po skoku. Przypuśćmy, że po pierwszym kroku pchła z pozycji \(c\) (teraz w \(c'\)) nadal zachowała czapeczkę i co więcej – przemieściła się o mniej niż \(\frac{1}{n^2}\) (jeśli któryś z tych warunków nie zachodzi, to już koniec dowodu). Mamy zatem: \[c+\frac{1}{n^2} > c' \geq \frac{1}{k}\left((k-1)c+p\right)= c-\frac{c}{k}+\frac{p}{k},\] czyli \[p<c+\frac{k}{n^2}\leq c+\frac{1}{n}\] (wszystkie sąsiadki \(c\) są ,,bardzo, bardzo blisko”). Ponieważ nie doszło do uziemienia, to \(p\) musiała widzieć \(\ell> k\) pcheł, w szczególności co najmniej jedną pchłę po swojej prawej; niech \(q\) będzie pierwszą z nich. Skoro jednak \(c\) nie widzi \(q,\) to \[c+1<q\leq p+1.\]
Wobec tego możemy oszacować pozycję \(p'\): \[p'\geq \frac{1}{\ell}\left((\ell-1)c+q\right) > \frac{1}{\ell}\left((\ell-1)c+c+1\right)=c+\frac{1}{\ell}\geq c+\frac{1}{n}\] (\(q\) odciąga \(p\) ,,trochę w prawo”) oraz, jak już wiemy: \[p'\leq p+\left(1-\frac{1}{n}\right)<c+\frac{1}{n}+1-\frac{1}{n}=c+1<c'+1.\]
Powiedzmy, że \(c'\) widzi po pierwszym skoku \(k'\) pcheł. Nasze obliczenia pokazują, że \(p'\) jest jedną z nich. Zatem po drugim skoku: \[c'' \geq \frac{1}{k'}\left((k'-1)c'+p'\right)> \frac{1}{k'}\left((k'-1)c+c+\frac{1}{n}\right) = c+\frac{1}{nk'} \geq c+\frac{1}{n^2},\] a więc faktycznie po dwóch skokach czapeczka przebyła co najmniej dystans \(\frac{1}{n^2}\) (,,wyraźnie dalej”). Hop, hop.
Rys. 3. Ilustracja dowodu
Reasumując, jeżeli początkowa odległość skrajnych pcheł wynosi \(d,\) a czapeczka w każdych dwóch ruchach przesuwa się łącznie o co najmniej \(\frac{1}{n^2},\) to liczba ruchów, w których coś się zmienia, wynosi co najwyżej \(2dn^2,\) a dalej stan jest już stabilny. W rzeczywistości pokazaliśmy nawet więcej: możemy bez straty ogólności założyć, że \(d\leq n\) (inaczej mamy rozpad na niezależne podproblemy), zatem pchły osiągają stan stabilny po co najwyżej \(2n^3\) iteracjach, niezależnie od początkowych pozycji.
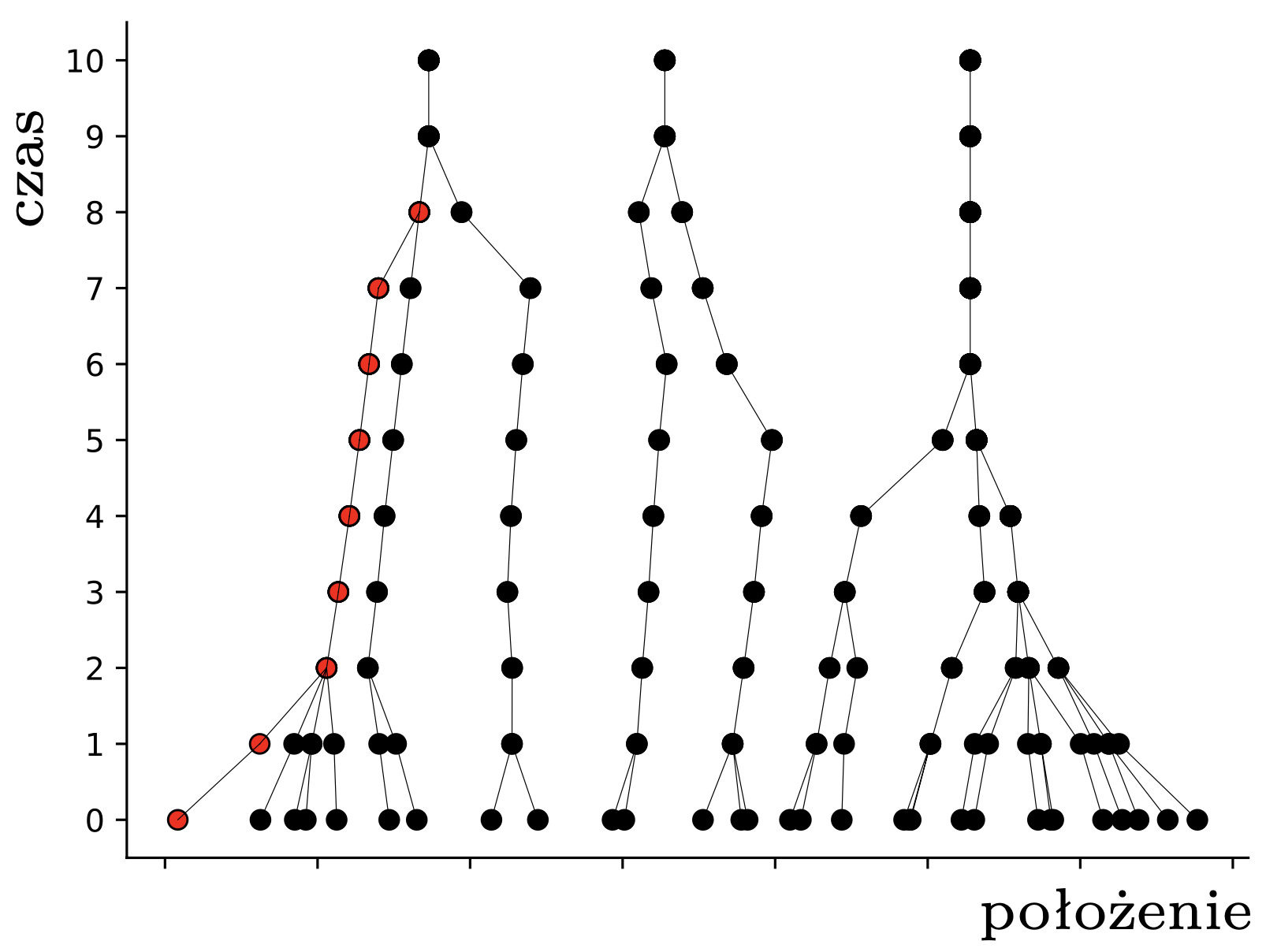
Powstaje naturalne pytanie, czy są układy \(n\) pcheł, które stabilizują się dopiero po liczbie kroków rzędu \(n^3.\) Odpowiedź brzmi: prawdopodobnie nie. Pchły rozpoczynające w punktach \(\{1,2,\ldots,n\}\) osiągają stabilność po około \(\frac{5}{6}n\) iteracji (rys. 4), co pozostawiamy jako żmudne ćwiczenie; można zajrzeć do [2]. W pracy [3] autorom udało się skomplikować ten przykład tak, że do stabilności potrzeba liczby kroków rzędu aż \(n^2.\) Jak dotąd nikomu nie udało się poprawić ani dolnego, ani, co bardziej zaskakujące, górnego oszacowania, choć wydaje się, że pchły mają więcej ,,luzu”, niż to uwzględnia nasza analiza z czapeczką, i można by to jakoś wykorzystać. Może ktoś z Czytelników podejmie się tego zadania? Można też zainteresować się innymi pytaniami, na przykład, jak przebiega i jak się statystycznie kończy ewolucja układu \(n\) pcheł umieszczonych losowo w przedziale długości \(d\)? Albo do jakiego stopnia pchła może w trakcie zabawy zmieniać kierunek, w którym skacze?
Rys. 4. Trajektorie pcheł startujących z punktów \(1,\ldots,20\)
Pozostawiając Czytelnika ze skaczącymi pchłami, uprzejmie donoszę, że ostatnio dzieci namówiły mnie na kisiel i po tym doświadczeniu podniosłem mu ocenę z \(0\) do \(0{,}001.\) Czekam na kolejny ruch. Hop!
Literatura
[1] A. Bhattacharya, M. Braverman, B. Chazelle and H. L. Nguyen, ,,On the convergence of the Hegselmann-Krause system”, Proceedings of the 4th Innovations in Theoretical Computer Science Conference (ICTS 2013), Berkeley CA, January 2013., https://arxiv.org/abs/1211.1909
[2] P. Hegarty and E. Wedin, ,,The Hegselmann-Krause dynamics for equally spaced agents”, Journal of difference equations and applications, vol. 22, no. 11, pp. 1621–1645, https://arxiv.org/abs/1406.0819
[3] P. Hegarty and E. Wedin, 2015. ,,A quadratic lower bound for the convergence rate in the one-dimensional Hegselmann–Krause bounded confidence dynamics”, Discrete & Computational Geometry, 53, pp.478-486., https://arxiv.org/abs/1406.0769