Klub 44

Oba warianty – odpowiedź tak. W podanych niżej przykładach przyjmujemy punkt \(C\) za środek ustalonego okręgu \(\Omega\) (o dowolnym promieniu), na którym umieszczamy pozostałe cztery punkty:
(a) punkty \(P,A,B,Q\) leżą na okręgu \(\Omega\) w tym porządku, w odległościach kątowych \({\measuredangle{PCA}=\measuredangle{ACB}=\measuredangle{BCQ}=30^\circ}\);
(b) punkty \(P,B,A,Q\) leżą na okręgu \(\Omega\) w tym porządku, w odległościach kątowych \({\measuredangle{PCB}=\measuredangle{ACQ}=60^\circ},\) \({\measuredangle{BCA}=150^\circ}.\)

Czytelnikom zostawiamy przyjemność naszkicowania tych układów i przekonania się, że wskazane konfiguracje faktycznie spełniają postawione warunki.

[Ciekawostka: są to (w obu przypadkach) jedyne takie konfiguracje, z dokładnością do podobieństwa oraz cyklicznej permutacji symboli \(A,B,C\)].

Autor zadania, Piotr Kumor, proponuje rozwiązanie dla \({r=4}\) z użyciem liczb Fermata \({F_n=2^{2^n}+1}\) (\({n=0,1,2,\ldots}\)). Zaczniemy więc od przypomnienia niektórych ich własności (zapewne znanych Czytelnikom; krótkie uzasadnienia – dla kompletności):

1. \({F_n=2+F_0F_1{\ldots}F_{n-1}}\)    (banalna indukcja).

2. Liczby \(F_n\) są parami względnie pierwsze (wniosek z W1).

3. Żadna z liczb \(F_n\) nie jest potęgą liczby naturalnej o wykładniku większym od 1.

Uzasadnienie W3: przypuśćmy, że \({F_n=a^t}\) (\({t>1}\)); jasne, że \(t\) nie może być potęgą dwójki, więc ma dzielnik nieparzysty \(s\); liczba \({2^{2^n}=a^t-1}\) dzieli się przez \({a^s-1=(a-1)(a^{s-1}+\ldots+a+1)}\); to jednak niemożliwe, bo suma w drugim nawiasie jest nieparzysta.

Właściwe rozwiązanie opiera się na spostrzeżeniu, że aby uzyskać tezę dla \({r=4},\) wystarczy wykazać, że dla nieskończenie wielu wykładników \(w\) można znaleźć różne liczby pierwsze \(p_1,p_2,p_3,p_4\) spełniające warunki: \[w\mid p_i-1,\ \ \ p_i\mid 2^w-1\ \ \ \hbox{dla}\;\;i=1,2,3,4. \ \ \ (*)\] To faktycznie wystarczy, bowiem wówczas każda z liczb \({2^{p_1-1}-1,\ldots,2^{p_4-1}-1}\) dzieli się przez \({2^w-1},\) więc też przez każdą z liczb \({p_1,\ldots,p_4},\) więc i przez ich iloczyn.

Przydatna będzie kolejna, mniej banalna, własność liczb Fermata:

1. Jeśli \({p\mid{F_n}}\) (\(p\) – liczba pierwsza; \({n\ge2}\)), to \({2^{n+2}\mid{p-1}}.\)

Dowód.  Niech \(\delta_n\) będzie najmniejszym wykładnikiem (\({{}>1}\)), dla którego \({2^{\delta_n}\equiv1} \text{ (mod } p).\) Ponieważ \({2^{2^n}\equiv-1},\) zatem \({2^{2^{n+1}}\equiv1},\) co pokazuje, że \({\delta_n=2^{n+1}}.\) Także \({2^{p-1}\equiv1}\) (małe tw. Fermata), więc \({\delta_n\mid{p-1}},\) czyli \({2^{n+1}\mid{p-1}}.\) Skoro \({n\ge2},\) liczba \(p\) ma postać \({p=8m+1}\) (dla pewnego naturalnego \(m\)). Ma więc miejsce przystawanie (mod \(p\)): \[\begin{aligned} (4m)!&=\textstyle\prod\limits_{k=1}^{2m}(2k)(1-2k)\equiv\\&\textstyle\equiv\prod\limits_{k=1}^{2m}(2k)(8m+2-2k)=\prod\limits_{k=1}^{4m}(2k)=2^{4m}(4m)! \end{aligned}\] Uzyskaną kongruencję wolno podzielić przez \((4m)!\) (\({{\perp{p}}}\)), otrzymując \({2^{4m}\equiv1}.\) Tak więc \({\delta_n\mid{4m}},\) czyli \({2^{n+1}\mid{4m}},\) skąd \({2^{n+2}\mid{8m}}.\) To kończy dowód własności W4 (znanej pod nazwą twierdzenie Lucasa).

Niech teraz \(n\) będzie taką liczbą naturalną, że \(F_n\) i \(F_{n+1}\) są liczbami złożonymi. Z własności W2 i W3 wynika, że iloczyn \(F_nF_{n+1}\) ma co najmniej cztery różne dzielniki pierwsze \(p_1,p_2,p_3,p_4.\) Na mocy własności W4 każda z liczb \({p_i-1}\) dzieli się przez \(2^{n+2}.\) Biorąc \({w=2^{n+2}},\) mamy (dla \({i=1,2,3,4}\)) pierwszą podzielność \((*).\) Druga też zachodzi, bowiem \({2^w-1=F_{n+2}-2=F_0F_1\ldots\, F_{n+1}}\) (własność W1), a ten iloczyn dzieli się przez \(F_nF_{n+1},\) więc i przez te cztery liczby pierwsze. (Warto zauważyć, że są one większe niż \(2^{n+2}\)).

Jeżeli istnieje nieskończenie wiele liczb \(n,\) dla których \(F_n\) i \(F_{n+1}\) są liczbami złożonymi, to – zgodnie z akapitem otaczającym warunki \((*)\) – dostajemy obiecaną tezę dla \({r=4}.\)

Jednak nikt nie wie, czy jest nieskończenie wiele takich par. Przyjmijmy więc, że nie; czyli że istnieje taka liczba \(M,\) że dla każdego \({n>M}\) co najmniej jedna z liczb \(F_n,\) \(F_{n+1}\) jest liczbą pierwszą. Można przyjąć, że \({M\ge3},\) wtedy \({2^n\ge{n+9}}\) dla \({n>M}.\) Ustalmy taki numer \(n.\) Wśród dziewięciu liczb \({F_n,\ldots,F_{n+8}}\) są co najmniej cztery liczby pierwsze \(p_1,p_2,p_3,p_4.\) Ponownie sprawdzimy warunek \((*),\) biorąc tym razem \({w=2^{n+9}}.\) Każda z czterech liczb \(p_i\) jest pewną liczbą \(F_{n+j}\) (\({0\le{j}\le8}\)), zatem \({p_i-1=2^{2^{n+j}}}\) dzieli się przez \(2^{n+9},\) czyli przez \(w.\)

To pierwsza podzielność \((*).\) Drugą uzasadniamy podobnie jak poprzednio: \({2^w-1=F_{n+9}-2=F_0F_1{\ldots}F_{n+8}}\) (własność W1), a ten iloczyn dzieli się przez te cztery liczby pierwsze. Mogą one być dowolnie wielkie, skoro \(M\) może być dowolnie wielkie.

To ostatecznie kończy dowód tezy dla \({r=4}\): istnieją czwórki dowolnie wielkich liczb pierwszych o wymaganych w zadaniu własnościach.

Klocek będzie pływał w stanie równowagi trwałej, gdy po obróceniu go o niewielki kąt \(\alpha\) (rys. 1) wypadkowy moment sił będzie powodował jego powrót do położenia równowagi.

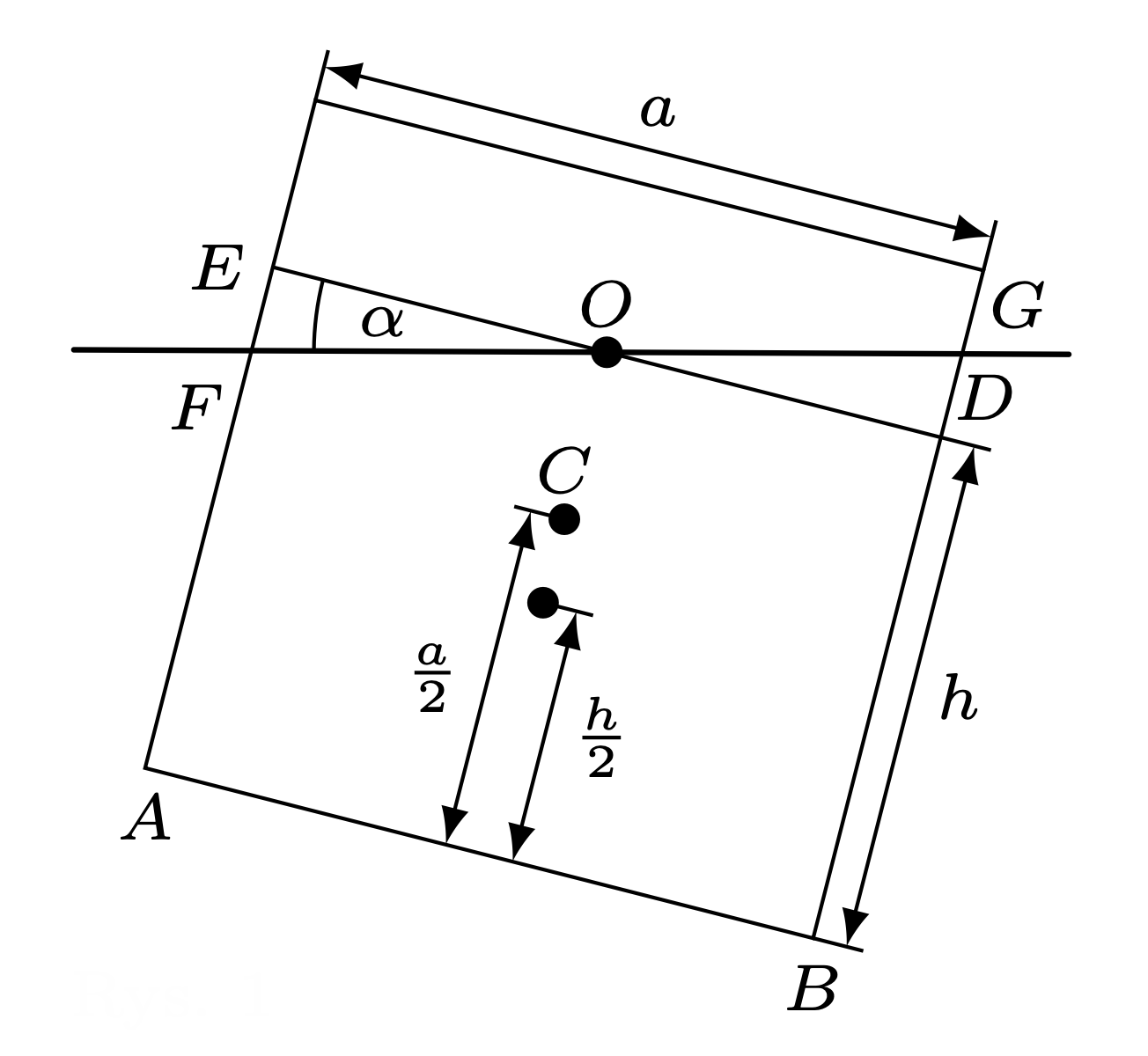
Rys. 1

Wygodnie jest liczyć momenty sił względem podłużnej osi klocka przechodzącej przez środek jego przekroju poprzecznego \(C\) (rys. 1), bo względem tej osi moment siły ciężkości wynosi zero.

Moment siły wyporu działającej na część klocka zanurzoną w wodzie jest równy \[M=M_{OGD}-(M_{ABDE}-M_{OEF}).\] Oznaczając: \(M_{OGD}=M_{OEF}=M_2,\) \(M_{ABDE}=M_1,\) możemy zapisać warunek na trwałość równowagi pływającego klocka: \[\tag{1} \label{GrindEQ__1_a} M>0 \ \Rightarrow \ 2M_2>M_1.\] Oznaczając długość klocka przez \(L,\) a gęstość wody przez \(\rho ,\) mamy: \[\tag{2} \label{GrindEQ__2_a} \hbox{$M_1=\rho gLahl_1,$ gdzie $l_1=\left({a}/{2}-{h}/{2}\right)\sin \alpha \approx \left({a}/{2}-{h}/{2}\right)\alpha ,$}\] \[\tag{3}\label{GrindEQ__3_a} \text{$M_2=\rho gLa^2{\rm{tg}\,}\alpha {l_2}/{8\approx \rho gL{a^2\alpha l_2}/{8}},$ gdzie $l_2\approx {2a}/{6}+\left(h-{a}/{2}\right)\alpha .$}\] Głębokość \(h\) zanurzenia klocka w stanie równowagi znajdujemy z warunku \[\text{$\rho ahL={\rho }_xa^2L,$ gdzie ${\rho }_x$ jest gęstością klocka.}\] Po podstawieniu \(\eqref{GrindEQ__2_a}\) i \(\eqref{GrindEQ__3_a}\) do \(\eqref{GrindEQ__1_a}\) i wprowadzeniu oznaczenia \({{\rho }_x}/{\rho }=x\) dostajemy: \[x^2-\left(1-{\alpha }/{2}\right)x+{\left(2-3\alpha \right)}/{12}>0.\] Uwzględniając, że \(\alpha\) jest małe, a \(\rho =1\) g/cm\(^3\), otrzymujemy warunki na gęstość klocka: \[\text{$0<{\rho }_x<0{,}21\ \rm{g}/{{cm}^3}$ lub $0{,}79\ {\rm{g}/{cm}}^3<\rho _x<1\ \rm g/cm^3.$}\]

Aby w gumowej taśmie mogła rozchodzić się sprężysta fala poprzeczna, taśma musi być naciągnięta. W naszym zadaniu siła naciągu taśmy wywołana jest przez jej ruch obrotowy.

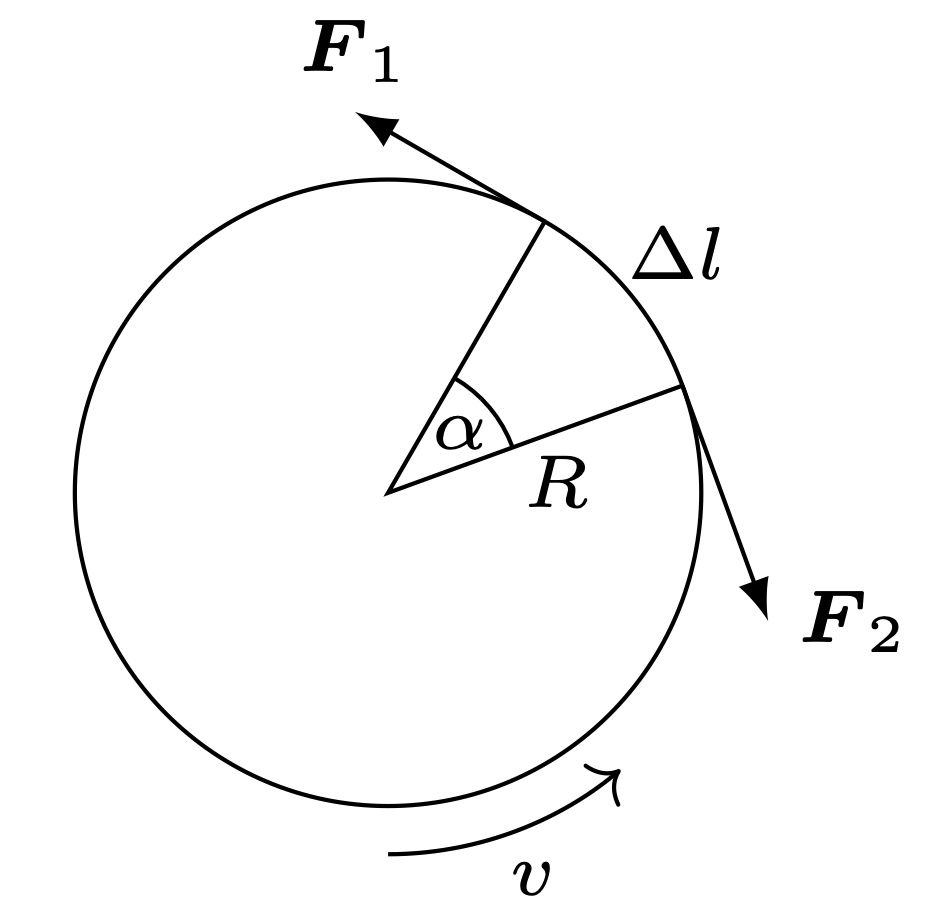
Rys. 2

Rozważmy mały element taśmy o długości \(\Delta l=R\alpha\) i masie \(\Delta m=\rho S\Delta l\) (rys. 2), gdzie \(\rho\) jest jego gęstością a \(S\) polem przekroju poprzecznego. Działają na niego sąsiednie elementy siłami \({\boldsymbol{F}}_1\) i \({\boldsymbol{F}}_2,\) stycznymi do taśmy. Wartość \(F\) tych sił jest szukanym naciągiem taśmy, a ich wypadkowa nadaje rozważanemu elementowi przyspieszenie dośrodkowe \({v^2}/{R}.\) Zgodnie z drugą zasadą dynamiki \[F\alpha =\rho SR\alpha {v^2}/{R},\] stąd \[\tag{4} \label{GrindEQ__1_} F=\rho Sv^2 .\] Szukana prędkość fali jest taka sama jak w przypadku prostoliniowej taśmy, której naciąg \(F\) został uzyskany za pomocą sił zewnętrznych.

W inercjalnym układzie odniesienia poruszającym się wzdłuż taśmy z prędkością fali \(u\) fala jest nieruchomą sinusoidą, a taśma ślizga się wzdłuż tej sinusoidy w kierunku przeciwnym do kierunku rozchodzenia się fali. Fragment trajektorii małego odcinka taśmy w pobliżu wierzchołka sinusoidy można przybliżyć przez łuk okręgu o promieniu \(r\) oparty na kącie \(\varphi .\) Ponieważ amplituda drgań jest mała, możemy napisać: \[\tag{5} \label{GrindEQ__2_} \text{$F\varphi =\rho Sr\varphi {u^2}/{r},$ stąd $u^2={F}/{\rho S}.$}\] Podstawiając wartość \(F\) z \(\eqref{GrindEQ__1_}\), otrzymujemy, że prędkość rozchodzenia się fali względem pierścienia równa jest prędkości obrotu pierścienia: \(u=v.\)