Afiliacja: Nauczyciel fizyki i matematyki w 42 Autorskim LO w Warszawie
Po przeczytaniu tytułu Czytelnik może pomyśleć, że Delta zaczęła publikować opowiadania fantastyczne spod znaku historii alternatywnej. Oto w połowie XX wieku gdzieś w Królestwie Galicji i Lodomerii, żyjącym pod łaskawym panowaniem Franciszka Józefa II, napędzana gorlicką ropą rakieta wzbija się na Księżyc… Nic z tych rzeczy! Wspomniany specjalista żył naprawdę. Urodził się w austrowęgierskim wówczas Siedmiogrodzie, w rodzinie mówiącej w domu po niemiecku, a nazywał się Hermann Oberth. Gdy skończył fizykę w Heidelbergu, wrócił do Siedmiogrodu i podjął pracę jako profesor gimnazjum. Prowadził jednak także teoretyczne badania nad pojazdami kosmicznymi, a napisana na podstawie jego rozprawy naukowej o fizyce lotów rakietowych książka popularnonaukowa wywołała wśród młodych Niemców prawdziwą modę na kosmonautykę. Do założonego na fali tej mody „Towarzystwa na rzecz Podróży Statkami Kosmicznymi”** należał także Wernher von Braun, niemiecki konstruktor rakiet, po II Wojnie Światowej współtwórca amerykańskiego programu kosmicznego.
**Początkowo sąd odmówił rejestracji Verein für Raumschiffahrt (Towarzystwa Podróży Kosmicznych), twierdząc, że nie ma takiego słowa, jak Raumschiffahrt. To dziwne, wydawałoby się, że po niemiecku wystarczy zapisać kilka słów bez spacji, a nowy wyraz pojawia się automatycznie.
Jak to zwykle bywa w historii, skutki pracy Obertha były i pozytywne, i negatywne – być może bez niego nie mielibyśmy lądowania na Księżycu, ale także i hitlerowskich rakiet V1 i V2.
Efekt Obertha.
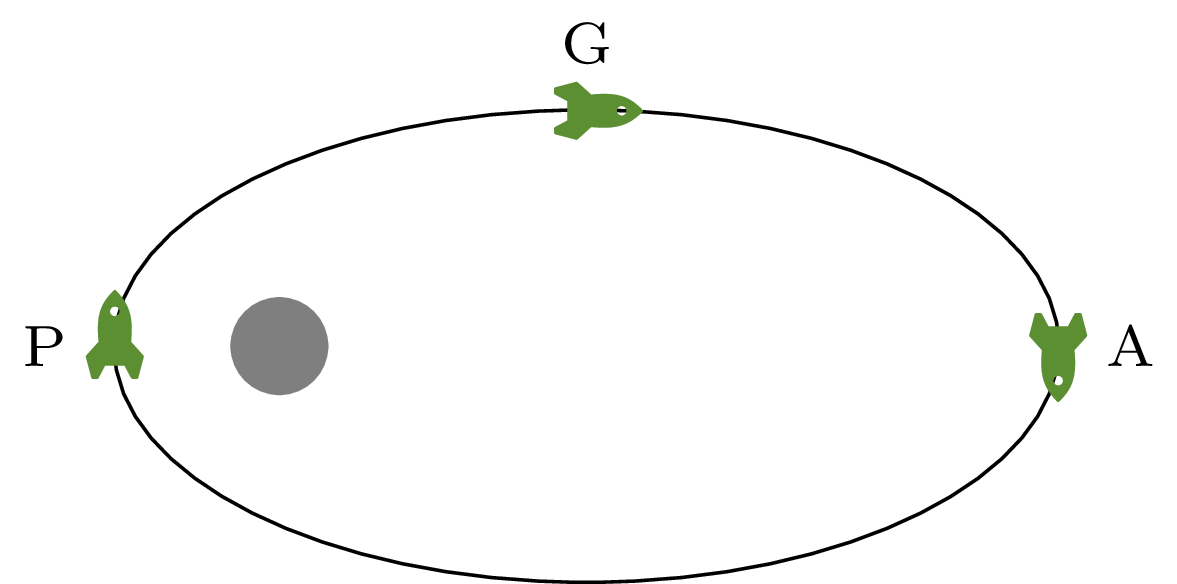
Uczony dziś znany jest przede wszystkim z „efektu Obertha”. Na czym ów efekt polega? Wyobraźmy sobie statek kosmiczny krążący wokół planety po eliptycznej orbicie. Jego załoga chce opuścić orbitę i w związku z tym potrzebuje uzyskać jak największą prędkość, ale na manewr może przeznaczyć tylko określoną ilość paliwa. W którym miejscu orbity włączyć silnik: w apocentrum (A), w perycentrum (P) czy gdzieś pośrodku (G)? A może to wszystko jedno?
Zakładamy, że silnik pracuje bardzo krótko (w skali rysunku rakieta jest ciągle w tym samym miejscu), ale za to z dużą mocą. Proponuję w tym momencie przerwać czytanie i zastanowić się samemu.
Cztery odpowiedzi.
A oto odpowiedzi czterech współziomków Obertha.
Hans
To wszystko jedno. Zgodnie z drugą zasadą dynamiki przyrost pędu jest w każdym wypadku taki sam (\(\Delta p=F\Delta t\)), więc także prędkość wzrośnie o tyle samo.
Jancsi
Najlepiej włączyć silnik w apocentrum. Co prawda włączenie silnika zawsze doda tyle samo energii, ale żeby wyrwać się z punktu A, potrzeba mniej energii niż z punktu P.
Růžena
Najlepiej włączyć silnik w punkcie G, ale nie po prostu „gdzieś”, tylko w połowie drogi między apocentrum i perycentrum. Wtedy rakieta poleci bardziej w stronę „od planety”, a nie w bok, więc szybciej się oddali i nie zdąży stracić tyle energii.
Oleńka
Najlepiej włączyć silnik w punkcie P. Siła ciągu będzie ta sama, będzie działać przez ten sam czas, ale w tym czasie rakieta przebędzie największą drogę, a w takim razie wykonana praca będzie największa (\(W=Fs\)) i rakieta zyska najwięcej energii.
Kto ma rację i dlaczego inni jej nie mają?
Proponuję znowu się zatrzymać i pomyśleć. A potem obalimy po kolei wszystkie podane argumenty.
Hans
Owszem, prędkość wzrośnie za każdym razem o tyle samo, ale jednakowy przyrost prędkości nie oznacza jednakowego przyrostu energii. We wzorze na energię kinetyczną prędkość występuje w kwadracie. Jeśli zwiększymy prędkość z 1 km/s do 2 km/s, energia kinetyczna wzrośnie o \(2^2-1^2 = 3\) jednostki umowne,
a jeśli zwiększymy ją z 5 km/s do 6 km/s, to wzrośnie aż o \(6^2- 5^2 = 11\) takich jednostek. A do wyrwania się z pola grawitacyjnego planety potrzebna jest odpowiednia energia.
Jednostki równe ½\({} \cdot{}\)(masa rakiety)\({} \cdot{}\)(km/s)\(^2\)
Jancsi
Do oddalenia się od planety z punktu A rzeczywiście jest potrzebna mniejsza energia niż z punktu P. Ale tę różnicę dokładnie kompensuje różnica energii kinetycznych między tymi punktami. A poza tym skąd wiemy, że silnik dostarczy tyle samo energii?
Růžena
Dlaczego „nie zdąży”? Ubytek energii kinetycznej zależy od przyrostu energii potencjalnej, a nie od czasu. Jeśli rakieta będzie się szybciej oddalać (będzie miała większą prędkość radialną), to po prostu będzie szybciej traciła energię.
Oleńka
Przyrost energii kinetycznej rakiety jest równy energii chemicznej paliwa spalonego przez rakietę. Skąd miałaby się wziąć dodatkowa energia?
To kto ma rację, skoro nikt jej nie ma?
Zdradźmy od razu, że jako patriota nie mogłem rozdzielić ról inaczej: rację ma Oleńka. Jej argument ze wzorem definicyjnym pracy jest w pełni poprawny. Ale jak odpowiedzieć na pytanie, skąd się wzięła dodatkowa energia? Otóż pierwsze zdanie mające zbić argumenty Oleńki nie jest prawdziwe. Należałoby powiedzieć: Przyrost energii kinetycznej rakiety i gazów wylotowych jest równy energii chemicznej paliwa spalonego przez rakietę. Tymczasem, gdy rakieta leci szybciej, jej gazy mają mniejszą prędkość w zewnętrznym układzie odniesienia. Więcej energii zostaje więc dla rakiety.
A w układzie odniesienia rakiety? W nim rakieta w ogóle się nie porusza, porusza się natomiast planeta, a do tego nasz układ nie jest inercjalny. Analiza będzie więc dużo bardziej skomplikowana.
A co do Oleńki – jak pisał już Sienkiewicz – to białogłowy z tak grzecznym umysłem drugiej nie znaleźć. Kogo zaś takowe polityczne argumentum ad rationem nie przywoła, dla tego cytatę mamy przystojniejszą: Ślepy! Głupi warchole! Nie byłoż ci posłuchać Oleńki!