Wyznaczyć wszystkie trójki \((a, b, c)\) dodatnich liczb całkowitych, dla których \(a+bc,\) \(b+ac,\) \(c+ab\) są liczbami pierwszymi i wszystkie dzielą liczbę \((a^2+1)(b^2+1)(c^2+1).\)
Zauważmy, że gdyby liczby pierwsze \(a+bc,\) \(b+ac,\) \(c+ab\) były parami różne, to ich iloczyn dzieliłby \((a^2+1)(b^2+1)(c^2+1),\) więc w szczególności zachodziłaby nierówność: \[\begin{split} (bc+a)(ca+b)(ab+c) &\le \\ &\le (a^2+1)(b^2+1)(c^2+1), \end{split}\] równoważna następującej: \[(abc-1)(a^2+b^2+c^2+1) \le 0.\] Oczywiście ostatnia nierówność nie może zajść poza przypadkiem trójki \((a,b,c)=(1,1,1),\) która spełnia warunki zadania.
Wobec tego dwie z danych liczb pierwszych są równe, bez straty ogólności załóżmy, że \(a+bc=b+ac.\) Po przekształceniach mamy \((a-b)(c-1)=0,\) czyli \(a=b\) lub \(c=1.\)
Jeśli \(a=b,\) to skoro \(a+bc=a(c+1)\) jest liczbą pierwszą, to \(a=b=1.\) Jednakże wtedy \(c+1\) jest liczbą pierwszą i dzieli \(4(c^2+1)=4(c-1)(c+1)+8.\) Jest to możliwe wtedy, gdy \(c+1\) dzieli \(8,\) a więc gdy \(c=1.\) Ponownie otrzymaliśmy trójkę \((1,1,1).\)
Rozpatrzmy przypadek \(c=1\) i przypuśćmy, że któraś z liczb \(a,b\) jest większa od 1. Wówczas \(ab+1,\) \(a+b\) są liczbami pierwszymi większymi od \(2,\) które dzielą \(2(a^2+1)(b^2+1),\) zatem dzielą też \((a^2+1)(b^2+1).\) Bez szkody dla ogólności załóżmy, że \(a<b,\) wtedy \(ab+1>a^2+1,\) więc \(ab+1 \mid b^2+1,\) skąd \(ab+1 \mid b^2+1-(ab+1)=b(b-a).\) Jednakże liczby \(b,\) \((b-a)\) są dodatnie i mniejsze od \(ab+1\) – sprzeczność.
W zbiorze \(\mathcal{S}\) zawierającym \(n\) elementów wybrano \(\lfloor\sqrt{2n}\rfloor+2\) podzbiorów tak, że suma dowolnych trzech z nich jest równa \(\mathcal{S}.\) Udowodnić, że suma pewnych dwóch z nich jest równa \(\mathcal{S}.\)
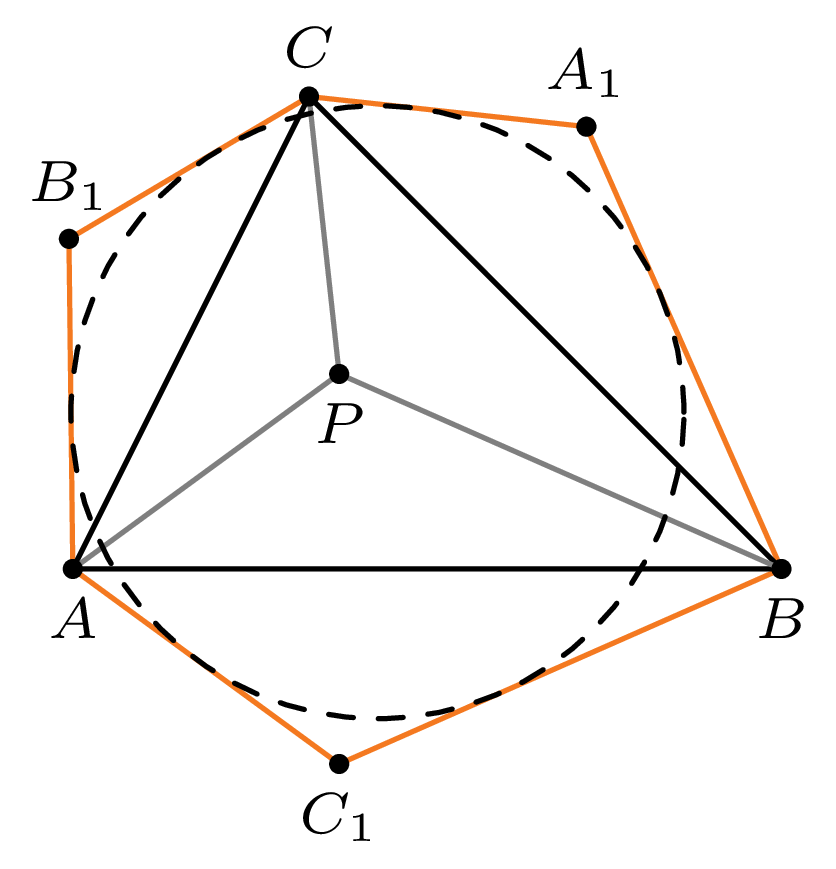
Punkt \(P\) leży wewnątrz trójkąta ostrokątnego \(ABC.\) Niech \(A_1,\) \(B_1,\) \(C_1\) będą punktami symetrycznymi do \(P\) względem prostych \(BC,\) \(CA\) i \(AB.\) Załóżmy, że w sześciokąt \(AB_1CA_1BC_1\) można wpisać okrąg. Udowodnić, że \[\measuredangle BPC=\measuredangle CPA=\measuredangle APB.\]

Niech \(\Omega\) będzie okręgiem wpisanym w dany sześciokąt oraz niech \(X\) i \(Y\) będą punktami styczności tego okręgu odpowiednio z odcinkami \(AB_1\) oraz \(AC_1.\) Zauważmy, że \(AB_1 = AP= AC_1\) oraz \(AX=AY,\) stąd \[B_1X=AB_1-AX=AC_1-AY=C_1Y.\] Zatem trójkąty prostokątne \(OXB_1\) i \(OYC_1\) są przystające (bkb). Wobec tego, ponieważ \(B_1O\) i \(C_1O\) są dwusiecznymi kątów \(AB_1C\) i \(AC_1B,\) dostajemy \[\begin{split} \measuredangle APC&=\measuredangle AB_1 C=2\measuredangle XB_1O=\\ &=2\measuredangle YC_1O =\measuredangle AC_1 B=\\ &=\measuredangle APB. \end{split}\] Podobnie \(\measuredangle APC=\measuredangle BPC,\) skąd teza.
Do badania struktury kryształów, poza promieniowaniem rentgenowskim, stosuje się także wiązki elektronów. Obraz dyfrakcyjny pozwalający na ,,odczytywanie” struktury atomowej powstaje, gdy długość fali, \(\lambda,\) wiązki jest porównywalna ze stałymi sieci krystalicznej (odległościami sąsiadujących atomów). Oszacuj, jaki jest współczynnik załamania, \(n,\) wiązki elektronów na powierzchni metalu w badaniach struktury krystalicznej. Odległości międzyatomowe są rzędu kilku angstremów (kilka razy \(10^{-10}\) m), masa elektronu \(m_e = 9{,}1\cdot 10^{-31}\) kg, wartość ładunku elektronu \(e = 1{,}6\cdot 10^{-19}\) C, stała Plancka \(h = 6{,}63\cdot 10^{-34}\) Js, a typowa praca wyjścia dla metali \(W \approx 5\) eV.
W obliczaniu pędu elektronu nie uwzględnialiśmy poprawek relatywistycznych, co uzasadnia otrzymana wartość \(e\cdot U = 151\) eV, która jest pomijalnie mała w porównaniu z masą spoczynkową elektronu, \({m_ec^2 = 511}\) keV. Średni potencjał wewnątrz metali ,,odczuwany” przez elektrony jest większy niż wynikający z pracy wyjścia i wynosi 10 V do 15 V, co prowadziłoby do wartości \(n \le 1{,}05\) V.
Wskaźnik laserowy emituje światło o długości fali \(\lambda = 650\) nm. Wiązkę wskaźnika skierowano na powierzchnię wody. Ile wynosi pęd \(p_w\) fotonów wiązki w wodzie? Współczynnik załamania wody \(n = 1,33,\) stała Plancka \({h = 6{,}63\cdot 10^{-34}}\) Js.