Afiliacja: Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Spłaszczacz Ziemi i Cassinich
(Wolter o Maupertuisie)
Pierre Louis Moreau de Maupertuis
(1698–1759)
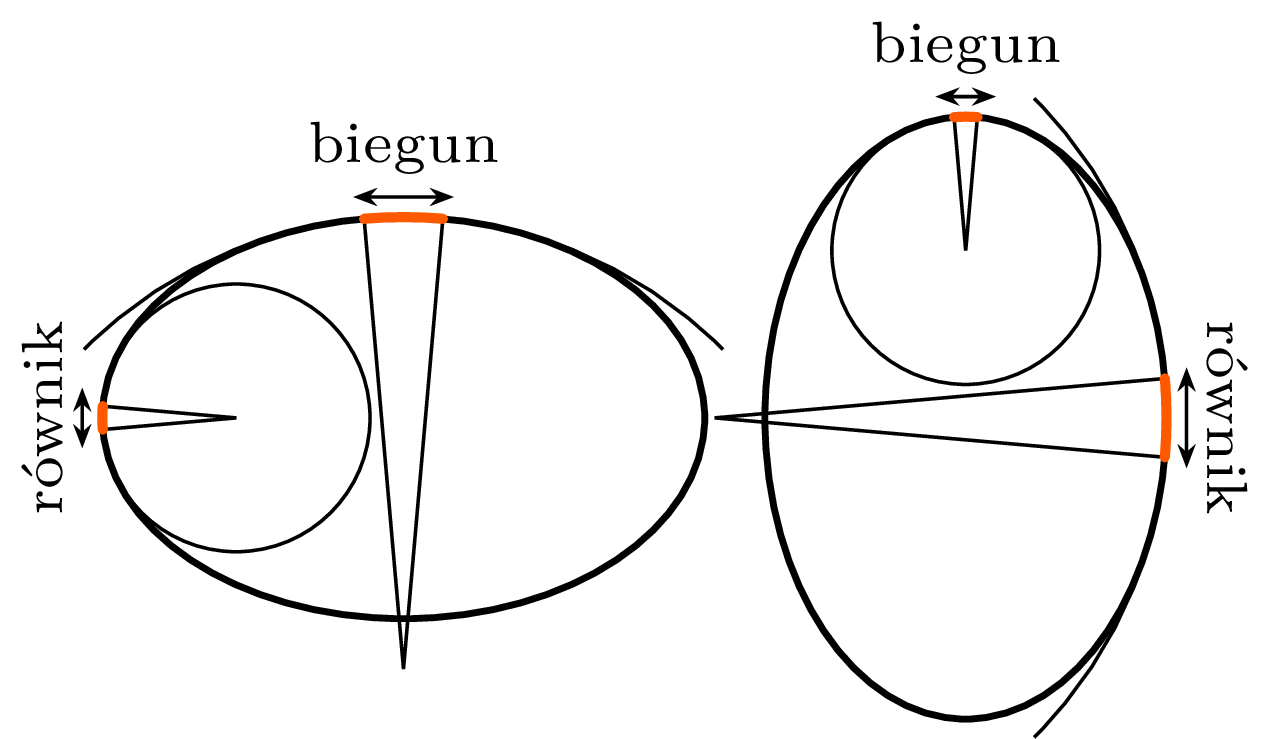
W trzeciej dekadzie XVIII wieku bardzo już nabrzmiał problem prawdziwego kształtu ,,globu ziemskiego”. W 1718 roku Jacques Cassini, dyrektor Obserwatorium Paryskiego, oznajmił, że Ziemia jest wydłużona na biegunach. Stwierdził to na podstawie wieloletnich pomiarów długości jednego stopnia południka – w Dunkierce na północy Francji i w Pirenejach, 800 mil na południe – które pokazywały, że długość jednego stopnia południka w Dunkierce jest krótsza o około 141 sążni od tej w Pirenejach (przed wprowadzeniem metra w 1791 roku odległość liczono między innymi sążniami: 1 sążeń = \(1{,}949\) m). Jego rozumowanie opierało się na obserwacji, że gdyby Ziemia była idealną kulą, wówczas długość jednego stopnia szerokości geograficznej byłaby taka sama niezależnie od miejsca pomiaru – uzyskana różnica świadczy więc o odmiennym kształcie Ziemi (zob. rysunek obok). Stanowisko Cassiniego podparł swoimi obliczeniami Johann Bernoulli w nagrodzonej przez Akademię Francuską pracy z 1734 roku. Wynikało z nich, że przy założeniu prawdziwości teorii wirów Kartezjusza tak właśnie powinno być.
Porównanie Ziemi spłaszczonej i wydłużonej na biegunach. Na obu rysunkach zaznaczono łuk południka odpowiadający jednemu stopniowi szerokości. Długość takiego łuku jest proporcjonalna do promienia krzywizny w danym punkcie, dlatego pomiary na biegunie i na równiku mogą się różnić
Z drugiej strony pomiary przeprowadzone w tak małej odległości między punktami (800 mil) nie były dostatecznie miarodajne, a zmierzona różnica długości jednego stopnia południka mieściła się w granicach błędu pomiarowego. Ponadto eksperyment z zegarem wahadłowym (wynalezionym przez Christiana Huygensa w 1657 roku) przeprowadzony już w 1671 roku przez Jeana Richera w Cayenne w Gujanie Francuskiej wykazał, że zegar spóźnia się o 2 minuty i 28 sekund na dobę w stosunku do czasu odmierzanego w Paryżu. Choć interpretacja tego wyniku nie była jasna, sam wynik był logicznie zgodny z zamieszczonymi w Principiach (1686) obliczeniami Newtona wykorzystującymi dane Richera i prowadzącymi do wniosku, że Ziemia jest spłaszczona na biegunach. Teorie i obliczenia Newtona dotyczące kształtu Ziemi zostały podjęte we wczesnych latach 30. XVIII wieku przez wielu uczonych, na czele z matematykami. Wszyscy też mogli zobaczyć, że Jowisz jest spłaszczony na biegunach. Świat naukowy oczekiwał więc szybkiego rozstrzygnięcia problemu kształtu Ziemi.
Pomiar odległości (w poziomie) między dwoma punktami wykonywano przy pomocy tyczek pomiarowych, jednak w nierównym terenie wymagało to dodatkowego użycia żerdzi
Rozłam w Akademii Francuskiej.
W Akademii Francuskiej powstał rozłam między zwolennikami kartezjańskiej teorii wirów i Ziemi wydłużonej na biegunach a zwolennikami newtonowskiej teorii grawitacji i Ziemi spłaszczonej na biegunach. Zwolenników teorii wirów bardzo aktywnie reprezentował wspomniany już wybitny astronom Jacques Cassini. Był on synem włoskiego astronoma Giana Domenico Cassiniego, sprowadzonego w 1669 roku przez Ludwika XIV do Francji, gdzie miał założyć Obserwatorium Paryskie. Jako jego dyrektor Gian Domenico Cassini kierował wieloma ważnymi projektami, a pierwszym wśród nich było stworzenie nowej, zaskakującej, mapy Francji, o której Ludwik XIV wyraził się w 1682 roku, że kosztowała go spory obszar jego królestwa. Następnie, na przełomie wieków, Gian Domenico i Jacques zainicjowali wielki projekt triangulacji Francji z północy na południe, wzdłuż południka, w celu obliczenia obwodu Ziemi i określenia jej kształtu. Jacques Cassini kontynuował ten projekt po śmierci ojca w 1712 roku. Jego obliczenia ogłoszone w 1718 roku nie wzbudzały zastrzeżeń przez 15 lat, dopóki we wczesnych latach 30. nie zostały zakwestionowane przez kilku matematyków.
Liderem zwolenników Newtona był młody i rzutki uczony Pierre Louis Moreau de Maupertuis, przyjęty do Akademii w 1723 roku (w wieku 25 lat), a pięć lat później do Towarzystwa Królewskiego w Londynie. Był on pierwszym badaczem we Francji, który zrozumiał i docenił prawa grawitacji Newtona. Jednym z jego największych osiągnięć było odkrycie, w latach 40., zasady najmniejszego działania, przypisywanej czasem Eulerowi, Lagrange’owi czy Hamiltonowi, którzy rozwinęli matematyczną stronę koncepcji Maupertuisa. Zasada ta jest w swojej istocie jednym z największych uogólnień we wszystkich naukach fizycznych, i tak rozumiał ją jej twórca. Poza matematyką i mechaniką zasadę Maupertuisa można odnaleźć w prawach: stabilności środowiska wewnętrznego Claude’a Bernarda, homeostazy Waltera B. Cannona, równowagi chemicznej Le Chateliera, równowagi w przyrodzie czy równowagi sił ekonomicznych. Ponadto Maupertuis jako pierwszy zastosował rachunek prawdopodobieństwa do badania dziedziczności, a odkryte fakty skłoniły go do opracowania teorii dziedziczności, która okazuje się zdumiewająco zgodna z dzisiejszą teorią genów [Glass, 1947, 1955].
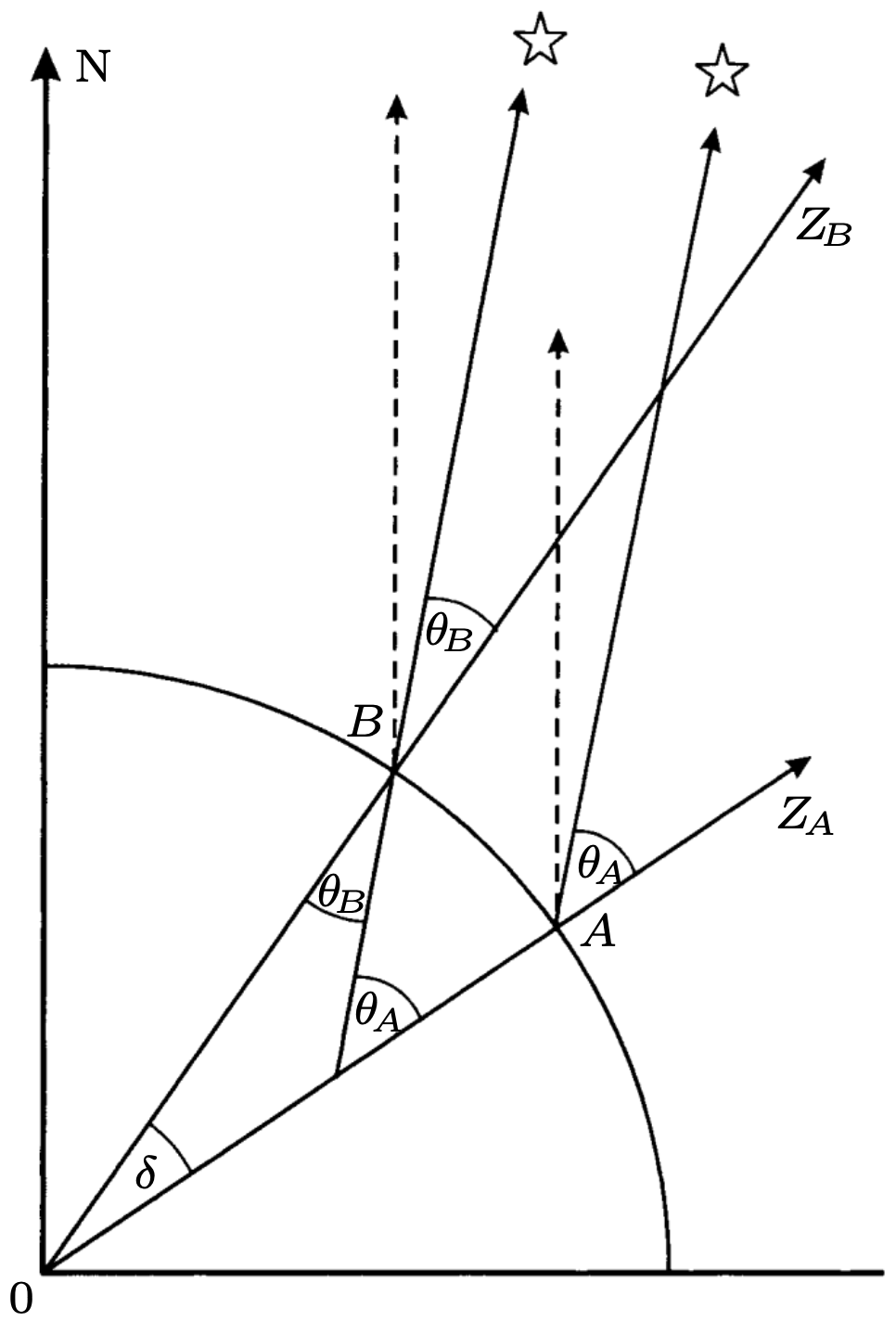
Metoda obliczenia długości południka odpowiadającego jednemu stopniowi. Jeśli odległość \(AB\) wzdłuż południka jest znana, to za odległość odpowiadającą jednemu stopniowi w tym obszarze przyjmujemy \(\frac{AB}{\theta_{\!A} - \theta_{\!B}}.\) Z obu miejsc \(A\) i \(B\) obserwujemy tę samą gwiazdę, a ze względu na dużą jej odległość linie wyprowadzone z tych punktów do gwiazdy przyjmujemy jako równoległe
W latach 30. XVIII wieku geodezja stawała się coraz bardziej matematyczna. Maupertuis i inni, uzbrojeni w subtelne metody matematyczne, takie jak rachunek różniczkowy i całkowy oraz geometria różniczkowa, pisali ze sceptycyzmem o metodach i obliczeniach Cassiniego. Na przykład Alexis Clairaut stwierdził, że obliczenia Cassiniego były zbyt proste, albowiem były oparte na geometrii sferycznej, podczas gdy geometria na sferoidzie jest bardziej złożona. Żądano precyzyjniejszych pomiarów, a dawne pomiary krytykowano. Proponowano też nowe metody obliczeń, oparte na przykład na pomiarach długości łuku równoleżników na różnych szerokościach geograficznych (na potrzeby porównania badamy wtedy łuki zawarte pomiędzy dwoma ustalonymi południkami).
Zarzutom wobec tradycyjnych metod w geodezji wtórował sam Wolter, mający cięte pióro i duży wpływ na opinię publiczną. Warto w tym miejscu przypomnieć, że Maupertuis i Wolter w latach 1726–1728 spędzili jakiś czas w Londynie, wymieniając poglądy z tamtejszymi uczonymi i nasiąkając głoszonymi przez nich ideami. Newton stawał się coraz bardziej popularny w Paryżu, szczególnie wśród młodszego pokolenia, ale dla wielu ze starej kadry był solą w oku. Problem kształtu Ziemi dobrze wpisywał się w retorykę obrony honoru nauki francuskiej, ugruntowanej wieloletnimi pomiarami i przemawiającą do wyobraźni teorią Kartezjusza, przeciwko – co musiało bardzo boleć – Anglikowi z jego nie do przyjęcia, absurdalną wręcz matematyczną teorią oddziaływań na odległość.
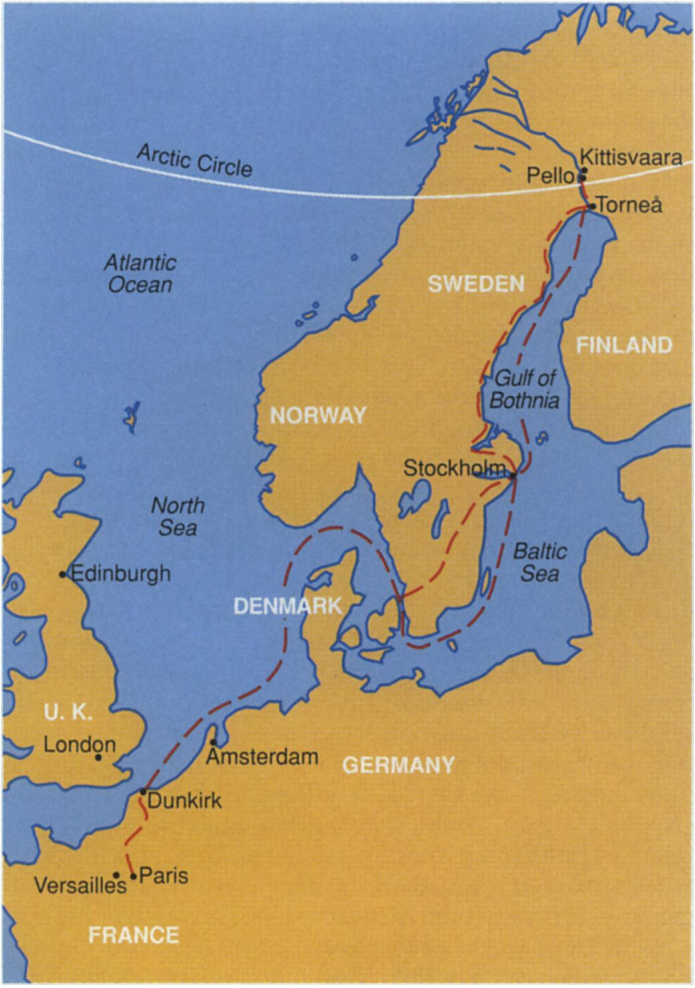
Rekonstrukcja trasy wyprawy Maupertuisa do Pello w Laponii
Dwie wyprawy.
Akademia Francuska postanowiła wysłać dwie wyprawy w celu rozstrzygnięcia problemu kształtu Ziemi: jedną na równik, do obecnego Ekwadoru, a drugą na koło podbiegunowe, do Laponii. Porównanie długości jednego stopnia południka w tych miejscach oraz w Paryżu rozwiązałoby problem. Uzyskawszy zgodę i wsparcie króla Ludwika XV, obie wyprawy wyruszyły prawie w tym samym czasie. Wyprawa na równik wyruszyła w 1735 roku i przywiozła wyniki (w istocie chodziło o jedną liczbę!) dopiero po wielu latach, natomiast nieco późniejsza wyprawa do Laponii wróciła z odpowiedzią już po niespełna półtora roku. Z punktu widzenia samego problemu określenia kształtu Ziemi wyprawa na równik pełniła rolę awaryjnej, okazało się to jednak dopiero po powrocie ekspedycji z Laponii – mimo początkowych kontrowersji wyniki z Laponii porównane z wynikami z Paryża rozstrzygały problem.
W tym artykule przedstawimy krótko wyprawę do Laponii, odsyłając zaciekawionego Czytelnika do barwnych opisów obu wypraw w [Ferreiro, 2011], [Terrall, 2006] i [Hoare, 2017]. Przedtem jednak przypomnimy interesujące nas tu osiemnastowieczne teorie pomiarowe w geodezji.
Metoda Newtona i metody pomiarowe.
Metoda Newtona określenia kształtu planet opierała się na prostej argumentacji dotyczącej kształtu samograwitującego płynu. Zajrzyjmy do Principiów.
Księga III, Teza XVIII. Twierdzenie XVI. Osie planet są krótsze od średnic wytyczonych prostopadle do osi.
Gdyby poszczególne części planety nie były poddane dobowemu ruchowi krążącemu, to jednakowe siły ciążenia, działające na części planety znajdujące się po każdej z jej stron, uformowałyby jej sferyczny kształt. Ten krążący ruch sprawia, że części planety odległe od osi starają się unieść ponad równik i dlatego, gdy materia jest w stanie płynnym, to unosząc się ponad równik, powiększy średnicę planety w tym miejscu, a opadając w okolicy biegunów – skróci jej oś. Stąd według zgodnych obserwacji astronomów średnica Jowisza jest krótsza między biegunami niż mierzona ze wschodu na zachód (…).
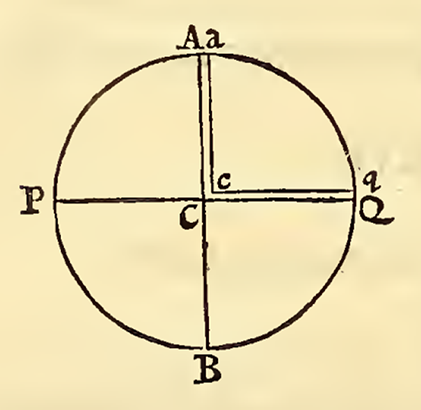
Eksperyment hydrodynamiczny Newtona. Księga III, Teza XX. Zadanie IV. Znaleźć i porównać ze sobą ciężary ciał w różnych miejscach na Ziemi.
,,Skoro ciężary wody w różnych odnogach wypełnionego wodą kanału ACQqca są jednakowe, zaś ciężary części tej wody proporcjonalnych do całej zawartości odnóg, i podobnie w nich położonych, są do siebie w proporcji ciężarów zawartości całych odnóg i dlatego są jednakowe, to ciężary jednakowych i podobnie położonych w poszczególnych odnogach części będą odwrotnie proporcjonalne do tych odnóg, czyli w stosunku odwrotnym niż 230 do 229”.
Ponieważ w czasach Newtona nie były jeszcze znane metody matematyczne potrzebne do uzyskania obliczeń dla powyższego problemu, przeprowadził on eksperyment myślowy z kanałami wypełnionymi płynem (zob. rysunek na marginesie). Na jego podstawie po długich obliczeniach Newton wywnioskował, że średnica Ziemi na równiku \(D_E\) ma się do średnicy między biegunami \(D_P\) tak, jak 230 do 229, a zatem spłaszczenie na biegunie wynosi \((D_E-D_P)/D_E,\) czyli \(1/230,\) co jest bardzo bliskie współczesnym obliczeniom dającym \(1/298.\)
Jak wspomnieliśmy, obliczenia Newtona były uzgodnione z wynikiem eksperymentu Jeana Richera z zegarem wahadłowym. Aby zegar w Cayenne (skalibrowany tak, by okres wahadła odpowiadał jednej sekundzie) wskazywał dokładny czas, Richer musiał nieco skrócić wahadło (o \(2{,}256\) mm). Ponieważ długość wahadła jest proporcjonalna do lokalnego przyspieszenia grawitacyjnego, zgodnie ze wzorem \(g = (2\pi/T)^2 l\) (\(g\) – przyspieszenie grawitacyjne, \(T\) – okres wahadła, \(l\) – długość wahadła), wynik Richera oznaczał, że grawitacja w Cayenne jest nieznacznie słabsza (o \(0{,}28\%\)) od grawitacji w Paryżu, co sugeruje, że rzeczywiście coś jest nie tak z kształtem Ziemi. Richer jako pierwszy zaobserwował zmianę siły grawitacji nad powierzchnią Ziemi, zapoczątkowując w ten sposób naukę o grawimetrii.
W XVIII wieku istniały dwa sposoby pomiaru odchyleń kształtu Ziemi od sfery: wspomniane wyżej porównanie zegarów wahadłowych na różnych szerokościach geograficznych oraz pomiar długości dostatecznie długiego odcinka południka. Ten drugi sposób opierał się na triangulacji, metodzie stosowanej przez geodetów i twórców map, pozwalającej (prawie) sprowadzić pomiar odległości do pomiaru kątów.
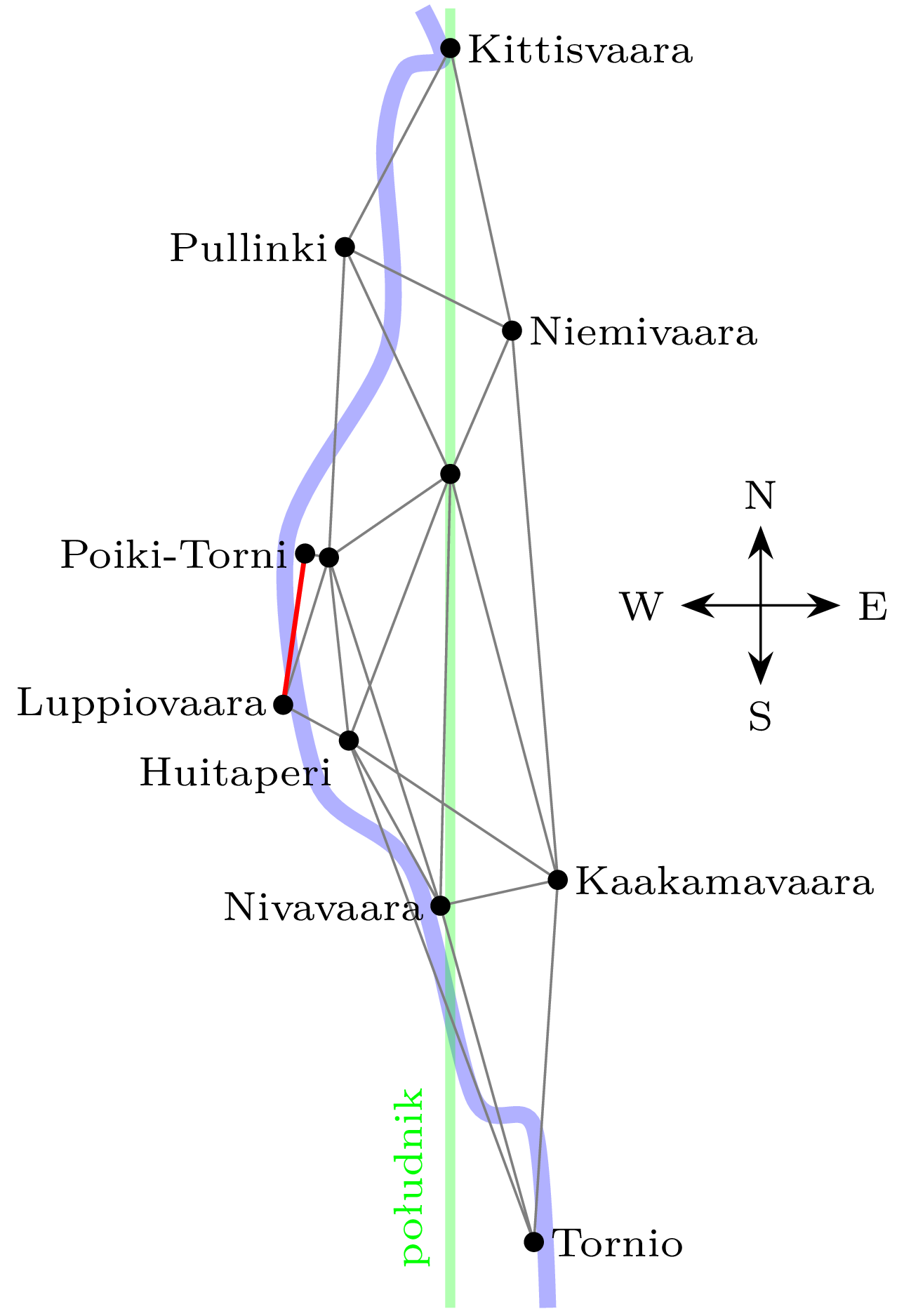
Dokonana przez wyprawę Maupertuisa triangulacja wzdłuż rzeki Tornio, od wieży kościoła w Tornio na południu po wzgórze Kittisvaara, oddalone o \(4\) km na północ od wioski Pello. Linię bazową (oznaczoną kolorem czerwonym) o długości \(14{,}3\) km zmierzono na pokrytej lodem rzece Tornio. Znajomość wszystkich kątów siatki wraz z długością linii bazowej wyznacza wszystkie pozostałe odległości.
By dokonać pomiaru odległości, zaczynamy od wyznaczenia siatki trójkątów pokrywających interesujący nas obszar – w naszym przypadku trójkąty muszą być ułożone mniej więcej wzdłuż południka (zob. rysunek obok). Następnie obserwatorzy przemieszczają się od jednego wierzchołka siatki do drugiego, by zebrać pomiary kątów we wszystkich trójkątach – dla ułatwienia obserwacji m.in. buduje się wieże triangulacyjne. Znajomość kątów wyznacza jednoznacznie kształt całej siatki, pozostaje więc dokonać pomiaru zaledwie jednego boku jednego z trójkątów, tak zwanej linii bazowej (na rysunku obok na czerwono). Ponieważ w danym trójkącie znajomość kątów oraz jednego boku pozwala wyznaczyć pozostałe boki, więc wszystkie długości w siatce można otrzymać przez serię obliczeń. Zaletą tej metody jest to, że kąty są znacznie łatwiejsze do precyzyjnego pomiaru niż odległości liniowe, zwłaszcza w zróżnicowanym terenie. [wg Terral, 2006].
Teoria pomiarów jest prosta, gorzej z praktyką. Są tu dwa problemy. Jeden dotyczy samego zbierania pomiarów w trudnym terenie, ich dokładności, która zależy od człowieka i użytych instrumentów, podobnie jak dokładności również trudnych pomiarów astronomicznych. Drugi problem dotyczy właściwego odczytania zebranych pomiarów, które zależy od dokonania właściwych poprawek wyników triangulacji (odwzorowanie siatki na płaszczyznę na poziomie morza) i poprawek pomiarów astronomicznych, z uwzględnieniem refrakcji atmosferycznej i aberracji świetlnej (paralaksa gwiezdna nie mogła być jeszcze w owym czasie dostrzeżona).
Maupertuis w Laponii.
Kadrę naukową piętnastoosobowej wyprawy Maupertuisa (lat 38) stanowiła zgrana grupa znakomitych uczonych. Należeli do niej on sam – jako lider wyprawy, jego bliscy koledzy, matematyk Alexis Clairaut (22 l.) i astronom Anders Celsjusz (35 l.), a także astronom Pierre-Charles Le Monnier (21 l.).
Alexis Clairaut (1713–1765) był cudownym dzieckiem, swój pierwszy artykuł przesłał do Akademii w 1726 roku, w wieku dwunastu lat, wykazując się już biegłością w rachunku różniczkowym i teorii krzywych algebraicznych. Do Akademii został przyjęty, za specjalną dyspensą króla, w niezwykle młodym wieku osiemnastu lat. Jeszcze przed wyprawą napisał cały szereg prac z zakresu teorii krzywych, maksimów i minimów, a także geometrii niesferycznej Ziemi i metod wyznaczania jej kształtu. Pomimo krótkowzroczności Clairauta jego udział w wyprawie był uzasadniony niezwykłymi umiejętnościami matematycznymi i rachunkowymi. W tej wyprawie wyrafinowana matematyka była równie ważna, jak precyzyjne obserwacje.
Pion zenitalny George’a Grahama, wykonany specjalnie na potrzeby wyprawy do Laponii. Teleskop o długości dziewięciu stóp zwisa z wierzchołka drewnianej ramy; obserwacji dokonuje się w pozycji półleżącej. (Maupertuis, Degré du méridien entre Paris et Amiens)
Anders Celsjusz (1701–1744) został profesorem astronomii na Uniwersytecie w Uppsali w wieku 29 lat. Po powrocie z wyprawy doprowadził do utworzenia w Szwecji pierwszego uniwersyteckiego obserwatorium. Opublikował oryginalny katalog jasności około 300 gwiazd i należał do pierwszych uczonych, którzy stwierdzili magnetyczny charakter zjawiska zórz polarnych. W historii fizyki zapisał się przez zaproponowanie znanej wszystkim skali temperatur, co prawda odwróconej w stosunku do tej używanej obecnie. Był jedynym uczestnikiem wyprawy mającym solidne doświadczenie astronomiczne. Do jego roli należał wybór najprecyzyjniejszych dostępnych instrumentów pomiarowych, zegarów wahadłowych, pionów zenitalnych etc. Zamówił je u najlepszego wytwórcy instrumentów pomiarowych w Europie, samego George’a Grahama z Londynu. Instrumenty były bardzo drogie, na przykład duży pion zenitalny kosztował aż 130 funtów – aby uzyskać przybliżony współczesny odpowiednik w dolarach amerykańskich, należy przemnożyć tę liczbę przez 360. Użycie najnowszych instrumentów wymagało też nabycia nowych umiejętności obserwacyjnych. Udział w wyprawie Celsjusza, Szweda, był też uzasadniony jego znajomością języka oraz proponowanych terenów pomiarowych, które leżały wówczas na terytorium Szwecji.
Pierre-Charles Le Monnier (1715–1799) został przyjęty do Akademii w wieku 20 lat na podstawie jego obserwacji astronomicznych, sporządzenia rozbudowanej mapy Księżyca i opracowań na temat Saturna i Księżyca. Jego wspaniała kariera obejmowała między innymi co najmniej 12 obserwacji planety Uran, których dokonywał w latach 1765–1769, jeszcze przed jej zidentyfikowaniem jako planety przez Williama Herschela w 1781 roku – obserwacje były później pomocne w wyznaczeniu orbity nowej planety.
Aby przybliżyć Czytelnikowi choć trochę trudy ekspedycji do Laponii, zacytujmy kilka fragmentów z książki Maupertuisa ,,Figure de la terre” z 1738 roku.
Musieliśmy przeprowadzić pomiary, które byłyby trudne na najbardziej przystosowanych do tego obszarach, na pustkowiach kraju prawie nienadającego się do zamieszkania, w tym ogromnym lesie, który rozciąga się od Torneå [Tornio] aż po Przylądek Północny. Istniały tylko dwa sposoby przedostania się w tę dzicz i trzeba było skorzystać z obu: jednego, przemierzając rzekę pełną katarakt, drugiego, przechodząc pieszo gęste lasy lub głębokie bagna. Zakładając, że uda nam się przedostać w głąb kraju, należałoby po możliwie najcięższej wędrówce wspiąć się na strome góry i oczyścić ich szczyty z drzew zasłaniających widok. Trzeba byłoby żyć na tej pustyni z najgorszym jedzeniem, narażonym na ataki tak złośliwych owadów, że zmuszają Lapończyków i ich renifery do opuszczenia tej części kraju latem.
Tabela obserwacji kątowych z La figure de la terre, jedna z wielu stron danych odpowiadających diagramom geometrycznym trójkątów. W tabeli przedstawiono pomiary zredukowane do płaszczyzny horyzontu i stosowne poprawki
Na rzece dotkliwie nękały nas duże, zielonogłowe muchy, które wykrwawiały nas wszędzie tam, gdzie nas użądliły. Znaleźliśmy się na [górze] Niwie prześladowani przez kilka innych, jeszcze bardziej okrutnych rodzajów.
Dym nie mógł nas obronić przed owadami, bardziej okrutnymi na tej górze niż na Niwie. Pomimo wielkiego upału musieliśmy owinąć głowy w szaty ze skór reniferów i schować się pod grubym wałem z gałęzi sosnowych i całych sosen, które nas przygniatały i nie zapewniły nam bezpieczeństwa na długo.
Nie powiem nic o trudach i niebezpieczeństwach tej operacji; możecie sobie wyobrazić, co to znaczy chodzić po dwóch stopach śniegu, niosąc ciężkie kije pomiarowe, które trzeba stale wbijać w śnieg i podnosić. Wszystko to przy tak silnym zimnie, że gdy próbowaliśmy napić się eau de vie [brandy], jedynego napoju, który można zachować w stanie płynnym, język i wargi natychmiast przymarzały do kubka i można je było oderwać jedynie z krwią.
Kontrowersje po wyprawie. Porównania wyników z Laponii i Francji.
Jeszcze przed wyprawą do Laponii Johann Bernoulli, zwolennik Cassinich, zapytał: Czy obserwatorzy mają jakieś upodobanie do jednej lub drugiej z tych idei? (…) Bo jeśli wierzą, że Ziemia jest spłaszczona na biegunach, z pewnością przekonają się, że jest ona spłaszczona… Dlatego będę wytrwale czekać na wyniki obserwacji amerykańskich.
Na wyniki z równika trzeba było czekać do połowy 1744 roku, natomiast ekspedycja Maupertuisa, która wyruszyła w kwietniu 1736 roku, już siedemnaście miesięcy później przywiozła do Paryża następujący wynik pomiarów: stopień szerokości geograficznej Laponii wynosi \(57\,437\) sążni, czyli o \(477\) sążni więcej niż łuk paryski zmierzony przez Cassinich w 1718 r. Pod koniec sierpnia Maupertuis oświadczył członkom Akademii, że jest oczywiste, że Ziemia jest znacznie spłaszczona na biegunach”.
Rozjątrzony Cassini odrzucił te wyniki jako niemiarodajne. Stwierdził, że Maupertuis zmierzył zbyt krótki fragment południka, by zagwarantować wiarygodny pomiar, że jego pomiary triangulacji terenu były niewiarygodne, gdyż były oparte na pomiarach tylko jednej linii bazowej, a nie dwóch, jak to powinno być zrobione, oraz że nie skalibrował właściwie pomiarów astronomicznych.
Kiedy dane Maupertuisa przeanalizowano i porównano z wcześniejszymi pomiarami we Francji, okazało się, że średnica Ziemi pomiędzy biegunami była mniejsza niż jej średnica równikowa o 1 część na 178. Spłaszczenie Ziemi na biegunach było zatem dużo większe niż wartość \(1/230,\) którą pierwotnie przewidywał Newton. W tej sytuacji wszyscy pragnęli poznać wyniki ekspedycji na równik. Po sześciu latach ogłoszono jej wyniki: długość jednego stopnia południka wyniosła tam około \(56\,750\) sążni, co tylko potwierdziło słuszność teorii Newtona.
Artykuł rozpoczęliśmy sarkastyczną uwagą Woltera o Cassinich i w podobnej tonacji go zakończymy. Wolter zakpił sobie tym razem z samego Maupertuisa, wypowiadając następującą uwagę:
W tych trudnych miejscach potwierdziłeś to, co wiedział pan Newton, nie wychodząc z domu.
Bibliografia
J. Donald Fernie, The Shape of the Earth, Part III, American Scientist , Vol. 80, No. 2 (March-April 1992), pp. 125-127.
Laurie D. Ferreiro, Measure of the Earth. An Enlightment Expedition that Reshaped our World, Basic Books, New York 2011.
H. Bentley Glass, Maupertuis and the Beginnings of Genetics, The Quarterly Review of Biology, Vol. 22, No. 3 (Sep., 1947), The University of Chicago Press, 196-210.
H. Bentley Glass, Maupertuis, a Forgotten Genius, Scientific American , Vol. 193, No. 4 (October 1955), pp. 100-111.
Michael R. Hoare, The Quest for the True Figure of the Earth, Routledge, New York 2017.
Miljenko Solarić, Nikola Solarić, French Geodetic and Scientific Expedition to Lapland, KiG No. 22, Vol. 13, 2014.
Mary Terrall, The Man who Flattened the Earth, The University of Chicago Press, 2006.