Zadania z matematyki nr 883, 884
Termin nadsyłania rozwiązań: 31 VIII 2024
Redaguje Marcin E. KUCZMA
883. Znaleźć wszystkie funkcje \({f\colon{\mathbb R}\to{\mathbb R}}\) spełniające równanie \[f(x^2+y^2)=f(x^2)+f(xy)+f(y^2)\ \ \ \ \hbox{dla}\;\;x,y\in{\mathbb R}.\]
884. Wykazać, że dla każdej pary liczb naturalnych \({a\ge2},\) \({b\ge1}\) istnieje nieskończenie wiele takich liczb naturalnych \(n,\) że liczba \({ba^n+1}\) jest złożona.Czołówka ligi zadaniowej Klub 44 M
po uwzględnieniu ocen rozwiązań zadań
869 (\(WT = 1{,}34\)) i 870 (\(WT = 2{,}50\))
z numeru 11/2023
Marek Spychała Warszawa 45,31 Jerzy Cisło Wrocław 45,14 Janusz Olszewski Warszawa 44,73 Paweł Najman Kraków 44,50 Janusz Fiett Warszawa 43,82 Paweł Kubit Kraków 41,99 Adam Woryna Ruda Śl. 40,91 Piotr Wiśniewski Warszawa 40,81 Piotr Kumor Olsztyn 40,44 Łukasz Merta Kraków 37,42 Szymon Kitowski 34,48 Witold Bednarek Łódź 32,56 Wszyscy czterej Panowie są z nami od lat i zaliczają, jedno po drugim, kolejne okrążenia bieżni 44p.: pan Marek Spychała po raz piąty; pan Jerzy Cisło po raz siedemnasty; pan Janusz Olszewski po raz dwudziesty czwarty; pan Paweł Najman po raz dziewiąty (jakże niepozornie jawi się przy tych wynikach honor Weterana, przyznawany już po trzecim okrążeniu…).
Zadanie 884 zaproponował pan Witold Bednarek z Łodzi
Rozwiązania zadań z numeru 2/2024
Przypominamy treść zadań:
875. Dany jest ciąg \((x_1,\ldots,x_N)\) o wyrazach \({x_i\in\{0,1\}}\) (\(N\) jest ustaloną liczbą nieparzystą). Niech \({a_k=\sum_{i<k}x_i},\) \({b_k=\sum_{i>k}(1-x_i)},\) \({c_k=a_k+b_k}\) (dla \({k=1,\ldots,N})\). Wiadomo, że dokładnie jedna liczba \(z\) występuje w ciągu \((c_1,\ldots,c_N)\) nieparzyście wiele razy. Dla ustalonego \(N\) wyznaczyć wszystkie możliwe wartości \(z.\)
Znajdujemy w ciągu \((x_i)\) blok 10 (jeśli istnieje) i wykonujemy transpozycję \({10\mapsto01}.\) To znaczy, znajdujemy dowolny numer \({\ell<N},\) dla którego \({x_\ell=1},\) \({x_{\ell+1}=0}\) (więc \({a_{\ell+1}=a_\ell+1},\) \({b_{\ell+1}=b_\ell-1},\) \({c_{\ell+1}=c_\ell}\)) i tworzymy ciąg \((x'_1,\ldots,x'_N),\) przyjmując \[x'_\ell=0,\ \ \ x'_{\ell+1}=1,\ \ \ x'_i=x_i\ \ \ \hbox{dla}\;i\ne\ell,\ell{+}1.\] Określamy (jak dla ciągu \((x_i)\)): \({a'_k=\sum_{i<k}x'_i},\) \({b'_k=\sum_{i>k}(1-x'_i)},\) \({c'_k=a'_k+b'_k}.\) Wtedy \[\displaylines{ a'_k=a_k,\ \ \ b'_k=b_k\ \ \ \hbox{dla}\;k\ne\ell,\ell{+}1;\cr a'_\ell=a_\ell,\ \ \ a'_{\ell+1}=a_\ell-1,\ \ \ b'_\ell=b_\ell-1,\ \ \ b'_{\ell+1}=b_{\ell+1}.\cr }\]
Stąd \[c'_\ell=c_\ell-1,\ \ \ c'_{\ell+1}=c_{\ell+1}-1,\ \ \ c'_k=c_k\ \ \ \hbox{dla}\;k\ne\ell,\ell{+}1.\] Każda wartość, wcześniej obecna [lub nieobecna] w ciągu \((c_i),\) mogła zniknąć [lub pojawić się] jedynie jednocześnie na dwóch pozycjach. Wobec tego wartość \(z\) powinna wystąpić w ciągu \((c'_k)\) nadal nieparzyście wiele razy, a każda inna wartość – parzyście wiele razy.
Powtarzając takie transpozycje, doprowadzamy ciąg \((x_i)\) do postaci bez sekwencji 10; czyli do postaci \((\underbrace{0,\ldots,0}_s,\underbrace{1,\ldots,1}_{N-s})\); liczba wystąpień dowolnej wartości nie zmieniła przy tym parzystości. Uzyskany ciąg generuje (jak w treści zadania) ciągi \((a_k),\) \((b_k)\) dane jawnymi wzorami: \[a_k=\begin{cases} 0&\text{dla $k\le{s},$}\\ k{-}s{-}1&\text{dla $k>s,$}\\ \end{cases} \ \ \ \ b_k=\begin{cases} s{-}k&\text{dla $k\le{s},$}\\ 0&\text{dla $k>s.$}\\ \end{cases}\] Ciąg \((c_k)\) wygląda teraz tak: \[(\underbrace{s{-}1,s{-}2,\ldots,1,0}_s,\underbrace{0,1,\ldots,N{-}s{-}2,N{-}s{-}1}_{N-s}).\] Wyrazy centralne grupują się w pary. Liczba \(z,\) która ma wystąpić nieparzyście wiele razy – co teraz oznacza: dokładnie jeden raz – i być przy tym jedyną o tej własności, musi być jednym ze skrajnych wyrazów; zaś grupowanie w pary musi objąć wszystkie wyrazy pozostałe. To znaczy: wyraz pierwszy musi być równy przedostatniemu (\({s{-}1=N{-}s{-}2},\) i wtedy \({z=N{-}s{-}1}\)); lub wyraz drugi równy ostatniemu (\({s{-}2=N{-}s{-}1},\) i wtedy \({z=s{-}1}\)). W pierwszym przypadku \({s={1\over 2}(N-1)}\); w drugim \({s={1\over 2}(N+1)}.\) W obu przypadkach \({z={1\over 2}(N-1)}.\) Jest to jedyna możliwa wartość, o jaką pyta zadanie. Uzyskiwana jest dla każdego ciągu \((x_i),\) w którym liczba zer (czyli \(s\)) różni się o 1 od liczby jedynek.
Regulamin Ligi znajduje się na naszej stronie:
www.deltami.edu.pl/klub-44/ regulamin/
876. Wykazać, że dla liczb \({x,y,z\ge0}\) o sumie 3 zachodzi nierówność \[{x\over y^2+y+1}+{y\over z^2+z+1}+{z\over x^2+x+1}\ge1.\]
Funkcja \({f(t)=(t^2+t+1)^{-1}}\) ma pochodną drugiego rzędu, wyrażającą się wzorem \({f''(t)=6(t^2+t+1)^{-3}(t^2+t)},\) dodatnią dla \({t\ge0},\) co oznacza, że \(f\) jest wypukła w przedziale \([0,\infty).\) Stosujemy nierówność Jensena (z wagami \({x\over 3},{y\over 3},{z\over 3},\) o sumie 1): \[{x\over 3}\,f(y)+{y\over 3}\,f(z)+{z\over 3}\,f(x)\ge f\Bigl({xy\over 3}+{yz\over 3}+{zx\over 3}\Bigr).\] Wyrażenie po lewej stronie – to suma dana w zadaniu, podzielona przez 3. Wystarczy zatem dowieść, że dla \({w=xy+yz+zx}\) zachodzi nierówność \({f(w/3)\ge1/3}.\)
Ponieważ \({w\le{x^2+y^2+z^2}},\) więc \({3w\le2w+(x^2+y^2+z^2)=(x+y+z)^2=9},\) czyli \({w/3\le1}.\) Funkcja \(f\) jest malejąca w przedziale \([0,\infty),\) zaś \({f(1)=1/3}.\) Stąd \({f(w/3)\ge1/3}.\)
Zadania z fizyki nr 780, 781
Termin nadsyłania rozwiązań: 31 VIII 2024
Redaguje Elżbieta ZAWISTOWSKA
780. Mała piłeczka spadająca z wysokości \(h\) na twardą podłogę odskakuje na wysokość \(h/3.\) Na niciach o długościach \(l\) zawieszono stykające się ze sobą dwie takie piłeczki. Jedną z nich odchylono od pionu o kąt \(\pi/2\) i puszczono swobodnie. O jakie kąty odchylą się nici po zderzeniu piłeczek?
Czołówka ligi zadaniowej Klub 44 F
po uwzględnieniu ocen rozwiązań zadań
766 (\(WT=3{,}06\)), 767 (\(WT=1{,}86\)) z numeru 11/2023
Marian Łupieżowiec Gliwice 3 – 44 + 0,88 Jacek Konieczny Poznań 38,28 Ryszard Baniewicz Włocławek 1 – 35,93 Konrad Kapcia Poznań 2 – 35,60 Paweł Perkowski Ożarów Maz. 5 – 31,19 Andrzej Nowogrodzki Chocianów 3 – 22,39 Jan Zambrzycki Białystok 4 – 17,82
Rys. 1
781. W odległości \(R\) od nieruchomego ładunku \(Q>0\) znajduje się mała kulka o masie \(m,\) naładowana ładunkiem \(-Q.\) Układ znajduje się w jednorodnym polu magnetycznym, którego linie pola są prostopadłe do odcinka łączącego ładunki. Po oswobodzeniu kulka zaczyna się poruszać, a minimalna odległość, na jaką zbliża się do nieruchomego ładunku, wynosi \(R/2.\) Znaleźć wartość indukcji pola magnetycznego.
Rozwiązania zadań z numeru 2/2024
Przypominamy treść zadań:
772. Rakieta jest rozpędzana w wyniku wyrzucania ciągłego strumienia gazu, którego prędkość względem rakiety jest stała i wynosi \(v_0.\) Początkowa prędkość rakiety jest równa zeru. Ile wynosi prędkość rakiety, gdy jej energia kinetyczna osiąga wartość maksymalną? Siłę ciężkości zaniedbujemy.
Gdy energia rakiety osiąga wartość maksymalną, jej pochodna po czasie jest równa zeru: \[{d\over dt}\left({1\over 2}Mv^2\right)={1\over 2}{dM\over dt}v^2+{1\over 2}M2v{dv\over dt}=0,\] gdzie przez \(M\) oznaczyliśmy masę rakiety, stąd jej prędkość \[v={2M\over\mu }{dv\over dt}.\] \(\mu =-{dM}/{dt}\) jest stałą masą gazu wypływającego z rakiety w jednostce czasu.
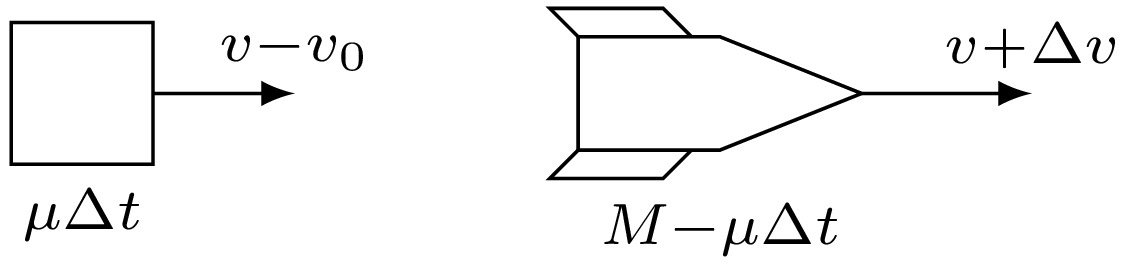
Przyspieszenie rakiety \(a\) znajdziemy z zasady zachowania pędu układu rakieta–gaz, dla bardzo małego przedziału czasu (rys. 2): \[Mv=\mu \Delta t\left(v-v_0\right)+\left(M-\mu \Delta t\right)\left(v+\Delta v\right).\] Uwzględniając, że \(\mu \Delta t\ll M,\) otrzymujemy \[a={\Delta v}/{\Delta t={\mu v_0}/{M}}.\] Szukana prędkość, odpowiadająca maksymalnej energii kinetycznej rakiety, jest równa \(2v_0.\)
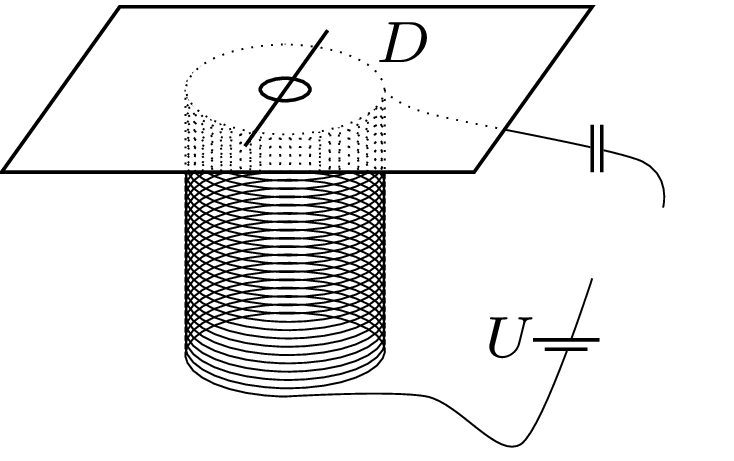
773. Na górze ustawionej pionowo zwojnicy leży cienki kawałek kartonu, a na nim mały nadprzewodzący pierścień z cienkiego drutu, którego średnica \(d_1\) jest znacząco mniejsza od średnicy pierścienia \(D\ \)(rys. 1). Po podłączeniu zwojnicy do źródła napięcia \(U\) szeregowo z kondensatorem pierścień podskakuje, gdy \(U>U_0.\) Jakie powinno być napięcie źródła w analogicznym doświadczeniu z pierścieniem o takiej samej średnicy, ale wykonanego z drutu o średnicy \(d_2\)? Współczynnik samoindukcji takiego pierścienia wynosi w przybliżeniu \(L= kDln\left(1{,}4D/d\right).\) Opór zwojnicy możemy pominąć.
Prawo Kirchhoffa dla zamkniętego obwodu zwojnicy o zaniedbywalnym oporze ma postać: \[U-L_z{dI_z\over dt}={Q\over C},\] gdzie \(L_z\) jest indukcyjnością zwojnicy, \(Q\) ładunkiem na kondensatorze o pojemności \(C,\) a \(I_{z\ }\)natężeniem prądu w obwodzie. Korzystając ze związku \(I_z={dQ}/{dt},\) mamy: \[{d^2Q\over dt^2}+{Q\over L_zC}={U\over L_z}.\] Wprowadzając oznaczenia \({1}/{L_zC}={\omega }^2\) i \(q=Q-UC,\) otrzymujemy równanie oscylatora harmonicznego: \[{d^2q\over dt^2}+{\omega }^2q=0,\] z warunkami początkowymi w chwili zamknięcia klucza: \[q\left(0\right)=Q\left(0\right)-UC=-UC\ \ \ \text{oraz}\ \ \ {dq\over dt}% (0)=I_z\left(0\right)=0.\] Rozwiązanie tego równania ma postać: \[q\left(t\right)=-UC\cos\omega t,\] stąd \(I_z(t)=UC\omega \sin\omega t.\) Natężenie prądu \(I\) w nadprzewodzącym pierścieniu o indukcyjności \(L\) znajdziemy z równania \[-{d\phi \over dt}-L{dI\over dt}=0,\] gdzie \(\phi\) jest zewnętrznym strumieniem pola magnetycznego przez powierzchnię pierścienia. W chwili początkowej \(\phi \left(0\right)=0,\) zatem \(I=-{\phi }/{L}.\) Strumień \(\phi\) jest proporcjonalny do powierzchni pierścienia oraz do wartości wektora indukcji w zwojnicy, który z kolei jest proporcjonalny do natężenia prądu w zwojnicy: \(\phi \sim I_zD^2\sim UD^2.\) Uwzględniając to, otrzymujemy \[I\sim {UD^2\over L}.\] Maksymalna wartość siły elektrodynamicznej \(F\) działającej na pierścień w kierunku pionowym jest proporcjonalna do długości pierścienia, natężenia prądu w zwojnicy i natężenia prądu w pierścieniu: \[F\sim DII_z\sim {D^3U^2\over L}.\] Pierścień będzie podskakiwać, gdy siła \(F\) będzie większa od siły ciężkości działającej na pierścień, proporcjonalnej do \(Dd^2.\) W granicznym przypadku, gdy siły te równoważą się, \(D^3U^2/L\sim Dd^2,\) stąd \(U\sim d\sqrt{L}/D.\) W pierwszym przypadku rozważanym w zadaniu \(U_0\sim {d_1\sqrt{L_1}}/{D},\) w drugim \({U_0}'\sim d_2\sqrt{L_2}/D.\) Napięcie źródła w drugim przypadku musi spełniać warunek: \[U>U_0'=U_0\sqrt{{ln\left(1{,}4D/d_2\right)\over ln\left(1{,}4D/d_1\right)}}{d_2\over d_1}.\]