Afiliacja: Wydział Matematyki i Fizyki Stosowanej, Politechnika Rzeszowska
Poszukiwanie odpowiedzi na trudne pytania może prowadzić do narodzin nowej teorii. Oto dwa odkrycia, które miały wpływ na powstanie teorii szeregów.
Nicole Oresme około 1350 roku zauważył, że skoro \(\frac{1}{k+1}+\frac{1}{k+2}+\ldots +\frac{1}{k+k}\geqslant k\cdot \frac{1}{2k}=\frac{1}{2}\) dla \(k=1,2,\ldots,\) to \[\begin{aligned} 1+\frac{1}{2}+\bigg(\underbrace{\frac{1}{3}+\frac{1}{4}}_{\geq \frac{1}{2} }\bigg)+\bigg(\underbrace{\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}}_{\geq\frac{1}{2}}\bigg)+\ldots +\bigg(\underbrace{\frac{1}{2^{k-1}+1}+\ldots +\frac{1}{2^k}}_{\geq\frac{1}{2}}\bigg)\geqslant \\ \geqslant 1+\frac{k}{2}\longrightarrow \infty,~~\hbox{gdy}~~k\rightarrow\infty. \end{aligned}\] Wykazał więc, że suma \(1+\frac{1}{2}+\frac{1}{3}+\ldots\) jest nieskończona. Trudno to przewidzieć, obliczając sumy początkowych wyrazów, bo \(1+\frac{1}{2}+\ldots +\frac{1}{k}>10\) dopiero dla \(k\geqslant 12376.\)
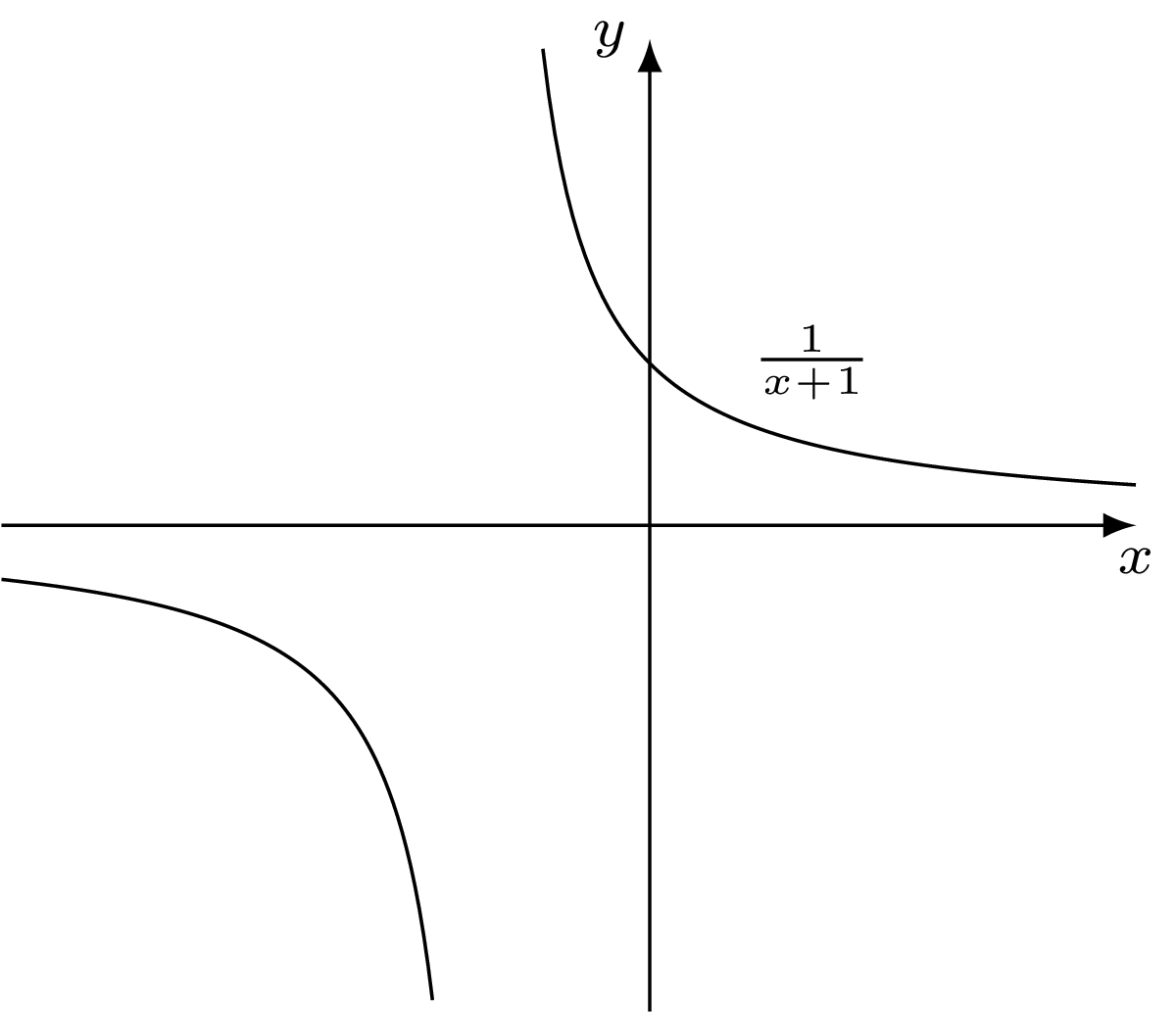
A co można powiedzieć o sumie \(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots\)? Problem wyznaczenia jej wartości okazał się trudny. Na odpowiedź przyszło nam czekać do drugiej połowy XVII wieku. Można jej upatrywać w pracach Johannesa Hudda (1656), Izaaka Newtona (1665), Nikolausa Mercatora, Johna Wallisa i Jamesa Gregory’ego (1668) nad kwadraturą hiperboli, tj. obliczaniem pola między osią \(OX\) a wykresem funkcji \(y(x)=\frac{1}{1+x},\) gdy \(0\leqslant x\leqslant a\) (gdy zastosujemy współczesne oznaczenia i nazewnictwo).
Przedstawimy teraz elementarny dowód tego, że \[\label{eq:log2} 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots =\ln 2.\tag{$\spadesuit$}\] Niech \(x_n=(1+\frac{1}{n})^n,\) \(y_n=(1+\frac{1}{n-1})^n\) dla \(n\geqslant 2.\) Oczywiście \[\tag{1}\label{eq:ineq} x_n\leqslant y_n~~\hbox{dla}~~n\geqslant 2.\] Ponadto \[\tag{2}\label{eq:mono} \textrm{ciąg $\{x_n\}$ jest niemalejący, a ciąg $\{y_n\}$ jest nierosnący, }\] co wykażemy za pomocą nierówności Jacoba Bernoulliego (1689): \((1+x)^n\geqslant 1+nx\) dla \(x>-1\) i naturalnego \(n\) (znanej już Newtonowi czy René-François de Sluse). Mamy bowiem \[\begin{aligned} \frac{x_{n+1}}{x_n}&=\frac{(1+\frac{1}{n+1})^{n+1}}{(1+\frac{1}{n})^n}=\bigg(1+\frac{1}{n}\bigg)\bigg(\frac{1+\frac{1}{n+1}}{1+\frac{1}{n}}\bigg)^{n+1}=\\ &=\bigg(1+\frac{1}{n}\bigg)\bigg(1-\frac{1}{(n+1)^2}\bigg)^{n+1}\geqslant \bigg(1+\frac{1}{n}\bigg)\bigg(1-\frac{1}{n+1}\bigg)=1,\\ \frac{y_n}{y_{n+1}}&=\frac{(1+\frac{1}{n-1})^n}{(1+\frac{1}{n})^{n+1}}=\frac{1}{(1+\frac{1}{n-1})}\bigg(\frac{1+\frac{1}{n-1}}{1+\frac{1}{n}}\bigg)^{n+1}=\\ &=\frac{1}{(1+\frac{1}{n-1})}\bigg(1+\frac{1}{(n-1)(n+1)}\bigg)^{n+1}\geqslant \frac{1}{(1+\frac{1}{n-1})}\bigg(1+\frac{1}{n-1}\bigg)=1. \end{aligned}\] Stwierdzenia \(\eqref{eq:ineq}\) i \(\eqref{eq:mono}\) gwarantują istnienie granic ciągów \(\{x_n\}\) i \(\{y_n\}.\) Ponieważ \(\frac{y_n}{x_{n-1}}=\frac{n}{n-1}\to 1,\) więc granice te są równe – ich wspólną wartość oznaczymy jako \(e\) (jest to słynna liczba Eulera). Ponownie powołując się na \(\eqref{eq:ineq}\) i \(\eqref{eq:mono}\), wnioskujemy, że \(x_n\leq e\leq y_n,\) czyli \[\tag{3}\label{eq:eineq} \bigg(1+\frac{1}{n}\bigg)^n\leqslant e\leqslant \bigg(1+\frac{1}{n-1}\bigg)^n,~~n\geqslant 2.{}\] Zauważmy teraz, że \[\begin{aligned} S_{2N}&=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots -\frac{1}{2N}=\\ &=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots +\frac{1}{2N}-2\bigg(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\ldots +\frac{1}{2N}\bigg)=\\ &=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots +\frac{1}{2N}-\bigg(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots +\frac{1}{N}\bigg)=\\ &=\frac{1}{N+1}+\frac{1}{N+2}+\ldots +\frac{1}{2N}. \end{aligned}\] Z własności funkcji wykładniczej mamy \(e^{S_{2N}}=\prod\limits_{n=N+1}^{2N}e^{\frac{1}{n}},\) zatem z nierówności \(\eqref{eq:eineq}\) otrzymujemy oszacowanie \[\prod\limits_{n=N+1}^{2N}\bigg(1+\frac{1}{n}\bigg)^\frac{n}{n}\leqslant \prod\limits_{n=N+1}^{2N}e^{\frac{1}{n}}\leqslant \prod\limits_{n=N+1}^{2N}\bigg(1+\frac{1}{n-1}\bigg)^\frac{n}{n},\] gdzie \[\begin{aligned} &\prod\limits_{n=N+1}^{2N}\bigg(1+\frac{1}{n}\bigg)=\frac{N+2}{N+1}\cdot \frac{N+3}{N+2}\cdot\ldots\cdot \frac{2N+1}{2N}=2-\frac{1}{N+1},\\ &\prod\limits_{n=N+1}^{2N}\bigg(1+\frac{1}{n-1}\bigg)=\frac{N+1}{N}\cdot \frac{N+2}{N+1}\cdot\ldots\cdot \frac{2N}{2N-1}=2. \end{aligned}\]
Kto zna całkę Riemanna, szybko dojdzie do celu: \[\begin{gathered} \lim\limits_{N\rightarrow\infty}\bigg(\frac{1}{N+1}+\frac{1}{N+2}+\ldots+\frac{1}{2N}\bigg)=\\=\lim\limits_{N\rightarrow\infty}\frac{1}{N}\sum\limits_{k=1}^{N}\frac{1}{1+\frac{k}{N}}=\int_{0}^{1}\frac{dx}{1+x}=\ln 2. \end{gathered}\]
Zatem \[2-\frac{1}{N+1}\leqslant e^{S_{2N}}\leqslant 2.\] Powyższa nierówność dowodzi, że \(\lim\limits_{N\rightarrow\infty} e^{S_{2N}}= 2.\) Określenie logarytmu naturalnego i ciągłość funkcji wykładniczej (\(e^x\)) zapewniają, że \(\lim\limits_{N\rightarrow\infty}S_{2N}=\ln 2.\) Ponieważ, \(S_{2N+1}=S_{2N}+\frac{1}{2N+1}\rightarrow \ln 2,\) gdy \(N\rightarrow\infty,\) więc
\[1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots = \ln 2,\] co kończy dowód.
Do wyznaczenia przybliżonej wartości \(\ln 2\) warto użyć szybciej zbieżnego rozwinięcia. James Gregory (1668) do obliczania logarytmów stosował równość \[\ln \frac{1+x}{1-x}=2\bigg(x+\frac{x^3}{3}+\frac{x^5}{5}+\ldots\bigg).\] Zatem \[\begin{aligned} \ln 2&=\ln \frac{1+\frac{1}{3}}{1-\frac{1}{3}}=2\bigg(\frac{1}{3}+\frac{1}{3\cdot 3^3}+\frac{1}{5\cdot 3^5}+\ldots\bigg)\approx 0{,}693. \end{aligned}\] Suma pierwszych trzech składników daje przybliżenie \(\ln 2\) z błędem względnym równym około \(0{,}2\%.\) Aby osiągnąć taką dokładność, potrzebowalibyśmy zsumować ponad 3000 pierwszych składników sumy \(\eqref{eq:log2}\).
Rachunek całkowy, sformułowany w czasach, o których piszemy, pozwalał otrzymywać ogólniejsze rezultaty. Dla \(x\neq-1,\) \[\frac{1}{1+x}=1-x+x^2-\ldots +(-1)^{n-1}x^{n-1}+\frac{(-1)^nx^n}{1+x}.\] Całkując to wyrażenie wyraz po wyrazie, mamy \[\begin{gathered} \ln (1+x)=\int_0^x\frac{dt}{1+t}=\\[-4pt]=\mbox{$\displaystyle x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots +(-1)^{n-1}\cdot \frac{x^n}{n}+(-1)^n\int_0^x\frac{t^n}{1+t}dt.$}\ \ \ \end{gathered}\] Jeśli \(0\leqslant x\leqslant 1,\) to \[\int_0^x\frac{t^n}{1+t}dt \leqslant \int_0^xt^ndt=\frac{x^{n+1}}{n+1}\leqslant \frac{1}{n+1}\longrightarrow 0,\] gdy \(n\rightarrow\infty,\) a wtedy \(\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots\) Przyjmując \(x=1,\) otrzymujemy \(\eqref{eq:log2}\). Z notatek znalezionych po śmierci Newtona wynika, że około 1665 roku znał on już rozwinięcie \[\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots\] i w elegancki sposób obliczył wartości \(\ln 2,\) \(\ln 3,\) \(\ln 5,\) \(\ln 7\) do 57 miejsca po przecinku. Uzyskane wyniki zachował jednak w tajemnicy.
Przyjmując \(x=-\frac{1}{2}\) w rozwinięciu \(\ln (1+x),\) otrzymamy ponadto wzór \[\ln 2 =\sum\limits_{n=1}^{\infty}\frac{1}{n2^n}\]
Podane rozwinięcie daje dobre rezultaty dla małych wartości \(x,\) dodatnich lub ujemnych, więc Newton obliczył przybliżone wartości dla \[\begin{aligned} &\ln (1{,}2)=\ln (1+0{,}2), ~\ln(0{,}98)=\ln(1-0{,}02),\\ &\ln (0{,}9)=\ln (1-0{,}1), ~\ln (0{,}8)=\ln (1-0{,}2), \end{aligned}\] a następnie wykorzystał równości \[\begin{aligned} \ln 2&= \ln\bigg(\frac{1{,}2\cdot 1{,}2}{0{,}8\cdot 0{,}9}\bigg)=2\ln(1{,}2)-\big(\ln(0{,}8)+\ln(0{,}9)\big),\\ \ln 3&= \ln\bigg(\frac{2\cdot 1{,}2}{0{,}8}\bigg)=\bigl(\ln 2+\ln(1{,}2)\big)-\ln(0{,}8),\\ \ln 5&= \ln\bigg(\frac{2\cdot 2}{0{,}8}\bigg)=2\ln 2-\ln(0{,}8),\\ \ln 7&=\mbox{$\displaystyle \ln \sqrt{\frac{100\cdot 0{,}98}{2}}=% \frac{1}{2}\big(10(\ln 2 +\ln 5)+\ln (0{,}98)-\ln 2\big).$} \end{aligned}\] Chapeau bas!