Czworokąt wypukły, w którym \(AB=AD,\) jest wpisany w okrąg. Punkty \(M\) i \(N\) leżą na odcinkach \(CD\) i \(BC\) tak, że \(DM+BN=MN.\) Udowodnić, że środek okręgu opisanego na trójkącie \(AMN\) leży na odcinku \(AC.\)
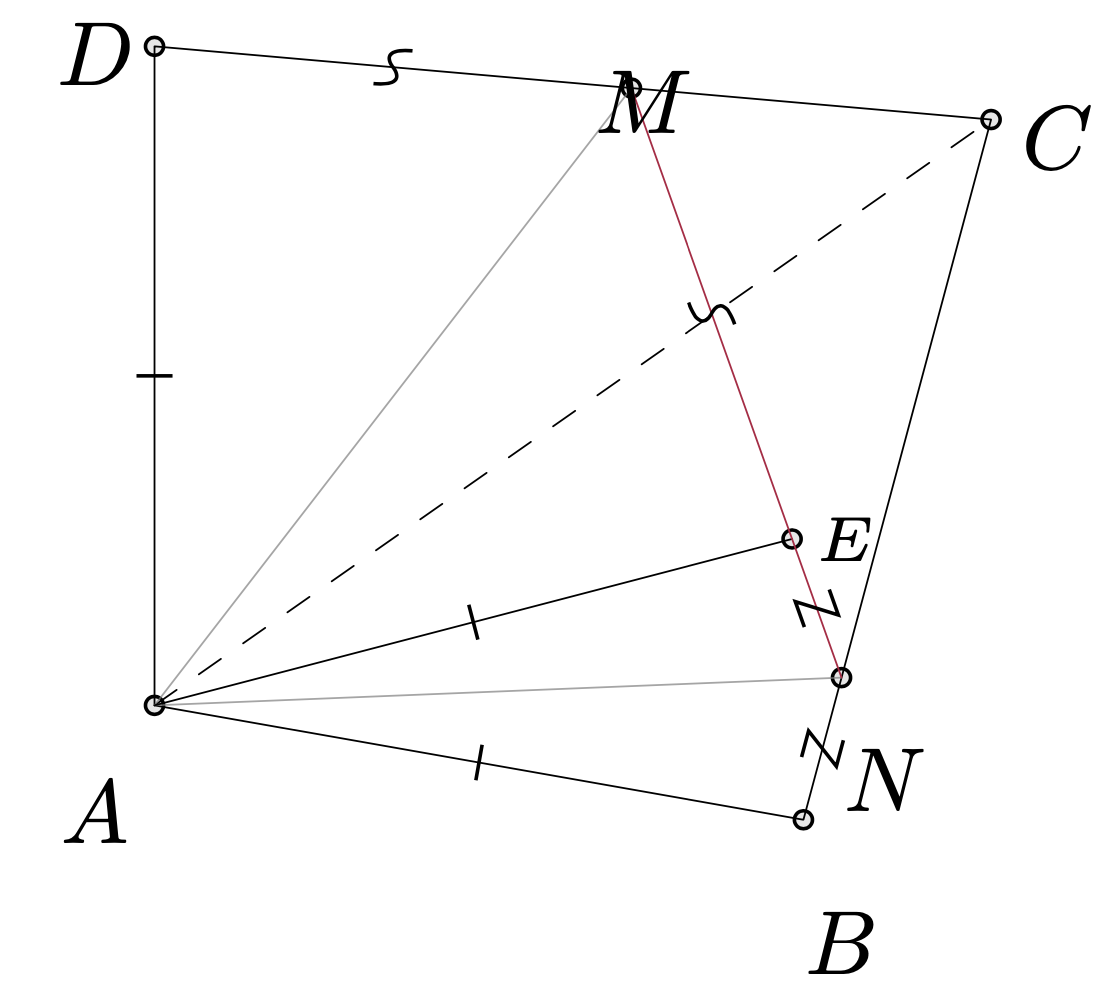
Zaznaczmy na odcinku \(MN\) taki punkt \(E,\) że \(EM = MD.\) Wtedy \(BN = NE.\) Wykorzystując równoramienność trójkątów \(EDM\) i \(EBN\) oraz równość \(\measuredangle ABC+\measuredangle CDA=180^\circ=\measuredangle MEN,\) dostajemy \[\measuredangle ABE+\measuredangle ADE = \measuredangle AEB + \measuredangle AED.\] Gdyby \(\measuredangle ABE > \measuredangle AEB,\) to \(\measuredangle ADE < \measuredangle AED,\) skąd \(AB < AE < AD,\) sprzeczność. Podobnie nie może zachodzić nierówność \(\measuredangle ABE < \measuredangle AEB.\) Zatem \(AB = AE = AD,\) więc pary trójkątów \(ABN\) i \(AEN\) oraz \(AEM\) i \(ADM\) są przystające. Wobec tego \[\begin{split} \measuredangle ANM +\measuredangle CAM&= \measuredangle ANB+\measuredangle CAM=\\ &=180^{\circ}-\measuredangle BAN-\measuredangle ABN+\measuredangle CAM=\\ &=180^{\circ}-\measuredangle BAN-\measuredangle ABD-\measuredangle MAD=\\ &=180^{\circ}-\frac{1}{2}\measuredangle BAD-\measuredangle ABD=90^\circ,\\ \end{split}\] co łatwo daje tezę zadania.
Znaleźć wszystkie liczby rzeczywiste dodatnie \(x\) i \(y\) takie, że \[2^{x^2+y}+2^{x+y^2}=128\ \ \ \textup{oraz}\ \ \ \sqrt{x}+\sqrt{y}=2\sqrt{2}.\]
Dane są liczby rzeczywiste \(a>b\) takie, że \(a^p-b^p\) jest liczbą całkowitą dla dowolnej liczby pierwszej \(p.\) Udowodnić, że \(a\) i \(b\) są liczbami wymiernymi.
Ponieważ \[\begin{gathered} (a^5-b^5)(a^{11}-b^{11})-(a^{13}-b^{13})(a^3-b^3)=\\=a^3b^3(a^2-b^2)^2(a^2+b^2)(a^4+b^4), \end{gathered}\] więc \[\begin{gathered} (a^3-b^3)^2+2a^3b^3+a^2b^2(a^2+b^2)=\\= (a^2+b^2)(a^4+b^4) \in \mathbb{Q}, \end{gathered}\] więc \(a^2+b^2\in \mathbb{Q}.\) Finalnie \[a-b=\frac{a^3-b^3}{a^2+ab+b^2}\ \ \textup{oraz}\ \ a+b=\frac{a^2-b^2}{a-b}\] są wymierne, skąd \(a\) i \(b\) też są wymierne.
Uwaga: Można pokazać, że \(a\) i \(b\) są całkowite – pozostawiamy to jako ćwiczenie dla Czytelnika Wnikliwego.
W szczelnie zamkniętym naczyniu znajduje się \(m = 54\) g pary wodnej w temperaturze \(t_1 = 100\). Ile ciepła należy dostarczyć, aby ogrzać tę parę do \(t_2 = 200\)? Masa atomowa tlenu \(\mu_O = 16,\) masa atomowa wodoru \(\mu_H = 1,\) a uniwersalna stała gazowa \(R = 8{,}314\) J/mol.
Ciało o masie \(m\) porusza się wzdłuż linii prostej \(OX\) pod działaniem siły potencjalnej. Potencjał siły jako funkcja współrzędnej \(x\) opisany jest wzorem: \[U(x) = \frac{a}{x^2} - \frac{b}{x}.\] Jaki jest okres małych drgań ciała wokół położenia równowagi (minimum potencjału)?
