Afiliacja: Wydział Fizyki, Uniwersytet im. Adama Mickiewicza w Poznaniu
W czasach, kiedy jeszcze funkcjonowały gimnazja, na teście końcowym pojawiło się następujące zadanie:
Syrena okrętowa wydaje dźwięk o częstotliwości \(50 \ 1/ \text{s}.\) Oblicz długość emitowanej fali dźwiękowej, przyjmując, że dźwięk rozchodzi się z prędkością \(300 \ \text{m}/\text{s}.\)
Zdarzyło się w pewnej szkole, że uczniowie nie poradzili sobie z tym zadaniem. Usprawiedliwiali się tym, że nauczyciel nie przerobił tematu fal dźwiękowych. Załóżmy więc, że nie wiemy nic o falach dźwiękowych, a jednak nie chcemy dać za wygraną. W treści zadania mamy podane dwie wielkości. Nawet jeśli nie wiemy, jakie literki zwyczajowo oznaczają te wielkości, możemy użyć własnych oznaczeń, np. \(cz=50 \ 1/ \textup{s}\) i \(pr=300 \ \textup{m}/\textup{s}.\) Rozwiązaniem zadania ma być długość – oznaczmy ją literą \(L.\) Jednostką długości jest metr (tę wiedzę powinien przekazać każdy nauczyciel fizyki). Rozważmy teraz cztery próbne rozwiązania. Użyjmy podstawowych działań: \[L_1 = cz+pr,\ \ \ L_2 = cz \cdot pr,\ \ \ L_3 = cz/pr,\ \ \ L_4 = pr/cz.\] W pierwszym przypadku nie bardzo wiemy, jak dodawać \(1/ \textup{s}\) do \(\textup{m}/\textup{s}.\) W drugim przypadku otrzymalibyśmy wynik w \(m/s^2,\) w trzecim w \(1/m,\) a w czwartym w metrach. Wybór czwartej możliwości gwarantuje uzyskanie wyniku z poprawną jednostką. Ponadto wynik \[\nonumber L = pr/cz=6 \ \textup{m}\] okazuje się poprawnym rozwiązaniem, mimo że prowadzące do niego rozumowanie nie było ścisłe. Powyższy przykład wskazuje, że opłaca się zwracać uwagę na jednostki. Zwykle uczniowie nie doceniają nacisku, jaki nauczyciele fizyki kładą na konieczność pamiętania o jednostkach. Jak można obniżać ocenę, myśli uczeń, za taki drobiazg jak podanie końcowego wyniku w formie liczby bez towarzyszącej jej jednostki. A przecież ten drobiazg (w przytłaczającej większości przypadków) powoduje, że odpowiedź pozbawiona jest jakiegokolwiek znaczenia. Każde zadanie z fizyki można przecież zakończyć stwierdzeniem, że wynik wynosi \(1\) – w odpowiednich jednostkach.
Tych, którzy do jednostek podchodzą niefrasobliwie, postraszyć można hiperinflacją: \[\nonumber 1 \ \textup{zł} = 100 \ \textup{gr} = 10 \ \textup{gr} \cdot 10 \ \textup{gr} = 0{,}1 \ \textup{zł} \cdot 0{,}1\ \textup{zł} = 0{,}01\ \textup{zł} = 1 \ \textup{gr}.\] Wracając do naszego zadania, odrzuciliśmy dodawanie \(1/\textup{s}\) i \(\textup{m}/\textup{s},\) ale nie mieliśmy nic przeciwko ich mnożeniu bądź dzieleniu. Jak to możliwe? Rozważmy prostszy przykład. Powierzchnię prostokąta o bokach \(a=1 \ \textup{m}\) i \(b= 2 \ \textup{m}\) obliczamy w następujący sposób: \[\nonumber S= a \cdot b = 1 \ \textup{m} \cdot 2 \ \textup{m}=2 \ \textup{m}^2.{}\] Arytmetyka uczy, że \(1 \cdot 2=2,\) ale co ma oznaczać równanie \(\textup{m} \cdot \textup{m} = \textup{m}^2\)? Gdyby chodziło o wyrażenie algebraiczne, w którym symbol ,,\(\textup{m}\)” zastępuje liczbę, nie byłoby problemu, ale co to znaczy pomnożyć metr razy metr. Warto uświadomić sobie (to główny cel niniejszego artykuliku), że to nic nie znaczy. Symbol \(\textup{m}^2\) nie oznacza mnożenia czegokolwiek, ale jest (sprytnie dobranym tak, aby odwołać się do algebraicznej intuicji) symbolem jednostki powierzchni zwanej metrem kwadratowym. W dawnych czasach umówiliśmy się bowiem za jednostkę powierzchni uznać pole kwadratu o boku \(1\) metra. Ten związek jednostki powierzchni z jednostką długości jest, podkreślmy to raz jeszcze, umowny. Gdyby jakiś chochlik przyjął w dawnych czasach za wzorzec powierzchnię koła o promieniu \(r=1 \ \textup{m},\) to wzór na pole prostokąta wyglądałby dzisiaj tak (biedni uczniowie): \[\nonumber S_{\Box}= \frac{a \cdot b}{\pi}.\]Za to wzór na pole koła uprościłby się do postaci \({S_{\bigcirc}=r^2}.\) Wróćmy do tradycji, w której wzorcem powierzchni jest kwadrat. To pozwala tym samym słowem kwadrat określać zarówno figurę geometryczną \(\square,\) jak i operację mnożenia liczby przez nią samą. Niezależnie od tego, jak zdefiniujemy wzorce długości i powierzchni, pozostaje prawdą (geometryczną czy fizyczną), że powierzchnia obiektu \(S\) skaluje się z kwadratem jego rozmiaru liniowego \(L.\) Zatem relacja \[\label{area} S= A L^2 \tag{1}\] będzie zawsze słuszna, tylko bezwymiarowa stała proporcjonalności \(A\) będzie zmieniać się od przypadku do przypadku. Jeśli rozważymy okrąg o obwodzie \(L,\) to będziemy mieli \(A=1/(4 \pi),\) a jeśli sferę o średnicy \(L,\) to \(A=\pi\) itp. Jeśli zgodzimy się co do tego, że istotne jest skalowanie, a stała proporcjonalności jest drugorzędna, to wiele istotnych związków między wielkościami fizycznymi możemy ustalić, skupiając się na jednostkach. Taką metodę nazywamy analizą wymiarową. Przykładowo spróbujmy ustalić czas spadku swobodnego (pomijamy opory ruchu) obiektu o masie \(m\) z wysokości \(h\) (rys. 1). Wiemy, że istotnym parametrem związanym z rozpatrywanym zjawiskiem jest tzw. przyspieszenie ziemskie \(g.\)
Podobny chochlik zdefiniował kiedyś znak ładunków elektrycznych tak niefortunnie, że pokolenia uczniów muszą mierzyć się z problemem prądu elektrycznego płynącego w kierunku odwrotnym do ruchu elektronów.
Rys. 1
Spodziewamy się zatem następującego wzoru na czas spadku: \[\nonumber t=A \ m^{\alpha} \ h^{\beta} \ g^{\gamma},\] gdzie \(A\) to bezwymiarowa stała (którą uznaliśmy za nieistotną), a \(\alpha, \ \beta, \ \gamma\) to wykładniki, które mamy nadzieję wyznaczyć metodą analizy wymiarowej. Powyższe równanie z punktu widzenia analizy wymiarowej wygląda tak: \[\nonumber \textup{s}= \textup{kg}^{\alpha} \ \textup{m}^{\beta} \ (\textup{m} \ \textup{s}^{-2})^{\gamma},\] a jego spełnienie wymaga, aby \(\alpha=0,\) \(\beta=1/2\) i \(\gamma=-1/2.\) Ostatecznie otrzymujemy prawidłową relację \[\nonumber t=A \sqrt{\frac{h}{g}}.\] A gdybyśmy zapytali o wartość siły, z jaką przyciągają się dwie masy, \(m_1\) i \(m_2,\) znajdujące się w odległości \(r,\) wiedząc, że istotnym parametrem jest stała grawitacji \(G \approx 7 \cdot 10^{-11} \frac{\textup{m}^3}{\textup{kg} \ \textup{s}^2},\) to próbne rozwiązanie miałoby postać: \[\nonumber F=m_1^{\alpha_1} \ m_2^{\alpha_2} \ r^{\beta} \ G^{\gamma}.\] Tym razem pojawia się drobny problem związany z tym, że mając dwie masy, możemy utworzyć wielkość bezwymiarową, np. \(x= \frac{m_2}{m_1}.\) Udziału tej wielkości w ostatecznej formule nie da się ustalić na podstawie analizy wymiarowej. Zapiszmy zatem: \[\nonumber F=f(x) \ m_1^{\alpha_1} \ r^{\beta} \ G^{\gamma},\] gdzie \(f(x)\) jest nieznaną funkcją. Dalej mamy \[\nonumber \textup{kg} \frac{\textup{m}}{\textup{s}^2}=\textup{kg}^{\alpha_1} \ \textup{m}^{\beta} \ \left( \frac{\textup{m}^3}{\textup{kg} \ \textup{s}^2} \right)^{\gamma}.\] Stąd \(\alpha_1 = 2,\) \(\beta=-2\) i \(\gamma=1.\) Ostatecznie (prawie) \[\nonumber F=f(x) \ m_1^2 \ r^{-2} \ G.{}\]
Warunek symetrii implikuje, że funkcja \(f\) musi spełniać równanie \[f(x)=f(1/x)x^2.\] Jeżeli ograniczymy się do funkcji postaci \(f(x)=x^\kappa,\) to rzeczywiście jedynym rozwiązaniem jest \(\kappa=1,\) czyli \(f(x)=x.\) Zachęcamy Czytelnika do zastanowienia się nad znalezieniem innych rozwiązań powyższego równania (bez ograniczania się do funkcji potęgowych) i ich interpretacji.
Jeśli dodatkowo odwołamy się do symetrii powiązanej z III zasadą dynamiki, to uznamy, że \(f(x)=x,\) i otrzymamy znany wzór: \[\nonumber F=G \ \frac{m_1 \cdot m_2}{r^2}.\] Wydawać by się mogło, że korzystając z analizy wymiarowej, ,,wyprowadziliśmy” prawo grawitacji. Czyż nasza mądrość osiągnęła poziom Newtona? Niestety nie jest aż tak dobrze, nasz sukces związany jest z użyciem stałej grawitacji. To w niej (zwłaszcza w jej jednostce) zaszyta jest istotna informacja dotycząca grawitacji. Otrzymaliśmy tę informację w prezencie i ją wykorzystaliśmy. Sprytne wykorzystanie dostępnej informacji nie jest rzeczą wstydliwą. To część warsztatu fizyka. Sukces analizy wymiarowej oparty jest na umiejętności wyizolowania wielkości, które są istotne z punktu widzenia rozpatrywanego zagadnienia. To nie jest łatwa umiejętność, nabywa się ją wraz z doświadczeniem. I chociaż wiąże się to z wysiłkiem, to gorąco zachęcam do ćwiczenia tej umiejętności najpierw w zagadnieniach, które potrafimy rozwiązać ściśle, a następnie tam, gdzie inne metody zawodzą.
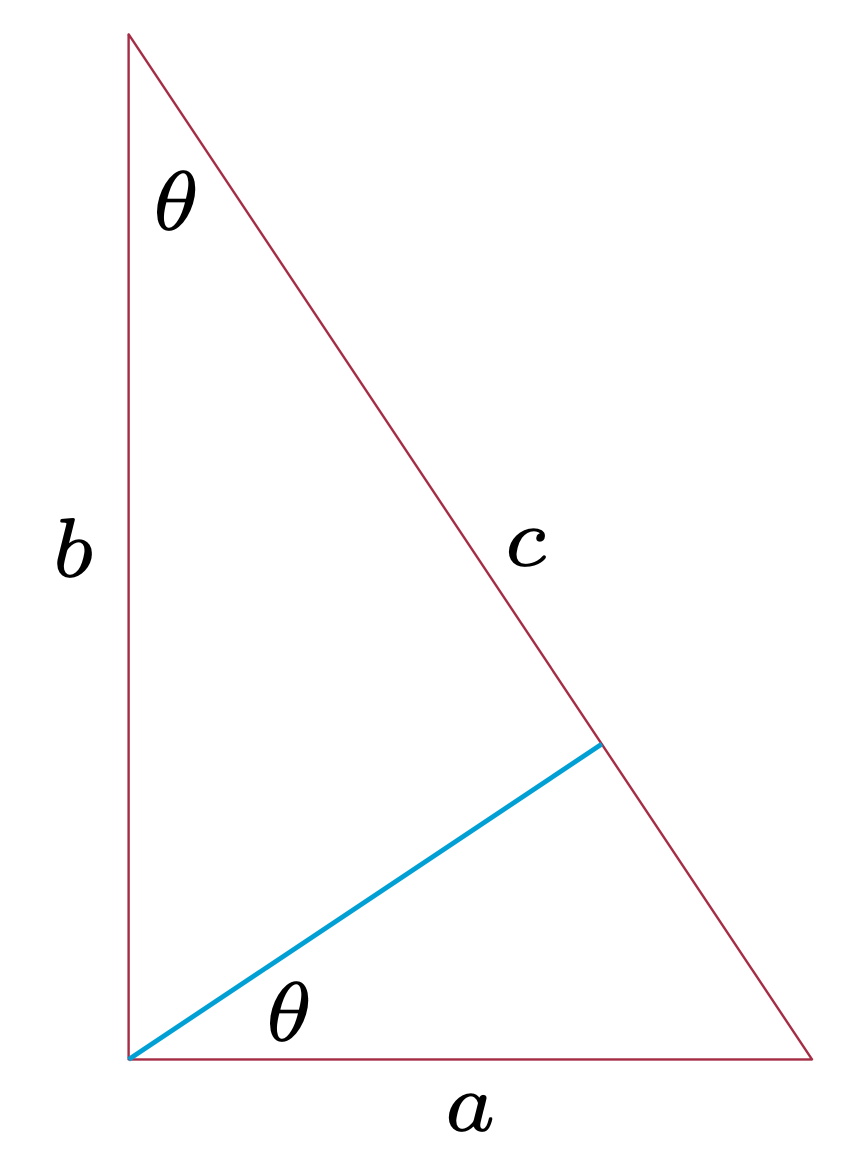
Co ciekawe, analiza wymiarowa może przydać się również w problemach czysto matematycznych. Załóżmy, że słabo radzimy sobie z rachunkiem całkowym. Otrzymaliśmy informację, że \[\nonumber \int\nolimits_{-\infty}^{\infty} e^{-x^2} dx=\sqrt{\pi},\] i zadanie wyznaczenia \[\int\nolimits_{-\infty}^{\infty} e^{-\frac{x^2}{4}} dx.\] Przyjmijmy (roboczo), że \(x\) jest wielkością mierzoną w metrach. Wtedy szukana całka musi też być wyrażona w metrach. Z kolei wykładnik musi być bezwymiarowy, a to znaczy, że \(4\) to dla nas \(4 \ \textup{m}^2.\) Żeby uzyskać z tej wielkości wartość mierzoną w metrach, należy użyć pierwiastka. Po ustaleniu tej zależności możemy zapomnieć o metrach i zapisać rozwiązanie w postaci \[\nonumber \int\nolimits_{-\infty}^{\infty} e^{-\frac{x^2}{4}} dx=\sqrt{4 \ \pi}.\] Inny (matematyczny) przykład wiąże się z możliwością dowiedzenia twierdzenia Pitagorasa na podstawie zamieszczonego rysunku przedstawiającego trzy trójkąty prostokątne. Zastosujmy wynikające z analizy wymiarowej równanie \(\eqref{area}\) do trójkąta prostokątnego. Niech \(L\) oznacza długość przeciwprostokątnej, a bezwymiarowa stała niech będzie równa nieznanej funkcji najmniejszego kąta w trójkącie \(A=f(\theta).\) Z rysunku 2 wynika, że pole dużego trójkąta jest równe sumie pól trójkątów mniejszych. Możemy to wyrazić równaniem \[\nonumber f(\theta) \cdot c^2= f(\theta) \cdot a^2+f(\theta) \cdot b^2,\] z którego twierdzenie Pitagorasa wynika bezpośrednio (\(f(\theta)\neq 0\)).
Rys. 2
Na koniec chciałbym zachęcić Cię, Czytelniku, do samodzielnego zmierzenia się z dwoma problemami.
Typowym i bardzo pouczającym przykładem jest zagadnienie oporów ruchu w powietrzu (tych, które pomijaliśmy w przykładzie spadku swobodnego). Jako istotne wielkości proszę przyjąć rozmiar obiektu (\(\textup{m}\)), jego prędkość (\(\frac{\textup{m}}{\textup{s}}\)) oraz gęstość (\(\frac{\textup{kg}}{\textup{m}^3}\)) i lepkość (\(\frac{\textup{kg}}{\textup{m} \cdot \textup{s}}\)) powietrza. Warto rozpatrzyć trzy przypadki. W przypadku ogólnym powinno się zaobserwować bezwymiarową kombinację wspomnianych czterech wielkości. Zbadaj również dwa przypadki graniczne – jeden, w którym zaniedbuje się lepkość, i drugi, w którym zaniedbuje się gęstość powietrza.
O analizie wymiarowej pisał również Jan Kalinowski w \(\Delta^4_{17}.\)
Kolejne pouczające ćwiczenie polega na wyznaczeniu za pomocą analizy wymiarowej trzech wielkości – o wymiarze masy, długości i czasu, z wykorzystaniem trzech stałych – stałej grawitacji, stałej Plancka i prędkości światła w próżni. Tak wyznaczone wielkości nazywamy masą Plancka, długością Plancka i czasem Plancka. Porównaj, Czytelniku, wyznaczone wielkości z typowymi wielkościami skali atomowej – \(m=10^{-27} \ \textup{kg},\) \(L=10^{-10} \ \textup{m}\) i \({t=10^{-15} \ \textup{s}}.\) Co zwróciło Twoją uwagę?