W pewnym kraju znajduje się \(N\) miast. Należy połączyć je liniami kolejowymi tak, by łączna długość linii kolejowych była możliwie najmniejsza. Miasta mogą być węzłami kolejowymi, w których zbiegają się linie, można także budować węzły kolejowe poza miastami.
Przedstawione zadanie jest jednym z możliwych sformułowań tzw. problemu drzewa Steinera. Jest to problem NP-trudny. Co ciekawe, lepiej i szybciej niż na komputerze można go rozwiązywać, przeprowadzając eksperymenty fizyczne.
Na czym polega odpowiedni eksperyment, wie każdy, kto kiedykolwiek puszczał bańki mydlane. Ze względu na istnienie napięcia powierzchniowego warstewka wody z mydłem rozpięta na zakrzywionej pętli przybiera kształt minimalizujący powierzchnię. Do rozwiązania problemu drzewa Steinera wystarczy więc wziąć pleksiglasową płytę, wbić w odpowiednie miejsca kołki i całość zanurzyć w wiadrze z mydlinami. Wyjmując, dobrze jest trochę potrząsać układem, a fizyka sama już ustali połączenia kołków błoną mydlaną o najmniejszej powierzchni, a więc, jeśli patrzeć z kierunku prostopadłego do płyty, połączy wybrane punkty liniami o minimalnej sumie długości krawędzi.
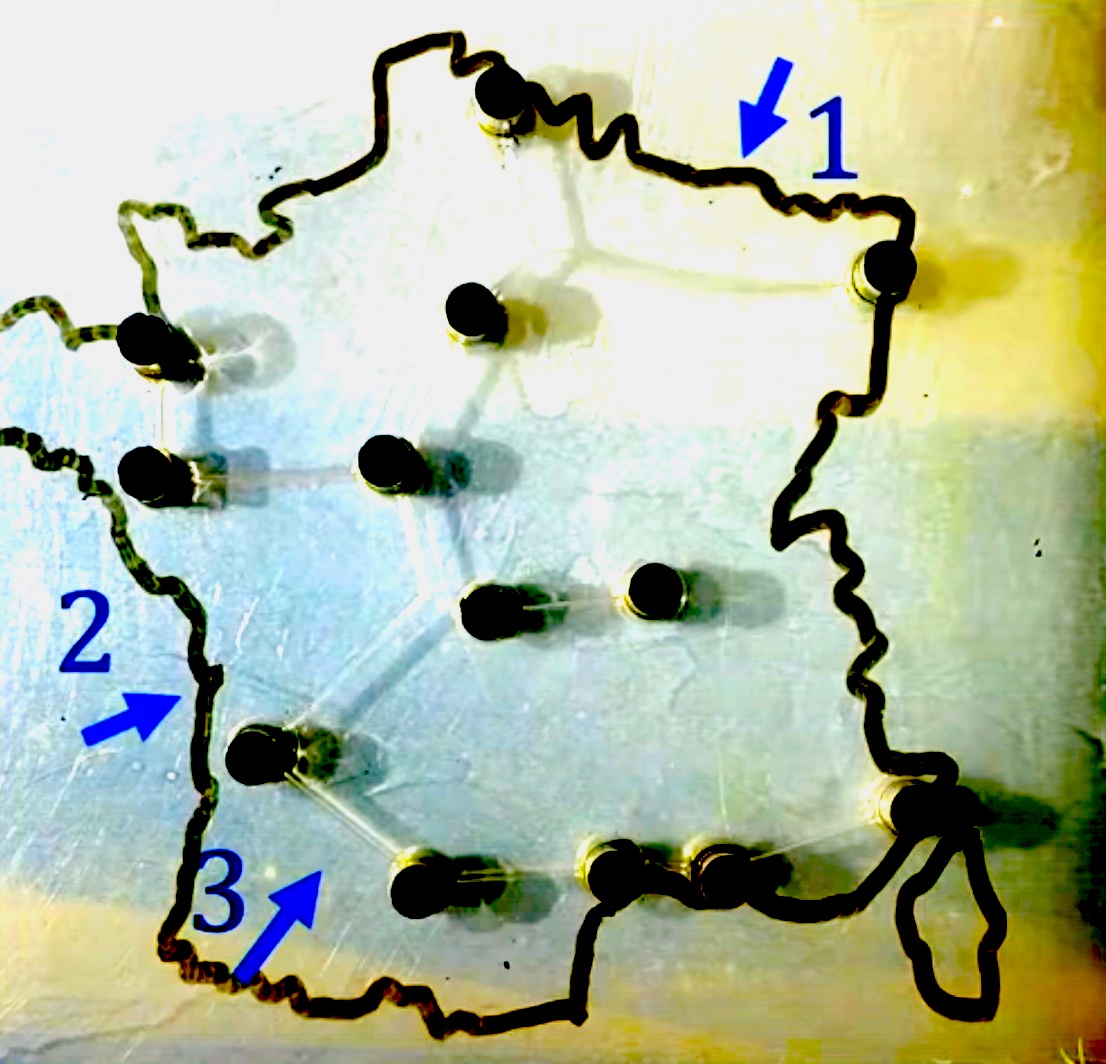
Takie właśnie doświadczenie przedstawiła drużyna z École Polytechnique, reprezentująca Francję, na odbywających się w kwietniu w Zurychu zawodach 16. Międzynarodowego Turnieju Fizyków. Dzięki odpowiedniemu doborowi składu chemicznego substancji zawodnicy byli w stanie tworzyć elastyczne i trwałe błonki. Popisowym elementem rozwiązania problemu drzewa Steinera dla \(N=13\) było zaproponowanie najkrótszej sieci kolejowej łączącej trzynaście największych miast Francji. Algorytmowi komputerowemu znalezienie rozwiązania zajęło około trzech minut. Włożenie odpowiedniej płytki do wiadra z wodą i chwila potrząsania – zaledwie pół minuty.
Jeżeli umieścić kołki między dwiema pleksiglasowymi płytami, których odległość nie jest stała, gdyż są względem siebie nachylone albo ich powierzchnia nie jest płaska, można rozwiązywać inne problemy optymalizacyjne. Dla płyt nachylonych szerokość błonki zmienia się liniowo w zależności od położenia – dokładnie tak samo jak energia stałego i jednorodnego pola grawitacyjnego. W takich warunkach dwa kołki będą połączone krzywą łańcuchową, czyli kształtem, jaki przybiera, zwisając, lina zaczepiona na końcach.
Opisane wyżej doświadczenia są dość typowe dla rozwiązań przedstawianych na Międzynarodowym Turnieju Fizyków. Ogłaszane z wyprzedzeniem zadania mają charakter półotwarty – to do rozwiązującego należy określenie, co i jak należy zbadać, a doświadczenia mieszają zazwyczaj elementy fizyki ,,kuchennej” i zaawansowanych badań naukowych. Rozwiązania zadań są publicznie dyskutowane na scenie. Rolą oponenta (z innej drużyny) jest wskazanie możliwych ulepszeń rozwiązania podczas dyskusji koordynowanej przez moderatora (z jeszcze innej drużyny). Za poziom wykonania każdej z ról międzynarodowe jury przyznaje punkty, które z odpowiednimi wagami liczą się w ogólnej klasyfikacji Turnieju.
W tegorocznej edycji Turnieju brały też udział drużyny z Polski, z Uniwersytetu Warszawskiego i z Uniwersytetu Jagiellońskiego, które zajęły, odpowiednio, piąte i dziewiętnaste miejsce. Każda uczelnia może zgłosić swoją drużynę do rozgrywek, a kto weźmie udział w zawodach międzynarodowych, ustalane jest w trakcie eliminacji krajowych, które organizowane są przez przedstawiciela krajowego. W Polsce jest nim autor niniejszego tekstu, który gorąco zaprasza do udziału. Naprawdę warto!
Zdjęcia pochodzą z prezentacji drużyny École Polytechnique przedstawionej podczas finału 16. Międzynarodowego Turnieju Fizyków. Nagranie finałowej potyczki dostępne jest w serwisie YouTube pod adresem https://www.youtube.com/live/vl3kmfSo-ws?si=9lNHSGAv9cX7PjK4