Afiliacja: Centrum Fizyki Teoretycznej, Polska Akademia Nauk
Ogólna teoria względności (1916) Alberta Einsteina jest jedną z najbardziej fascynujących teorii w historii nauki. Wyjaśnia nie tylko naturę siły grawitacji jako geometrycznej cechy czasoprzestrzeni, ale także zawiera zdumiewające przewidywania dotyczące egzotycznych obiektów fizycznych i zjawisk, takich jak czarne dziury, a nawet napędy warp, znane z dzieł science fiction.
Zgodnie z przewidywaniami ogólnej teorii względności wszelkie łączące się masywne obiekty, takie jak czarne dziury i gwiazdy neutronowe, wytwarzają fale grawitacyjne, jeśli tylko układ ich mas porusza się z przyspieszeniem i zmienia swój całkowity moment kwadrupolowy. W teorii Einsteina fale grawitacyjne rozchodzą się z prędkością światła, co zostało potwierdzone obserwacją zjawiska GW170817 z 2017 roku. Kiedy fala grawitacyjna dociera do obiektu, ściska go i rozciąga w określonych kierunkach. Innymi słowy – odległość między punktami zmienia się. Zmiany te są jednak tak niewielkie, że wykrywanie ich było ogromnym wyzwaniem inżynieryjnym: technika dokładnych pomiarów musiała znacznie się rozwinąć, aby było można stworzyć urządzenie zdolne do pomiaru tak małych różnic odległości.
Podobnie do promieniowania elektromagnetycznego, w którym promieniowanie jest wynikiem przyspieszonego ruchu ładunków elektrycznych, fale grawitacyjne powstają, gdy masy poruszają się z przyspieszeniem. W związku z prawami zachowania masy-energii oraz pędu promieniowanie grawitacyjne jest co najmniej kwadrupolowe (promieniowanie elektromagnetyczne może być dipolowe, ponieważ w tym przypadku mamy jedynie prawo zachowania ładunku elektrycznego).
Wśród pomysłodawców pierwszego detektora fal byli Mikhail Gertsenshtein, Vladislav Pustovoit, Rainer Weiss – późniejszy autor sukcesu LIGO – oraz Joseph Weber, który jest słynny z powodu innego typu detektorów fal grawitacyjnych, tzw. walców rezonacyjnych.
Charakterystyka sygnału została niedawno opisana przez Luke’a Sellersa i współautorów w pracy
arXiv:2212.02065; nazywają oni napęd warp akronimem RAMAcraft (ang. Rapid And/or Massive Accelerating spacecraft).
W latach 60. powstały pierwsze pomysły zbudowania interferometru laserowego do wykrywania fal grawitacyjnych. Detektor ma dwa, najczęściej prostopadłe, ramiona, każde o długości \(L\) rzędu kilku kilometrów. Fotony światła laserowego przemieszczają się wewnątrz ramion detektora i są odbijane przez lustra na ich końcach. Kiedy fala przechodzi przez detektor, odległości w ramionach zmieniają się (bardzo niewiele, około \(10^{-18}\) m, czyli znacznie mniej niż rozmiar protonu), a zmiany te powodują zmiany obrazu interferometrycznego wiązek laserowych, które spotykają się w punkcie centralnym interferometru. Względna zmiana długości ramienia, \(h=\Delta L/L,\) jest mierzoną amplitudą fali grawitacyjnej. Pierwszy sygnał został wykryty we wrześniu 2015 roku przez LIGO (Laser Interferometer Gravitational-Wave Observatory). Pochodził on z dwóch łączących się czarnych dziur znajdujących się w odległości 400 Mpc od Ziemi. Od tego czasu detektory LIGO i Virgo wykryły ponad 100 sygnałów z różnych układów podwójnych, zawierających czarne dziury o różnych masach oraz gwiazdy neutronowe. Wykrycie fal grawitacyjnych jest z pewnością wielkim osiągnięciem, ale co ważniejsze, możliwość ich detekcji daje nowe narzędzie do obserwacji Wszechświata.
Układy podwójne nie są oczywiście jedynym źródłem fal grawitacyjnych. Oprócz badania zjawisk naturalnych detektory fal grawitacyjnych mogą pomóc nam w poszukiwaniu pozaziemskiej inteligencji. Zgodnie z teorią względności fale grawitacyjne mogą być generowane przez wspomniane na wstępie napędy warp. Sygnał byłby wynikiem zaawansowanego mechanizmu transportowego i wiązałby się z faktem, że układ mas poruszających się z przyspieszeniem wytwarza fale grawitacyjne: jeśli statek kosmiczny byłby masywny i znajdowałby się wystarczająco blisko nas, moglibyśmy go wykryć, gdy przyspiesza.
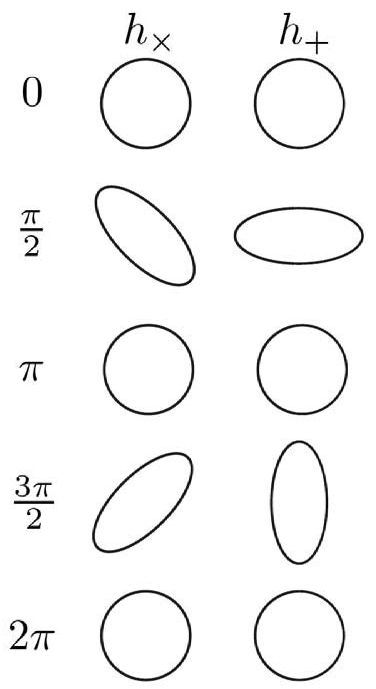
Podobnie jak fale elektromagnetyczne, fale grawitacyjne mogą być spolaryzowane na dwa sposoby: \(h_+\) i \(h_\times.\) Można sobie wyobrazić spolaryzowaną falę \(h_+\) poruszającą się w kierunku prostopadłym do płaszczyzny, w którym znajduje się płaski, kołowy rozkład mas testowych. Fala \(h_+\) naprzemiennie rozciąga i ściska rozkład mas; fala spolaryzowana wyłącznie w polaryzacji \(h_\times\) robi to samo, ale pod kątem 45\(^\circ.\) Aby wykryć falę, musimy obliczyć składowe \(h_+\) i \(h_\times\) w celu określenia, jak silnie czasoprzestrzeń jest zaburzana przez falę grawitacyjną nadchodzącą z określonego kierunku i odległości. Następnie przeszukujemy dane obserwacyjne, używając zbioru ,,szablonów” (modeli) fal grawitacyjnych, które przewidujemy dla różnych źródeł o określonych parametrach.
Historia wygląda tak samo w przypadku przyspieszającego statku kosmicznego. Wyobraźmy sobie, że porusza się on ze stałym przyspieszeniem wzdłuż osi \(z,\) masa statku kosmicznego nie zmienia się znacząco, a fale są emitowane w płaszczyźnie prostopadłej do kierunku ruchu (np. są spolaryzowane polaryzacją \(h_+\)). Przyjmując te założenia i wykonując pewne obliczenia matematyczne w ogólnej teorii względności, a następnie stosując zasady fizyki Newtona, takie jak zachowanie masy i pędu oraz trzecie prawo Newtona, otrzymamy \[h = \tfrac{4GM}{Rc^4}v(t)^2,\] gdzie \(h\) jest bezwymiarową wielkością reprezentującą odkształcenie czasoprzestrzeni pod wpływem fali grawitacyjnej (obserwowane wielkości byłyby rzędu \(10^{-21}\) lub mniejsze). Parametr \(M\) to masa statku kosmicznego, \(G\) to stała grawitacyjna, \(c\) to prędkość światła, \(R\) to odległość między źródłem a detektorem i wreszcie \(v(t)\) to prędkość statku kosmicznego, która zmienia się w czasie: im masywniejsze źródło i im bliżej się znajduje, tym silniejszy sygnał.
Przykładowa zmiana amplitudy fali grawitacyjnej podczas przyspieszonego ruchu statku kosmicznego
Załóżmy, że obiekt ma prędkość początkową \(v_0\) i podlega stałemu przyspieszeniu \(A,\) począwszy od \(t=0,\) przez okres \(T.\) W wyniku otrzymamy równanie na amplitudę fali \(h\) zależną od czasu i przyspieszenia: \[h = \begin{cases} \frac{4GM}{Rc^4}v_0^2 & t < 0 ,\\ \frac{4GM}{Rc^4}(At+v_0)^2 & 0 < t < T. \\ \end{cases}\] Zakładając, że cały czas przyspieszenia jest objęty czasem obserwacji, można wykazać, że sygnały te mogą być wykrywane przez współczesne detektory. Interferometry LIGO lub Virgo mogą wykrywać sygnały w szerokim zakresie częstotliwości od 10 Hz do \(10^4\) Hz. Załóżmy, że czas obserwacji to około 5 minut, a czas przyspieszania to 10 sekund, i wybieramy energię kinetyczną statku kosmicznego w zakresie od \(10^{-9}M_{\odot}c^2\) do \(0{,}25 M_{\odot}c^2\) (czyli od statku kosmicznego o ,,normalnych rozmiarach” aż po gigantyczny obiekt o masie Słońca osiągający prędkości relatywistyczne).
Podstawowe równanie dotyczące związku zmiany prędkości \(v\) ze stałym przyspieszeniem \(A\) w czasie \(t\) od 0 do \(T\) to oczywiście \(v(t) = At+v_0.\)
W ogólnej teorii względności, w słabym polu grawitacyjnym, metryka \(g_{\mu\nu},\) która opisuje zakrzywienie czasoprzestrzeni, może być zapisana jako metryka przestrzeni płaskiej \(\eta_{\mu\nu}\) i metryka opisująca perturbację \(h_{\mu\nu},\) czyli \(g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}.\) Układ fizyczny powinien mieć niezerowy moment kwadrupolowy, aby emitować fale grawitacyjne. Jeśli zapiszemy równania teorii dla odległej, wolno poruszającej się materii, otrzymamy wzór na moment kwadrupolowy: \(h_{ij} = \frac{2G}{Rc^4}\frac{d^2 I_{ij}}{dt^2},\) gdzie \(I_{ij}\) jest kwadrupolowym momentem rozkładu masy. Dla punktowej masy poruszającej się wzdłuż osi \(z\) można pokazać, że wszystkie składowe \(I_{ij}\) są zerowe z wyjątkiem \(I_{zz} = M(t)z^2(t).\) W ogólnym przypadku, w którym masa statku kosmicznego zmienia się, mamy: \({h}_{zz} =\)
\(=\frac{2G}{Rc^4}\left(2M\dot{z}^2 +4\dot{M}z\dot{z}+2Mz\ddot{z} + \ddot{M}z^2\right),\) gdzie kropka oznacza różniczkowanie względem czasu \(t\) w układzie detektora. W głównym tekście przyjęliśmy upraszczające założenie, że odrzut i jego masa są zaniedbywane. Po zastosowaniu tego założenia i zasady zachowania masy, pędu i trzeciego prawa Newtona dostaniemy wzór wyróżniony w tekście.
Przy takich założeniach okazuje się, że np. statek kosmiczny o masie \(\sim 10^{-2} M_{\odot}\) (10 mas Jowisza) zmieniający prędkość o \(0{,}1c\) emitowałby fale grawitacyjne wykrywalne do odległości \(10^5\)–\(10^6\) pc od Ziemi, czyli mniej więcej takiej, jaka dzieli nas od galaktyki Andromedy. Na dolnym końcu zakresu widzimy, że masy w skali Merkurego \(\sim 10^{-7} M_{\odot}\) przechodzące tę samą zmianę prędkości są wykrywalne do 1–10 pc, czyli w okolicy gwiezdnego otoczenia Układu Słonecznego (odległość do najbliższej gwiazdy, Proxima Centauri, to 1,3 pc).
Masa statku kosmicznego zwiększa się zgodnie z teorią względności. Na przykład statek o masie spoczynkowej \(10^{-3} M_{\odot}\) będzie miał relatywistyczną masę \(M= M_0/\sqrt{1-v^2/c^2} \sim 1{,}33\times 10^{-3} M_{\odot},\) gdy porusza się z prędkością 0,5 \(c.\) Energia równoważna tej dodatkowej masie wynosi \(0{,}00033 M_{\odot}c^2 \sim 6\times 10^{43}\) J: jest jasne, że Obcy potrzebują zaawansowanych technologicznie silników, aby przyspieszyć swój statek kosmiczny do tej prędkości.
Dotychczas obserwatoria LIGO i Virgo nie wykryły żadnego silnego sygnału tego typu, a zatem można zaryzykować stwierdzenie, że w ciągu ostatnich kilku lat w naszej Galaktyce nie było przyspieszającego statku kosmicznego o masie porównywalnej do masy Jowisza. Jednak rozwijając metodologię, poprawiając czułość detektorów, być może już wkrótce, gdy na odległej planecie Obcy uruchomią silniki swojego statku kosmicznego, będziemy w stanie je usłyszeć.
Tłumaczenie: Michał BEJGER