Afiliacja: Uczennica, XIV LO im. Stanisława Staszica w Warszawie oraz Doktorant, Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Wyszukiwanie binarne to algorytm służący do odnalezienia określonego elementu w posortowanej tablicy. Jego zaletą jest to, że umożliwia znalezienie elementu w znacznie krótszym czasie niż w przypadku tradycyjnego przeszukiwania tablicy, polegającego na ,,przechodzeniu” po niej element po elemencie i porównywaniu napotykanych elementów z szukanym.
Załóżmy, że dana jest posortowana tablica \([a_0, a_1, \ldots, a_{n - 1}], a_0 \le a_1 \le \ldots \le a_{n - 1}\) oraz pewna wartość \(x.\) Celem algorytmu wyszukiwania binarnego jest znalezienie pozycji elementu o wartości \(x\) albo stwierdzenie, że ten element nie pojawia się w tablicy (wówczas algorytm zwraca \(-1\)).
Przykładem może być tablica liczb \(T = [3, 4, 4, 10, 11, 17, 18, 19, 21],\) dla której chcemy sprawdzić, czy zawiera element \(x=17.\) Algorytm wyszukiwania binarnego działa w następujący sposób. Rozpoczynamy od wybrania elementu w środku tablicy – wśród wartości \([a_0, a_1, \ldots, a_8]\) tym elementem jest \(a_4 = 11\) (pozycje w tablicy indeksujemy od \(0\)). Następnie porównujemy ten element z wartością \(17.\) Ponieważ \(11\) jest mniejsze od \(17,\) to szukany element na pewno nie znajduje się w lewej połowie tablicy – jeśli jest w tablicy, to będzie w jej prawej części. W kolejnym kroku ograniczamy się więc tylko do prawej połowy \([a_5, a_6, a_7, a_8]\) – jej środkowym elementem jest \(a_6 = 18\) (równie dobrze moglibyśmy wziąć \(a_7,\) ponieważ tablica, do której się ograniczyliśmy, ma parzystą liczbę elementów). Porównując go z \(17,\) stwierdzamy, że musimy szukać w lewej części prawej połowy. Wówczas zostaje nam tylko element \(a_5=17,\) czyli nasz \(x\) jest w tablicy na pozycji \(5.\)
Zauważmy, że podobne podejście często stosujemy intuicyjnie, na przykład przy wyszukiwaniu słowa w słowniku. Mając do znalezienia słowo Delta, nie zaczynamy przeglądać słownika od pierwszej strony wyraz po wyrazie, tylko otwieramy go we w miarę losowym miejscu, patrzymy, jakie wyrazy się tam znajdują, a z tego już wiemy, czy Delta jest na wcześniejszych, czy na dalszych stronach.
Algorytm wyszukiwania binarnego można zapisać w postaci pseudokodu następująco:
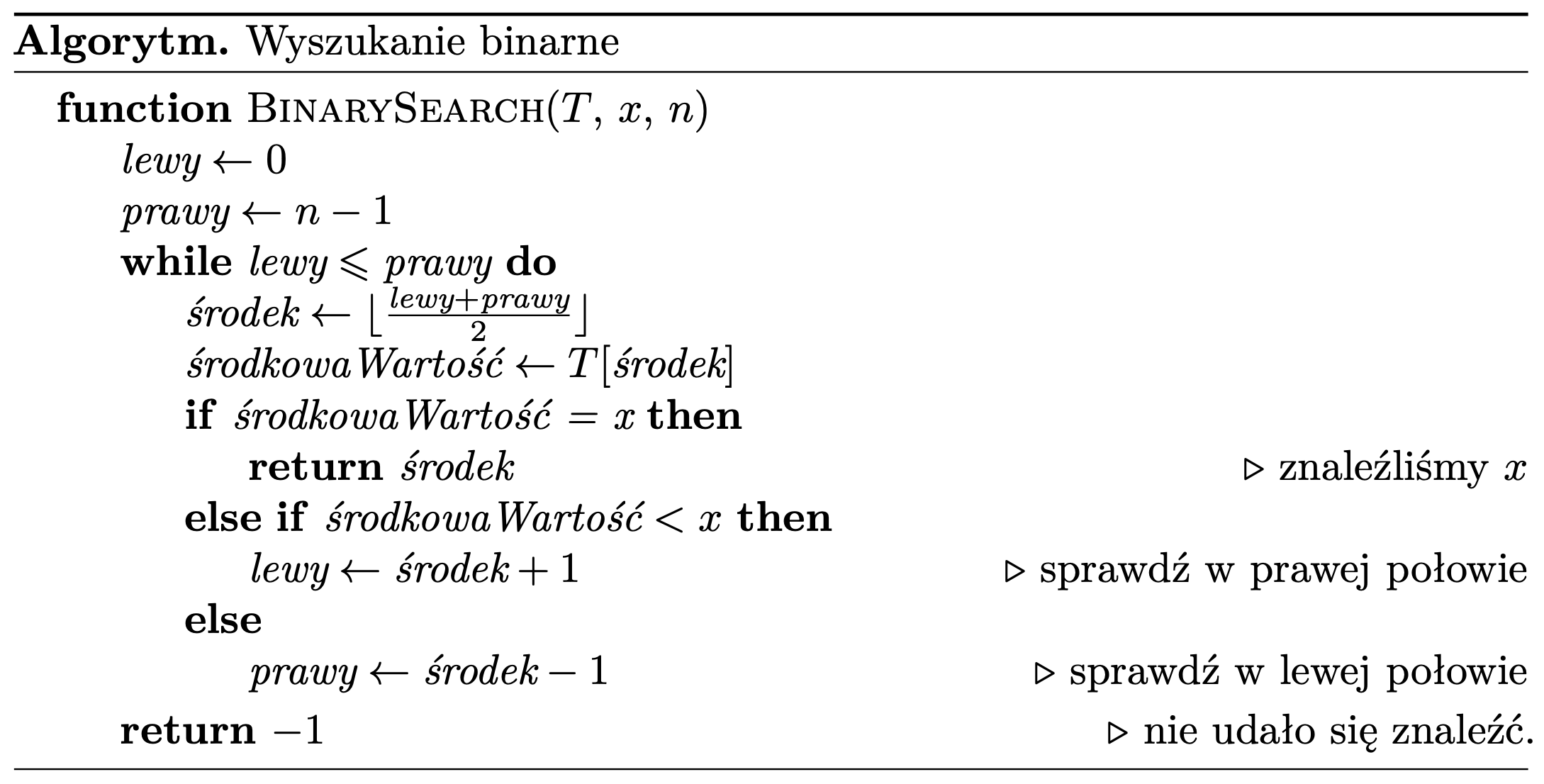
Tak jak zauważyliśmy w przykładzie, porównując jakiś element \(a_i\) z szukaną wartością \(x,\) dowiadujemy się, czy szukany element jest na lewo, czy na prawo od \(a_i.\) Pozwala to w każdym kroku wyeliminować połowę elementów tablicy, a więc otrzymujemy złożoność czasową \(O(\log n).\) Tradycyjne przeszukiwanie tablicy, przeglądające ją element po elemencie, w najgorszym przypadku może wymagać aż \(O(n)\) porównań.
Intuicyjnie jest jasne, że wyszukiwanie binarne działa poprawnie. Formalne udowodnienie poprawności algorytmu wyszukiwania binarnego wymaga jednak odwołania się do pojęć takich jak ,,niezmiennik pętli”, ale w tym krótkim artykule nie będziemy o nich mówić.
Przykładem wykorzystania wyszukiwania binarnego jest zadanie ,,Wieża”, które pochodzi z Obozu Naukowego PROSERWY 2010, a jego autorem jest Jacek Tomasiewicz.
Zadanie ,,Wieża”: W Bajtocji wybudowano wysoką wieżę. Wejście na wieżę składa się z \(m\) schodków, a każdy schodek ma pewną wysokość. Bajtocką wieżę chce odwiedzić \(n\) mieszkańców. To, czy dana osoba jest w stanie pokonać kolejne schodki, zależy od jej wzrostu. Aby mieszkaniec Bajtocji mógł wejść na pewien schodek, musi być wyższy od schodka. Jeśli pewien schodek jest nie do przejścia przez mieszkańca, to zatrzymuje się on w danym miejscu na wieży – wyżej nie będzie mógł wejść. Znając wysokości kolejnych schodków i osób zwiedzających wieżę, chcielibyśmy wiedzieć, w którym miejscu zatrzyma się każdy mieszkaniec Bajtocji.
Zachęcamy Czytelnika do próby samodzielnego rozwiązania powyższego zadania przed przeczytaniem naszego rozwiązania.
Rozwiązanie: Aby rozwiązać zadanie, dla każdego schodka \(s\) najpierw obliczymy wysokość najwyższego schodka leżącego na drodze od spodu wieży do samego \(s\) (np. dla kolejnych wysokości schodków \(1, 5, 3, 6, 2, 1, 7\) stworzymy ciąg \(1, 5, 5, 6, 6, 6, 7).\) W tym celu przechodzimy tablicę od pierwszego do ostatniego elementu, co krok aktualizując największą znalezioną dotychczas liczbę poprzez porównanie jej z wysokością aktualnego schodka. Otrzymujemy w ten sposób w czasie \(O(m)\) niemalejący ciąg. Zauważmy, że mieszkaniec o wzroście \(h\) wejdzie na schodek \(s\) tylko wtedy, gdy najwyższy schodek na drodze od spodu wieży do \(s\) jest niższy niż \(h.\) W związku z tym dla każdego mieszkańca możemy w czasie \(O(\log m)\) znaleźć miejsce, w którym się on zatrzyma – będzie to pierwszy schodek nie niższy od jego wzrostu. Całe rozwiązanie działa więc w czasie \(O(m + n\log m).\)
