Renesans słów Lyndona

* Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski

Redaktor Delty w latach 2009–2014.

W artykule pt. Słowa pierwsze opublikowanym w \(\Delta^{12}_{10}\) opisałem różne własności słów Lyndona. Żeby przypomnieć, czym są słowa Lyndona, trzeba podać kilka definicji dotyczących słów (skończonych). Rotacja słowa, zwana też obrotem cyklicznym, polega na przerzuceniu dowolnej (potencjalnie zerowej) liczby liter z początku słowa na koniec. Na słowach określa się porządek leksykograficzny , czyli słownikowy. I teraz słowem Lyndona nazywamy słowo, które jest ściśle najmniejsze w porządku leksykograficznym wśród swoich rotacji. Przykładowo słowo aaab jest słowem Lyndona, ponieważ wszystkie jego pozostałe rotacje, aaba, abaa i baaa, są od niego większe leksykograficznie. Innymi przykładami słów Lyndona są aabab i a. Natomiast słowo abaaab nie jest słowem Lyndona, gdyż jego rotacja aaabab jest mniejsza leksykograficznie od niego. Również słowo aabaab nie jest słowem Lyndona, jako że jego rotacja o 3 litery jest mu równa. Równoważna definicja słów Lyndona jest taka, że słowa Lyndona są mniejsze od wszystkich swoich właściwych sufiksów (czyli końcowych fragmentów).

Mówimy, że słowo \(u\) jest mniejsze leksykograficznie niż słowo \(v\), jeśli albo słowo \(u\) jest właściwym prefiksem (czyli początkowym fragmentem) słowa \(v\), albo na pierwszej pozycji, na której słowa \(u\) i \(v\) różnią się, w słowie \(u\) występuje litera mniejsza niż w słowie \(v.\)

Słowa Lyndona nazywa się także słowami pierwszymi, przez analogię do liczb pierwszych; tak jak każda liczba naturalna przedstawia się jednoznacznie (z dokładnością do kolejności) jako iloczyn liczb pierwszych, tak każde słowo przedstawia się jednoznacznie jako sklejenie nierosnącego (leksykograficznie) ciągu słów Lyndona. Przykładowo słowo abaababaabaaba jest sklejeniem słów Lyndona ab aabab aab aab a. Dowód tej własności znalazł się we wspomnianym artykule wraz z innymi podstawowymi faktami dotyczącymi słów Lyndona oraz ich zadziwiającym związkiem z ciągami de Bruijna.

Po lekturze numeru \(\Delta^{12}_{10}\) Czytelnik mógł przekonać się, że słowa Lyndona są perełką kombinatoryki słów. Natomiast pewnie mało kto mógł przewidzieć, że w ciągu kolejnych lat staną się one jednym z kluczowych narzędzi zarówno w tej dziedzinie, jak i w algorytmach tekstowych, a algorytmy bazujące na nich będą miały istotne zastosowania praktyczne. W tym artykule opowiem o dwóch takich zastosowaniach słów Lyndona.

Pierwsze z nich dotyczy pojęcia maksymalnych okresowości (ang. runs) w słowie. Do ich zdefiniowania znów potrzebnych jest kilka pojęć. Potęgą słowa \(w\) o wykładniku \(m\), oznaczaną \(w^m\), nazywamy sklejenie kolejno \(m\) kopii słowa \(w\). Powiemy, że słowo \(s\) ma okres \(p\), jeśli \(s\) jest prefiksem potęgi \(w^m\) dla pewnego słowa \(w\) o długości \(p\). Jako \(p\) wybieramy zazwyczaj najmniejszy okres słowa. Jeśli okres \(p\) jest co najmniej dwa razy mniejszy niż długość słowa \(s\), powiemy, że słowo \(s\) jest okresowe. Przykładowo, słowo \(\texttt{abcabcabcab}\) jest okresowe z okresem 3, ponieważ jest prefiksem słowa \((\texttt{abc})^4\). Okresowością w słowie \(s\) nazwiemy dowolny spójny fragment słowa \(s\), który jest okresowy. Wreszcie okresowość nazwiemy maksymalną, jeśli nie da się jej rozszerzyć o jedną pozycję (ani w lewo, ani w prawo) z zachowaniem jej (najkrótszego) okresu. Wszystkie maksymalne okresowości w przykładowym słowie można znaleźć na poniższym rysunku:

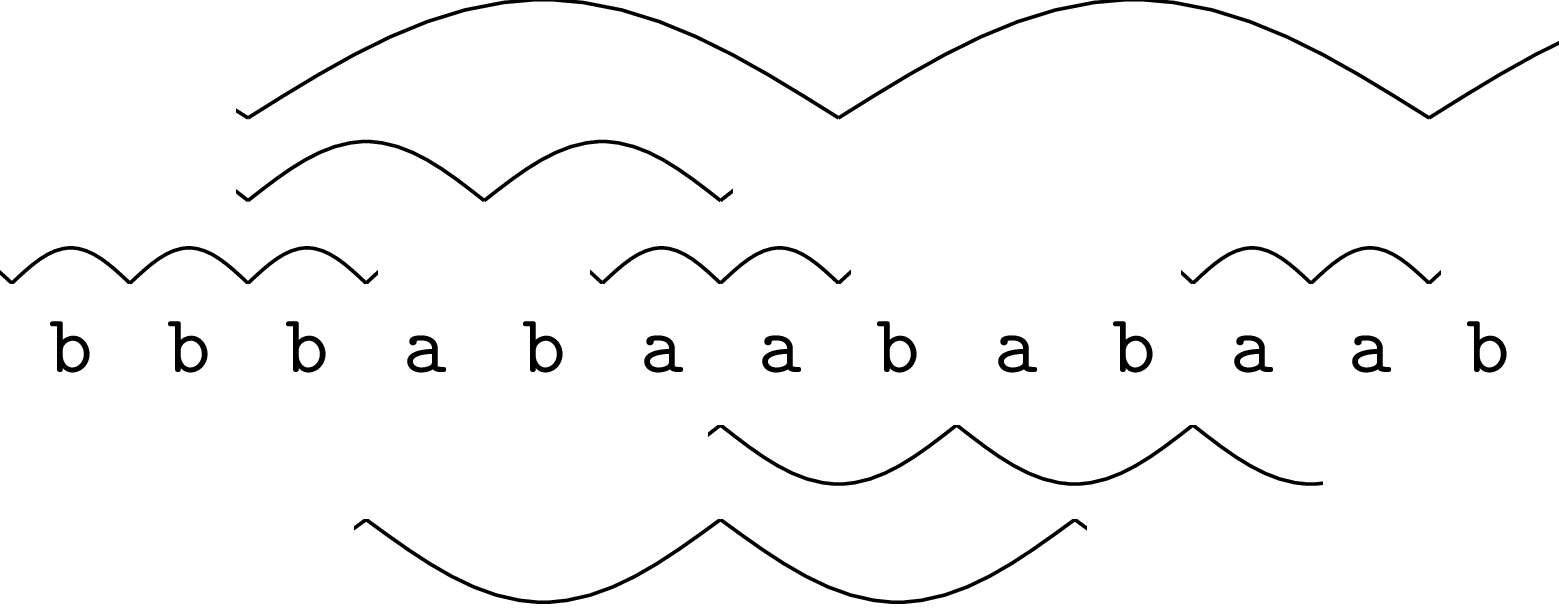
Słowo bbbabaababaab ma 7 maksymalnych okresowości. Każdy łuk oznacza jedno powtórzenie okresu w okresowości; niektóre powtórzenia są ucięte. Przykładowo na trzeciej pozycji słowa zaczynają się dwie maksymalne okresowości, baba o okresie 2 i babaababaab o okresie 5.

Po co rozważać maksymalne okresowości w słowie? Przede wszystkim reprezentują one każdy możliwy fragment okresowy słowa. Faktycznie, każdy fragment okresowy albo sam już jest maksymalną okresowością, albo można go maksymalnie rozszerzyć w obie strony aż do uzyskania maksymalnej okresowości. W szczególności wszystkie kwadraty (potęgi o wykładniku 2) w słowie, o których pisałem w numerze \(\Delta^{3}_{11}\), są reprezentowane przez maksymalne okresowości. Kluczową, a jednocześnie zupełnie nieoczywistą własnością maksymalnych okresowości jest to, że w słowie o długości \(n\) jest ich tylko \(O(n)\). To z kolei przekłada się na liczne zastosowania maksymalnych okresowości w algorytmach tekstowych, w co Czytelnik musi mi już uwierzyć…na słowo.

Dowód faktu, że liczba maksymalnych okresowości w słowie jest co najwyżej liniowa względem jego długości, został podany przez Romana Kolpakova i Gregory’ego Kucherova jeszcze w 1999 roku. Nie potrafili oni jednak podać żadnego ,,sensownego” współczynnika w tej zależności liniowej, choć na podstawie eksperymentów komputerowych wyszło im, że ten współczynnik powinien być równy po prostu 1. Przez kolejne lata różni badacze podawali dowody konkretnych oszacowań górnych z coraz to lepszymi stałymi, nierzadko posiłkując się obliczeniami komputerowymi. W szczególności pierwszą konkretną stałą w oszacowaniu, równą 5, uzyskał Wojciech Rytter w 2006 roku. W 2011 roku Maxime Crochemore wraz ze współpracownikami, wykorzystując cały klaster komputerów, uzyskał oszacowanie górne ze współczynnikiem \(\mbox{1,029}\). Wreszcie w 2017 roku zespół badaczy z Japonii, pod kierunkiem Hideo Bannai, udowodnił, że słowo długości \(n\) ma co najwyżej \(n\) maksymalnych okresowości. Udało im się to zrobić bez wykonywania jakichkolwiek obliczeń komputerowych, tylko właśnie za pomocą słów Lyndona.

Ostateczny dowód jest na tyle elementarny, że możemy go w tym miejscu naszkicować. Główny pomysł polega na tym, żeby każdej maksymalnej okresowości przypisać jedną pozycję w słowie, zwaną pozycją specjalną, tak aby różnym maksymalnym okresowościom przypisać różne pozycje specjalne. W ten sposób automatycznie otrzymamy żądane ograniczenie górne. Aby nie męczyć się z pewnymi szczegółami technicznymi, w tym artykule udowodnimy jedynie słabszą wersję tezy, że każda pozycja specjalna może być przypisana co najwyżej dwóm maksymalnym okresowościom; stąd wyniknie, że w słowie o długości \(n\) jest co najwyżej \(2n\) maksymalnych okresowości.

Przyjmiemy także, że rozpatrywane słowo \(s\) jest nad alfabetem binarnym \(\{\mathtt{a},\mathtt{b}\}\) (co trochę uprości argumentację).

Pozycje dowolnego słowa \(s\) będziemy numerowali od 1. Przez \(s[i]\) oznaczymy literę znajdującą się na \(i\)-tej pozycji słowa \(s\), a przez \(s[i..j]\) oznaczymy fragment \(s[i] \ldots s[j]\). Oprócz słów Lyndona, w konstrukcji używa się słów anty-Lyndona, które są (ściśle) największe w porządku leksykograficznym wśród swoich rotacji. Niech \(u=s[i..j]\) będzie maksymalną okresowością o okresie \(p\) w słowie \(s\), a \(x=s[j+1]\) będzie literą, która występuje w słowie \(s\) tuż za fragmentem \(u\). Wtedy pozycją specjalną maksymalnej okresowości \(u\) będzie taka pozycja \(k \in \{i,\ldots,i+p-1\}\), że:

1. jeśli \(x=\mathtt{a}\) lub \(x\) nie istnieje (bo \(j\) jest ostatnią pozycją w słowie), to \(s[k..(k+p-1)]\) jest słowem Lyndona,

   W przypadku alfabetu o dowolnej liczbie liter definicja pozycji specjalnej nieco się komplikuje – decyzję o wyborze przypadku (a) lub (b) podejmujemy, porównując litery \(s[j + 1]\) oraz \(s[j + 1 - p]\).

2. jeśli \(x=\mathtt{b}\), to \(s[k..(k+p-1)]\) jest słowem anty-Lyndona.

Przykład przypisania pozycji specjalnych można znaleźć na poniższym rysunku.

Pozycje specjalne maksymalnych okresowości oznaczono gwiazdkami.

Potrzeba chwili, żeby tę definicję przetrawić. Zacznijmy od uzasadnienia, że każda maksymalna okresowość ma pozycję specjalną. Jeśli maksymalna okresowość \(s[i..j]\) ma okres 1 (np. \(s[1..3]\) na rysunku), to nie mamy wyboru, i jej pozycją specjalną musi być pozycja \(k=i\). W ogólności zauważmy, że fragmenty długości \(p\) postaci \(s[k..(k+p-1)]\) dla \(k \in \{i,\ldots,i+p-1\}\) są kolejno wszystkimi rotacjami słowa \(s[i..(i+p-1)]\). Wynika to z faktu, że okres w maksymalnej okresowości musi się powtarzać co najmniej dwukrotnie. Żadne dwie takie rotacje, dla różnych \(k \in \{i,\ldots,i+p-1\}\), nie mogą być równe. Można zauważyć, że gdyby tak było, to słowo \(w\) o długości \(p\), takie że maksymalna okresowość \(u\) jest prefiksem potęgi \(w^m\), musiałoby być potęgą krótszego słowa. A zatem dokładnie jedna z tych rotacji będzie najmniejsza, a jedna największa w porządku leksykograficznym, i to one wyznaczą szukane słowo Lyndona i słowo anty-Lyndona.

Na przykład dla ,,górnej” maksymalnej okresowości \(s[3..13]\) na rysunku rozważane fragmenty długości \(p\) to kolejno babaa, abaab, baaba, aabab i ababa.

W formalnym uzasadnieniu tego spostrzeżenia może pomóc udowodniony w 1965 roku przez Finego i Wilfa lemat o okresowości: jeśli słowo \(s\) o długości \(n\) ma okresy \(p\) i \(q\) oraz \(p+q \le n+\text{nwd}(p,q)\), to \(s\) ma też okres \(\text{nwd}(p,q)\).

Wykażemy teraz, że jeśli pozycja \(k\) jest pozycją specjalną maksymalnej okresowości \(u=s[i..j]\) o okresie \(p\) wyznaczoną przez słowo Lyndona według przypadku [a], to \(s[k..(k+p-1)]\) jest najdłuższym słowem Lyndona zaczynającym się na pozycji \(k\). Załóżmy przez sprzeczność, że słowo \(s[k..r]\) dla pewnego \(r \ge k+p\) jest słowem Lyndona. Skorzystamy tu z równoważnej definicji słów Lyndona, według której muszą one być mniejsze leksykograficznie od wszystkich swoich właściwych sufiksów. Jeśli \(r \le j\), to słowo \(s[k..r]\) ma okres \(p\). Wtedy jednak sufiks \(s[(k+p)..r]\) byłby prefiksem \(s[k..r]\) (czyli w szczególności byłby od niego mniejszy), co przeczy równoważnej definicji słów Lyndona. Jeśli zaś \(r>j\), to sufiks \(s[(k+p)..r]\) zaczyna się od \(s[(k+p)..j]\mathtt{a}\), a słowo \(s[k..r]\) zaczyna się od \(s[k..(j-p)]\mathtt{b}\). Skąd ta litera b? Otóż gdyby tam była litera a, to maksymalną okresowość można by rozszerzyć o jedną pozycję w prawo, gdyż zachodziłoby \(s[j+1]=s[j+1-p]\). Mamy \(s[k..(j-p)]\mathtt{b}=s[(k+p)..j]\mathtt{b}\), czyli znów sufiks jest mniejszy. Otrzymana sprzeczność dowodzi, że rzeczywiście \(s[k..(k+p-1)]\) jest najdłuższym słowem Lyndona zaczynającym się na pozycji \(k\).

Na przykład dla maksymalnej okresowości \(s[3..6]\) z rysunku i \(k=4\) najdłuższym słowem Lyndona zaczynającym się na pozycji \(k=4\) w słowie \(s\) jest ab.

Dla rozważanego przykładu słowo \(s[4..6]=\mathtt{aba}\) nie jest słowem Lyndona, gdyż jego sufiks \(s[6..6]=\mathtt{a}\) jest od niego leksykograficznie mniejszy (bo jest jego prefiksem).

Przykładowo dla dowolnego \(r>j=6\) słowo \(s[4..r]=\mathtt{abaa}\ldots\) jest większe od słowa \(s[6..r]=\mathtt{aa}\ldots\)

Podobnie można wykazać, że w przypadku [b] fragment \(s[k..(k+p-1)]\) jest najdłuższym słowem anty-Lyndona zaczynającym się na pozycji \(k\). W tym celu wygodnie jest rozważyć porządek leksykograficzny, w którym b jest mniejsze od a; słowa anty-Lyndona są tak naprawdę słowami Lyndona w tym poniekąd odwróconym porządku leksykograficznym.

Oczywiście na każdej pozycji w słowie zaczyna się jedno najdłuższe słowo Lyndona i jedno najdłuższe słowo anty-Lyndona. Każde z tych słów możemy jednoznacznie rozszerzyć okresowo w lewo i w prawo, z okresem równym jego długości, otrzymując maksymalną okresowość, jeśli tylko okres powtórzy się w niej co najwyżej dwukrotnie. To ostatecznie dowodzi, że każda pozycja jest pozycją specjalną co najwyżej dwóch maksymalnych okresowości, i kończy nasz dowód.

Jedna pozycja może być pozycją specjalną dwóch maksymalnych okresowości. Okazuje się, że wtedy jedna z tych maksymalnych okresowości ma okres 1. Przykładowo ma to miejsce dla pozycji 6 na rysunku powyżej. Jeśli pozycję specjalną wybierzemy ze zbioru \(\{i+1,\ldots,i+p\}\) zamiast ze zbioru \(\{i,\ldots,i+p-1\}\), można udowodnić, że wtedy już każda pozycja słowa będzie pozycją specjalną co najwyżej jednej maksymalnej okresowości.

Na koniec warto zaznaczyć, że Bannai i in. w swojej pracy podali nowy, prostszy algorytm wyznaczania maksymalnych okresowości, a kluczową rolę w tym algorytmie pełni twierdzenie o jednoznacznym rozkładzie słowa na niemalejące słowa Lyndona. \[***\] Opowiemy teraz pokrótce o drugim nowym zastosowaniu słów Lyndona. Niech słowo \(s\) ma długość \(n\). Wyobraźmy sobie, że wszystkie sufiksy słowa \(s\) zostały uporządkowane rosnąco w kolejności leksykograficznej. Tablica sufiksowa słowa \(s\) zawiera pozycje początkowe sufiksów w tej właśnie kolejności. Jest ona zatem permutacją zbioru \(\{1,\ldots,n\}\).

Przykładowo, tablica sufiksowa słowa \(s=\mathtt{abaababa}\) to \(8,3,6,1,4,7,2,5\):

sufiks	pozycja początkowa
a	8
aababa	3
aba	6
abaababa	1
ababa	4
ba	7
baababa	2
baba	5

Tablica sufiksowa, obok drzewa sufiksowego, jest jedną z podstawowych struktur danych w algorytmach tekstowych. Na przykład jeśli mamy tablicę sufiksową słowa \(s\) o długości \(n\), to dla danego słowa-wzorca \(p\) o długości \(m\) możemy w czasie \(O(m \log n)\) znaleźć wszystkie jego wystąpienia w \(s\). W tym celu należy zauważyć, że zbiór sufiksów, na początku których występuje wzorzec \(p\), odpowiada spójnemu fragmentowi tablicy sufiksowej. Końce tego fragmentu możemy wyznaczyć za pomocą wyszukiwania binarnego.

Tablica sufiksowa została wprowadzona w 1990 roku przez Udiego Manbera i Gene’a Myersa. Korzystając z drzew sufiksowych, można ją skonstruować w czasie liniowym w przypadku słowa nad małym alfabetem. Jest też znany algorytm autorstwa Juhy Kärkkäinena i Petera Sandersa (2003 r.), który konstruuje ją w czasie liniowym bez użycia drzew sufiksowych. Tyle w teorii; natomiast praktyka pokazuje, że wszystkie te algorytmy są wolniejsze i bardziej pamięciochłonne niż algorytm o nazwie DivSufSort autorstwa Yuty Moriego działający w czasie \(O(n \log n)\). Co ciekawe, Yuta Mori przedstawił swój algorytm w postaci gotowego programu, z niewielką ilością komentarzy, opublikowanego w publicznym repozytorium.

Ten rozdźwięk między złożonością czasową a czasem działania na praktycznych danych był dość kłopotliwy dla badaczy zajmujących się algorytmami tekstowymi. Dopiero w 2021 roku Nico Bertram i in. w swojej pracy pt. Lyndon Words Accelerate Suffix Sorting przedstawili algorytm poparty poważną analizą teoretyczną i działający w praktyce szybciej niż DivSufSort. Jak tytuł pracy wskazuje, w ich algorytmie istotną rolę pełnią właśnie słowa Lyndona. Algorytm Bertrama i in. ma jednak wciąż ponadliniową złożoność czasową (choć korzysta z liniowej pamięci). Jego złożoność została poprawiona do liniowej, z jednoczesnym dodatkowym przyspieszeniem w praktyce, w pracy autorstwa Jannika Olbricha i in., opublikowanej bardzo niedawno, bo w 2022 roku.