* Uniwersytet Jana Kochanowskiego w Kielcach i Narodowe Centrum Badań Jądrowych w Warszawie
Redaktor Delty w latach 1991–1994.
W 1982 roku, wkrótce po ukończeniu studiów, zostałem wysłany do Zjednoczonego Instytutu Badań Jądrowych w Dubnej pod Moskwą, aby zajmować się zderzeniami jąder atomowych przy najwyższej wówczas dostępnej energii. Celem tego rozpoczynającego się właśnie programu badawczego było wytworzenie w laboratorium i poznanie własności egzotycznego stanu materii – plazmy kwarkowo-gluonowej, która występowała we wczesnym gorącym Wszechświecie, krótko po Wielkim Wybuchu.
Prawie 20 lat później cel został osiągnięty, a przynajmniej mocno się do niego zbliżyliśmy. W eksperymentach prowadzonych w Europejskim Centrum Badań Jądrowych w Genewie i Narodowym Laboratorium Brookhaven w stanie Nowy Jork zaobserwowano – prawda, że w dosyć pośredni sposób – krople plazmy kwarkowo-gluonowej, powstającej w zderzeniach najcięższych jąder atomowych rozpędzonych do energii wielokrotnie większej niż ta, która była dostępna w Dubnej.
Właśnie tam, w Rosji, na początku swej naukowej drogi przeczytałem niewielką popularnonaukową książeczkę „Szturm termojądrowej twierdzy” Gienadija Woronowa, opowiadającą o próbach – podejmowanych już wtedy od trzech dziesięcioleci – doprowadzenia do termojądrowej syntezy lekkich jąder atomowych, czyli odtworzenia w ziemskich warunkach procesu, dzięki któremu Słońce dostarcza nam życiodajne ciepło.
Gdy jądra atomowe lekkich pierwiastków, takich jak wodór, łączą się ze sobą, wydzielana jest energia. Aby do takiej syntezy doprowadzić, należy odpowiednio mocno podgrzać gaz tworzony przez atomy, powiedzmy, wodoru, tak aby elektrony oderwały się od jąder atomowych. Wówczas dochodzi do zderzeń jąder i staje się możliwa upragniona synteza. Materia w postaci jąder atomowych obdarzonych, jak pamiętamy, ładunkami dodatnimi i ujemnie naładowanych elektronów uwolnionych z atomów nazywana jest plazmą, dokładniej, plazmą elektromagnetyczną.
Ze wspomnianej książeczki dowiedziałem się, że plazma wykazuje zdumiewające własności, zupełnie odmienne od gazów, np. powietrza. Bardzo trudno ją kontrolować, uwięzić w pułapce. Plazma nie zachowuje się jak kulka umieszczona we wgłębieniu, która, jeśli ją potrącić, oscyluje wokół minimum, by po pewnym czasie wrócić do położenia na dnie wgłębienia. Plazma przypomina raczej kulę umieszczoną na szczycie wzniesienia. Wystarczy ją nieco wychylić z położenia chwiejnej równowagi, by potoczyła się w dół, szybko oddalając się od pierwotnego stanu. Fachowo mówimy, że plazma jest zwykle niestabilna – niewielkie zaburzenie jej stanu, fluktuacja nie zanikają z czasem, lecz gwałtownie narastają.
To jest właśnie główną przyczyną trudności w zbudowaniu termojądrowego reaktora. Historia kolejnych prób kontrolowania plazmy – licząca sobie teraz już nie trzy, a aż siedem dziesięcioleci – to historia odkrywania coraz to nowych rodzajów niestabilności – mechanizmów umożliwiających szybkie narastanie niewielkich zaburzeń.
Lektura owej niewielkiej książki miała istotny wpływ na moją naukową działalność. Skoro plazma elektromagnetyczna wykazuje bogactwo niestabilności, myślałem, to podobnie jest pewnie z plazmą kwarkowo-gluonową. Wszak tworzą ją kwarki i gluony – najmniejsze, najprostsze z poznanych dotychczas składników materii – oddziałujące wzajemnie dzięki ładunkom podobnym do ładunków elektrycznych zwanych kolorami. Te, tak jak kolory podstawowe, są trzech rodzajów i tak, jak kolory podstawowe łączą się w kolor biały, tak kwarki o trzech kolorach wzajemnie znoszą swoje ładunki i całość jest neutralna. Teoria opisująca siły występujące między kwarkami i gluonami nazywa się chromodynamiką i wykazuje istotne podobieństwa z elektrodynamiką, rządzącą zachowaniem ładunków elektrycznych.
Obserwacja, że plazma kwarkowo-gluonowa może być niestabilna podobnie jak plazma elektromagnetyczna, nie była szczególnie oryginalna. Nie ja jeden o tym pomyślałem. Pytanie było raczej inne: czy niestabilności mogą odgrywać istotną rolę w zachowaniu plazmy kwarkowo-gluonowej wytwarzanej w zderzeniach rozpędzonych jąder atomowych? A należy pamiętać, że plazma kwarkowo-gluonowa występuje w zupełnie innych warunkach niż elektromagnetyczna.
Właśnie wtedy, gdy zajmowało mnie pytanie o stabilność plazmy kwarkowo-gluonowej, zostałem redaktorem Delty, co wspominam jako świetną, trwającą kilka lat przygodę. Brałem aktywny udział w dyskusjach o kolejnych numerach pisma, redagowałem teksty wielu autorów, sam dużo pisałem. W dwóch artykułach, ,,Drgania plazmowe” i ,,Niestabilności plazmowe”, które ukazały się, odpowiednio, w \(\Delta^2_{93}\) i \(\Delta^9_{93}\), starałem się wyjaśnić w możliwie najprostszy sposób to, co mnie w owym czasie faktycznie pochłaniało.
W tym samym 1993 roku opublikowałem, jeśli nie najlepszy, to swój najczęściej cytowany artykuł naukowy, w którym dowodziłem, że pewna niestabilność, zwana filamentacyjną, może występować w plazmie kwarkowo-gluonowej powstałej w zderzeniu jąder. Ku memu rozczarowaniu rzecz nie wywołała żadnego zainteresowania, więc na jednej z konferencji złapałem znanego fizyka Larry’ego McLerrana i przymusiłem niejako do wysłuchania opowieści o tym, co udało mi się zrobić.
– Dlaczego ta niestabilność miałaby występować? – Larry zapytał, gdy skończyłem.
– Tak wychodzi z rachunków – mówię.
– To żadne tłumaczenie. Jeśli ten wynik ma sens, to powinieneś umieć go tak wyjaśnić, żeby zrozumiała moja żona.
Dodam, że Alice McLerran nie była fizykiem, lecz antropologiem i autorką książek dla dzieci.
Krytyka McLerrana była dotkliwie trafna. Praca w Delcie dostarczała licznych przykładów, że skomplikowane problemy dają się prosto wyjaśnić, jeśli je dobrze zrozumieć. Wspomniane teksty dokumentują moje własne wysiłki uchwycenia mechanizmów zjawisk plazmowych w najprostszych możliwych terminach. Jednak z przewidywaną niestabilnością filamentacyjną nie było łatwo. Po jakichś dwóch latach rozmyślań i studiowania literatury udało mi się w końcu rzecz zrozumieć, i opublikowałem w czasopiśmie naukowym elementarne objaśnienie. Z Deltą już się wtedy rozstałem i nie było okazji, aby przedstawić je na łamach tego pisma. Rocznicowy numer stwarza świetną okazję, by wrócić do problemu.
Wyobraźmy sobie tedy gaz cząstek naładowanych dodatnio i ujemnie. Niech to będą elektrony o ładunku ujemnym i ich antycząstki – pozytony o ładunku dodatnim. Dodam, że taka właśnie plazma występuje w różnych układach astrofizycznych, więc przykład nie jest czysto akademicki. Dalej przyjmijmy, że średnie liczby elektronów i pozytonów w każdym punkcie układu są sobie równe, więc plazma jest lokalnie elektrycznie neutralna. Nie występują też w niej prądy elektryczne, gdyż wraz z elektronami o danej prędkości mamy też w układzie pozytony ze zbliżonymi prędkościami.
Kluczową okolicznością umożliwiającą wystąpienie niestabilności jest anizotropowy charakter rozkładu prędkości elektronów i pozytonów. Anizotropowość oznacza, że prawdopodobieństwo znalezienia elektronu lub pozytonu z daną prędkością zależy od jej kierunku. Załóżmy zatem, że średnia prędkość cząstek naszego układu w kierunku osi \(z\) jest większa niż w kierunkach \(x\) i \(y\). Wyobraźmy sobie teraz, że na skutek fluktuacji kilka elektronów lub pozytonów poruszających się w kierunku osi \(z\) znalazło się obok siebie. Oznacza to, że w układzie pojawia się prąd elektryczny płynący w kierunku \(z\).
Zwróćmy uwagę, że wystąpienie takiego fluktuacyjnego prądu jest bardziej prawdopodobne w kierunku \(z\) niż w kierunkach \(x\) i \(y\). Dzieje się tak dlatego, że wielkość prądu jest proporcjonalna do unoszonego ładunku i jego prędkości. Średnia zaś prędkość wzdłuż osi \(z\) jest z założenia większa niż wzdłuż osi \(x\) lub \(y\).
Przyjęliśmy, że prądy w układzie, średnio rzecz biorąc, nie występują, co oznacza, że nadmiarowi elektronów w jednym miejscu będzie towarzyszył niedomiar w drugim. A zatem jeśli w danym miejscu pojawił się fluktuacyjny prąd w kierunku osi \(z\), to gdzieś obok wystąpi prąd płynący w przeciwnym kierunku.
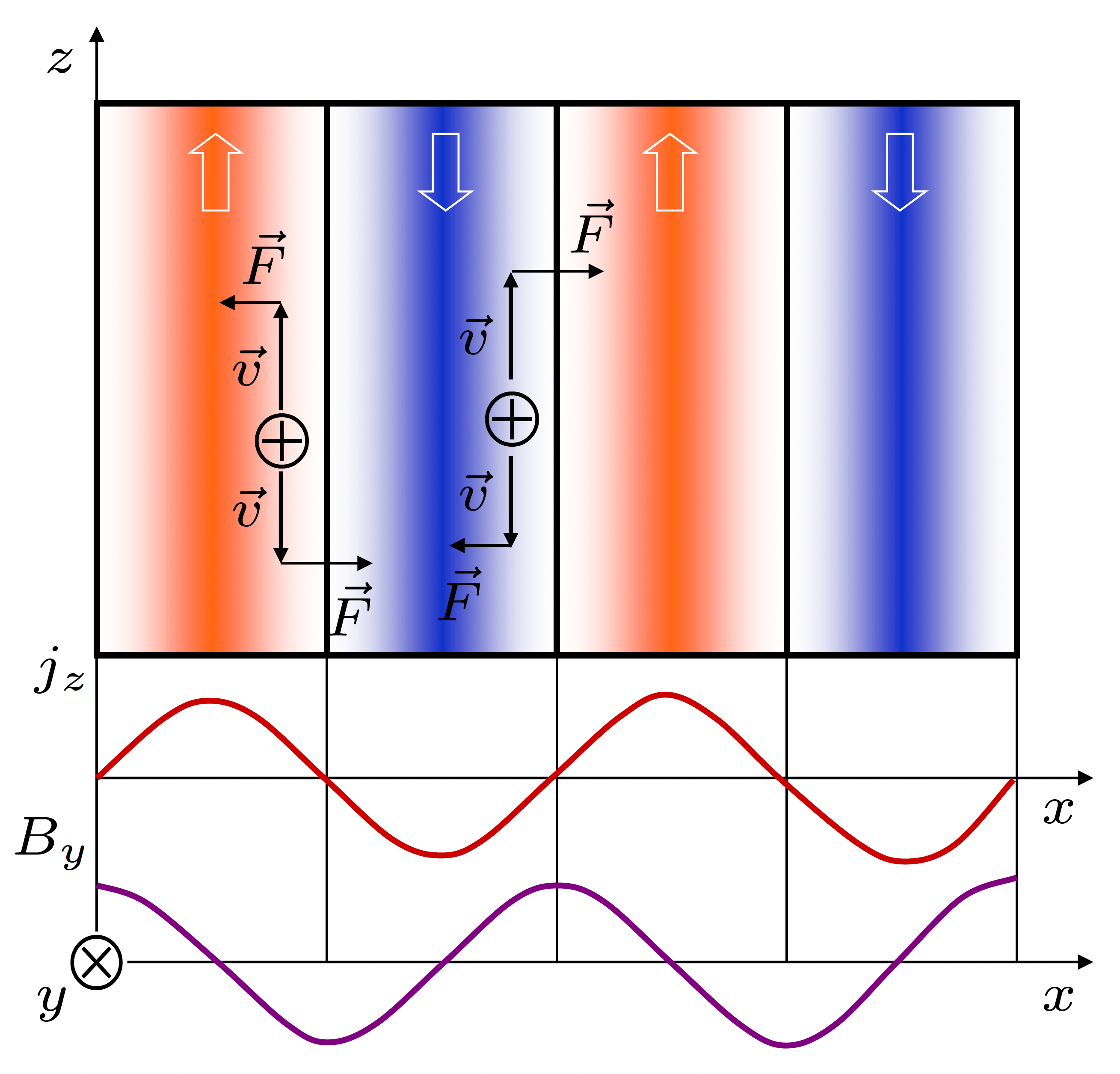
Tę pierwszą część opowieści możemy podsumować następująco. W neutralnym układzie elektronów i pozytonów, w którym cząstki mają prędkości w kierunku \(z\) średnio większe niż w kierunkach \(x\) i \(y\), występują znaczące fluktuacje prądu w kierunku \(z\). Innymi słowy, w układzie spontanicznie pojawiają się włókna z prądami płynącymi w przeciwne strony kierunku \(z\), pokazane na rysunku.
W drugiej, ,,dynamicznej”, części swojej opowieści postaram się wykazać, że fluktuacyjne prądy nie zanikają z upływem czasu, lecz przeciwnie – narastają.
Prądy elektryczne, jak wiemy, wytwarzają pole magnetyczne, a korzystając z prawa Ampère’a, nietrudno wykazać, że włókna prądowe pokazane na rysunku będą generowały pole magnetyczne w kierunku osi \(y\) o amplitudzie również tam uwidocznionej.
Jak wiemy, na cząstkę o ładunku \(q\) poruszającą się z prędkością \(\vec{v}\) w polu magnetycznym \(\vec{B}\) działa siła Lorentza \(\vec{F} = q \vec{v} \times \vec{B}\). Siła wywierana na dodatnio naładowany pozyton lecący równolegle do osi \(z\) pokazana jest na rysunku. Widzimy, że siła ta kieruje pozyton poruszający się zgodnie z kierunkiem prądu w danym włóknie ku centrum włókna. Natomiast pozyton poruszający się przeciwnie do kierunku prądu włókna stara się przerzucić do włókna sąsiedniego. Następuje więc spontaniczne sortowanie cząstek tak, że prąd w każdym włóknie rośnie i wytwarza coraz silniejsze pole magnetyczne, które z kolei coraz silniej wpływa na cząstki tworzące prąd. W ten sposób rozwija się niestabilność filamentacyjna.
W 2016 roku Larry McLerran otrzymał doktorat honoris causa Uniwersytetu Jagiellońskiego. Odbyła się piękna uroczystość w Collegium Maius, a potem gratulacje i rozmowy przy białym winie z uniwersyteckich winnic. Przypomniałem i podziękowałem honorowemu doktorowi za lekcję, jakiej mi przed laty udzielił. Dzięki przedstawionemu powyżej rozumowaniu, elementarnemu, choć wymagającemu uwagi przy jego śledzeniu, możliwość występowania filamentacyjnej niestabilności w plazmie kwarkowo-gluonowej została zaakceptowana i stała się elementem – prawda, że drobnym – fizyki zderzeń jądrowych przy najwyższych dostępnych energiach.