* Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Redaktor Delty w latach 1994–1999, od roku 2008 członek Komitetu Redakcyjnego.
9 kwietnia 1585 roku z portu w Plymouth wypłynęła flotylla, której trzon tworzyły: Tygrys, Czerwony Lew, Rogacz, Elżbieta i Dorota. Okręty pożeglowały w stronę dzisiejszej Wirginii. Organizatorem wyprawy był Sir Walter Raleigh, któremu rok wcześniej królowa Elżbieta I nadała przywilej kolonizowania i rządzenia ,,…wszelkimi odległymi, pogańskimi i barbarzyńskimi terytoriami, które nie są w posiadaniu chrześcijan ani nie są przez nich zamieszkane”, w zamian za jedną piątą złota i srebra, które można będzie tam wydobywać.
Niniejszy artykuł jest uwspółcześnioną i skróconą wersją rozdziału 6. z mojej książki Matematyka współczesna dla myślących laików [2].
Nie potrafię stwierdzić, na którym z okrętów płynął Thomas Harriot, astronom, etnograf, nawigator i matematyk – dwudziestopięcioletni asystent i zarazem protegowany Raleigha, absolwent St. Mary Hall w Oxfordzie z 1580 roku. Jednak kontakty Harriota z Raleighem, a później jego korespondencja z Johannesem Keplerem, leżą u źródeł sławnego problemu matematycznego o długiej, nieoczekiwanej historii.
Otóż Raleigh zlecił Harriotowi opracowanie optymalnego sposobu składowania kul armatnich na pokładzie. Harriot przygotował tabelę możliwych ułożeń, podając liczbę kul w stosie jako funkcję jego wysokości. Zaczął też badać wzory na sumę kwadratów kolejnych liczb naturalnych, a także rozważać, jaka jest struktura materii. Wiadomo o tym dzięki zachowanej korespondencji Harriota z Keplerem, z lat 1606–1607, w której obaj dyskutowali m.in., dlaczego promień świetlny, padając na powierzchnię przezroczystego ośrodka, zostaje częściowo odbity, a częściowo załamany. Teza Harriota (wyrażona współczesnym językiem) brzmiała: materia ma strukturę atomistyczną i dlatego gładkie na pozór powierzchnie nie są wcale jednorodne. Kepler z czasem przyjął ten pogląd.
W 1611 roku w książeczce Noworoczny podarek albo o sześciokątnych płatkach śniegu Kepler stwierdził, że symetrię śnieżynek powoduje ziarnista struktura materii, pisał o sposobach gęstego, ścisłego układania kul, a także wyraził przypuszczenie, nazwane później hipotezą Keplera, głoszące, że lepiej układać identycznych kul, niż Harriot proponował Raleighowi, nie można. Na dowód przyszło matematyce czekać blisko 400 lat…
Dostępne jest polskie wydanie Noworocznego podarku z 2006 roku (Wydawnictwa UW), z obszernym, bardzo ciekawym wstępem Zdzisława Pogody.
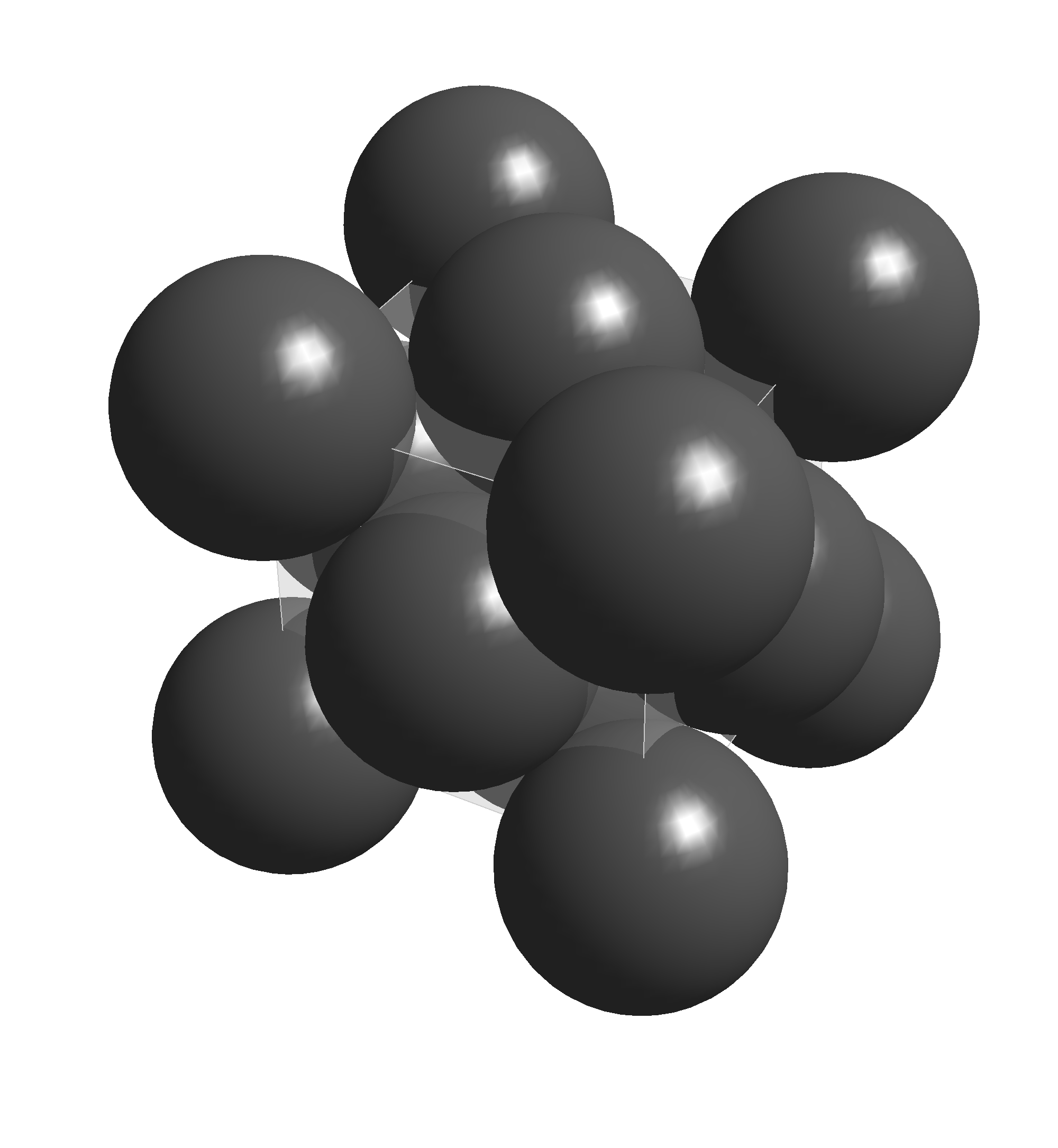
Spójrzmy na ułożenie identycznych kul w piramidę, nazywane upakowaniem
sześciennym, ściennie centrowanym (krótka nazwa to upakowanie
fcc, od angielskiego face centered cubic lattice).
Środki kul
jednej warstwy tworzą siatkę kwadratów; każda kula dotyka czterech innych. Kule
z kolejnej warstwy leżą w zagłębieniach między kulami poprzedniej. Gdy weźmiemy
\(5+4+5=14\) kul z trzech warstw – dwie piątki od góry i na spodzie, każda
ułożona w krzyż, oraz środkową czwórkę ułożoną w kwadrat, to środki ośmiu
z tych kul będą w wierzchołkach pewnego sześcianu, a środki pozostałych
sześciu – w środkach jego ścian (rys. 1).
Prowadząc cięcia wzdłuż ścian sześcianu, otrzymalibyśmy klocek, a w nim sześć
połówek kul i osiem fragmentów kul w wierzchołkach (rys. 2).
Takimi klockami można wypełniać całą przestrzeń. Hipoteza Keplera wyrażona potocznie brzmi: gęściej układać kul nie można; próba użycia nieregularnych ułożeń nic nie da.
Rys. 1
Rys. 2
Obliczmy gęstość upakowania fcc.
Przekątna sześcianu jest czterokrotnie dłuższa od promienia kuli równego 1. Krawędź takiego sześcianu to \(4/\sqrt{2}=2\sqrt{2}\), a jego objętość to \((2\sqrt{2})^3 = 16 \sqrt{2}\). Objętość kuli to \(\frac 43 \pi\), więc łączna objętość fragmentów kul zawartych w sześcianie wynosi
\[\biggl(8 \cdot \frac 18 + 6 \cdot \frac 12\biggr)\frac 43 \pi
= \frac{16 \pi }{3}\, .\]
Stosunek obu liczb to \(\pi/(3\sqrt{2})=\pi/\sqrt{18}\) i taka też jest
szukana gęstość.
W ogólności gęstość upakowania to granica górna stosunku objętości tych (części) kul danego upakowania, które są zawarte w kuli \(B(0,R)\), do objętości tej kuli, tzn. do \(4\pi R^3/3\), przy \(R\to +\infty\). Taka definicja działa również dla upakowań niesymetrycznych, gdzie w różnych obszarach przestrzeni kule są upakowane na przemian rzadziej i gęściej.
Upakowanie fcc można uzyskać, układając
kule (na pozór) inaczej.
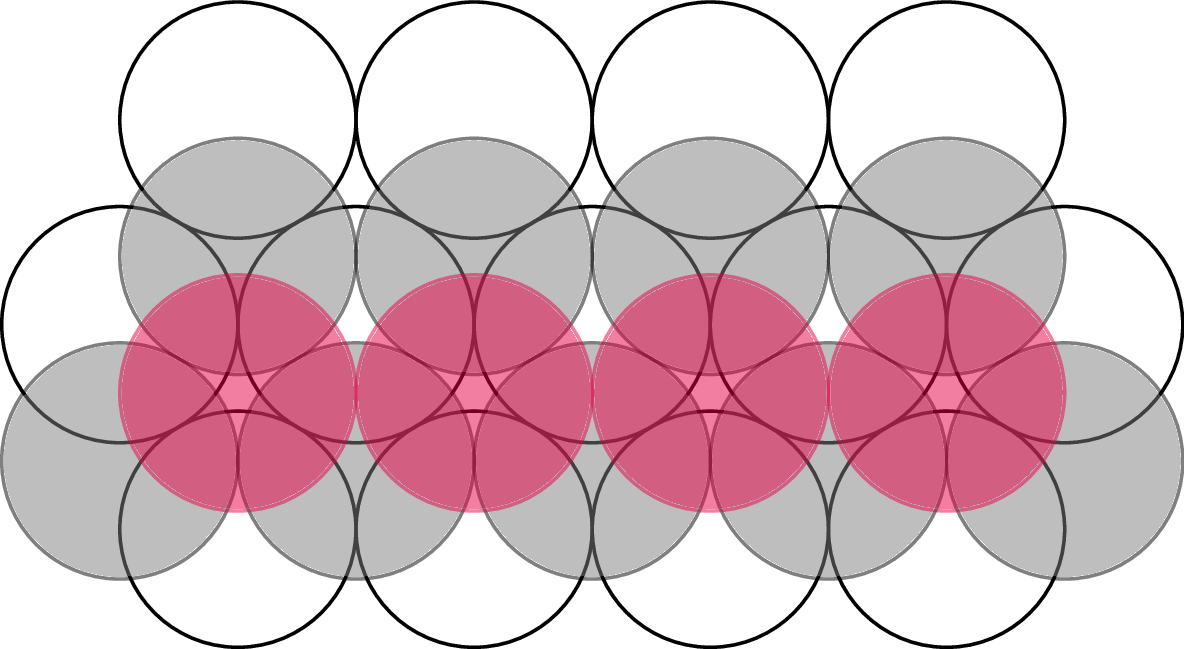
Weźmy płaską warstwę gęsto ściśniętych kul, których
środki są wierzchołkami siatki trójkątów równobocznych.
Z góry zobaczymy koła
wpisane w identyczne sześciokąty foremne wypełniające płaszczyznę. Zauważmy, że
każdą taką warstwę kul ułożonych nad jednakowymi sześciokątami foremnymi można
nałożyć na poprzednią na dwa różne sposoby. Nie da się wypełnić
wszystkich zagłębień naraz; można wypełnić tylko co drugie. Patrząc od góry,
możemy np. widzieć kolejne warstwy, powtarzające się w rytmie
\(a,b,c,a,b,c,\ldots\) lub w rytmie \(a,b,a,b,\ldots\) (rys. 3). Można sprawdzić, że rytm
walczyka, \(a,b,c,a,b,c,\ldots\) daje opisane wyżej upakowanie fcc.
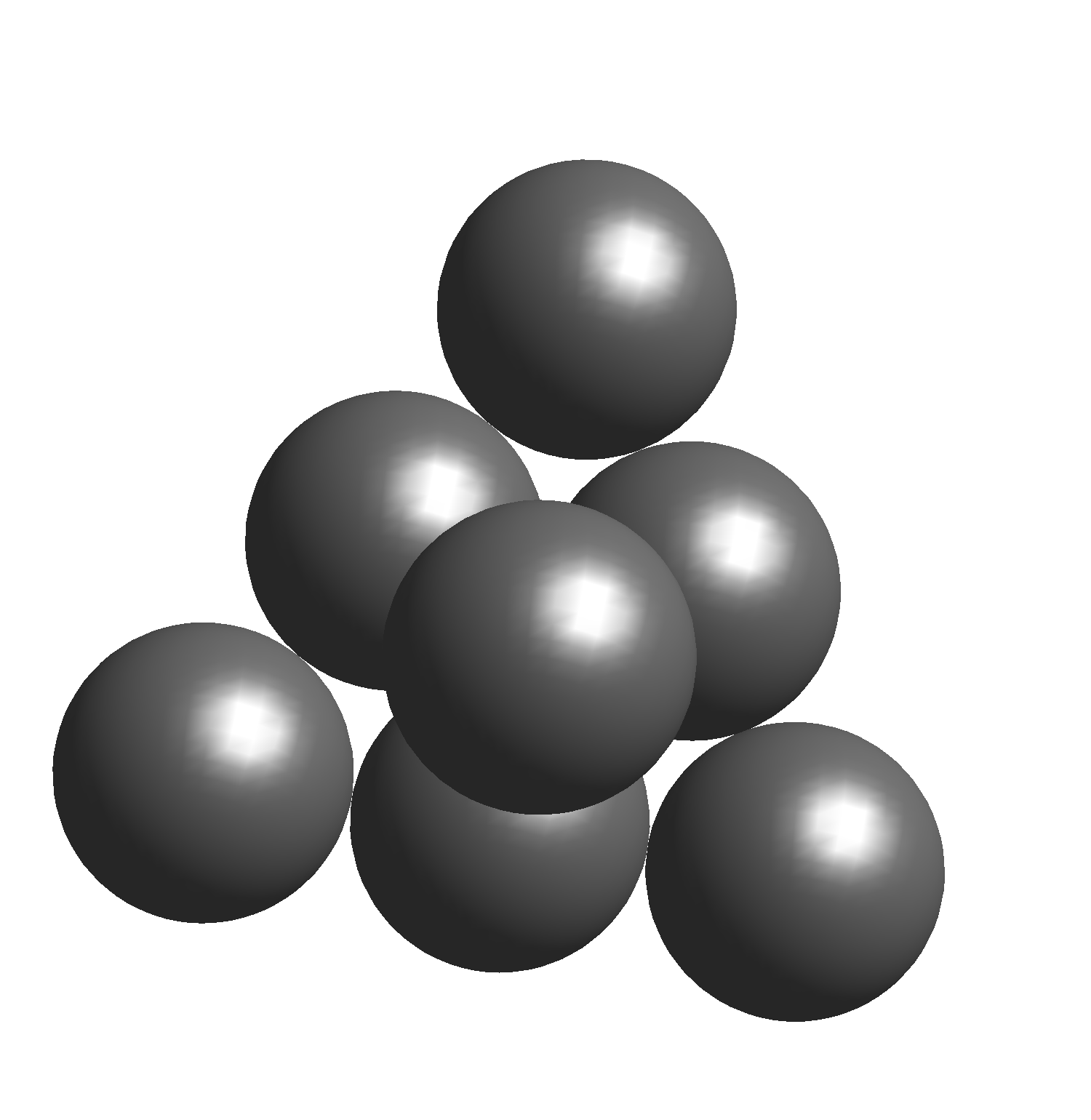
Wykonajmy w tym celu następujący eksperyment myślowy: wyobraźmy sobie
szóstkę tych kul, z jednej warstwy, ułożonych w trójkąt. Na wierzchu
tego trójkąta – symetrycznie, w środkowym zagłębieniu – połóżmy siódmą kulę (rys. 4).
Wyobraźmy sobie teraz, że cała siódemka została sklejona w sztywną konstrukcję.
Biorąc dwie kopie takiej konstrukcji i stykając je podstawami (wierzchołki
trójkątów powinny być skierowane w przeciwne strony, a kule jednej warstwy trzeba
wpasować we wgłębienia drugiej), uzyskamy 14 kul o środkach w wierzchołkach
i środkach ścian sześcianu. Obie siódemki kul uważny Czytelnik może wskazać na
rysunku na poprzedniej stronie.
Rys. 3. Białe kule należą do warstwy typu \(a\), szare do warstwy \(b\), zaś kolorowe do \(c\)
Rys. 4
Przy układzie warstw \(a,b,a,b,\ldots\) środki kul tworzą tzw. kratę
sześciokątną gęstą, a ułożenie nazywa się upakowaniem sześciokątnym
gęstym.
Gęstość tego upakowania jest równa
gęstości upakowania fcc.
Co więcej, każdy nieskończony (,,w obie strony”) ciąg liter \(a,b,c\), w którym każde dwie sąsiednie litery są różne, odpowiada innemu układowi kolejnych warstw kul. Różnych ułożeń o tej samej gęstości jest więc continuum, a wśród nich – cała masa nieokresowych, bez powtarzalnej symetrii!
Przy dodatkowym wymaganiu, by środki kul tworzyły regularną kratę, hipoteza Keplera staje się łatwiejsza. W takiej wersji udowodnił ją Carl Gauss w 1831 roku. Jego dowód opiera się na tym, że założenie symetrii upakowania pozwala przechodzić od lokalnych wniosków o ułożeniu kul do wniosków globalnych: w optymalnym upakowaniu jakieś dwie kule muszą się dotykać (inaczej moglibyśmy nieco zwiększyć wszystkie kule, tzn. gęstość upakowania); później można wnioskować, że istnieją całe rzędy i warstwy dotykających się wzajemnie kul.
W uproszczonej, płaskiej wersji problemu odpowiednik hipotezy Keplera udowodnił w 1890 roku norweski matematyk Axel Thue. Jego dowód jest elementarny; patrz np. przeglądowy artykuł Halesa [1], a także rozdział 6 w [2]. Dziesięć lat po dowodzie Thuego, w roku 1900, David Hilbert umieścił hipotezę Keplera na swej słynnej liście problemów (jako część problemu XVIII).
Zanim wspomnę o samym dowodzie hipotezy Keplera, chcę napisać, co stanowi o jej trudności. Pierwszy powód jest banalny: geometria przestrzenna jest trudniejsza od płaskiej. Powód drugi to brak symetrii; wydaje się, że ten brak może tylko zmniejszyć gęstość upakowania, ale to jeszcze nie dowód, prawda? Każdy, kto dopychał walizkę kolanem, wie, że sukces wiąże się z zaburzeniem symetrii starannie ułożonych ubrań.
Najważniejszy jest trzeci powód. Otóż w płaskiej wersji hipotezy Keplera, rozwiązanej przez Thuego, jest tak, że to, co optymalne lokalnie, można po prostu zrealizować globalnie. W przestrzeni już tak nie jest; żeby to wyjaśnić, wytłumaczmy najpierw, co to są komórki Woronoja. Otóż komórka Woronoja danej kuli w upakowaniu to zbiór tych punktów przestrzeni, które są bliżej środka tej kuli niż środków innych kul z upakowania. Zbiór punktów równoodległych od ustalonych punktów \(A,B\) w przestrzeni to płaszczyzna; dlatego komórki Woronoja każdego upakowania kul są wielościanami wypukłymi.
Gieorgij Fieodosjewicz Woronoj żył w latach 1868–1908; od 1894 roku wykładał na Uniwersytecie Warszawskim. Był promotorem Wacława Sierpińskiego i wg. danych Mathematics Genealogy Project ma ponad 4 tys. ,,potomków” (osób, które łączy z nim skończona liczba więzów doktorant–promotor). Jedna czwarta z nich to potomkowie Antoniego Zygmunda, który po wojnie pracował na Uniwersytecie w Chicago.
Jeśli upakowanie ma mieć dużą gęstość, to jego komórki Woronoja powinny być małe. Jak jest na płaszczyźnie dla upakowań kół o promieniu 1? Tam komórki Woronoja to wielokąty wypukłe. Okazuje się, że komórką Woronoja o najmniejszym możliwym polu jest sześciokąt foremny opisany na kole. Taką komórką można parkietować płaszczyznę i na tym opiera się dowód Thuego; gęstość optymalnego upakowania kół jest taka sama jak najlepszy stopień wypełnienia pojedynczej komórki.
W przestrzeni jest inaczej.
Okazuje się mianowicie, że kula wpisana w dwunastościan foremny zajmuje nieco
ponad 0,754 jego objętości, a to więcej niż \(\pi
/\sqrt{18}=0{,}74048\ldots\) (Dwunastościan foremny to komórka Woronoja, którą
jedna kula wypełnia najbardziej jak się da, ale to osobna opowieść).
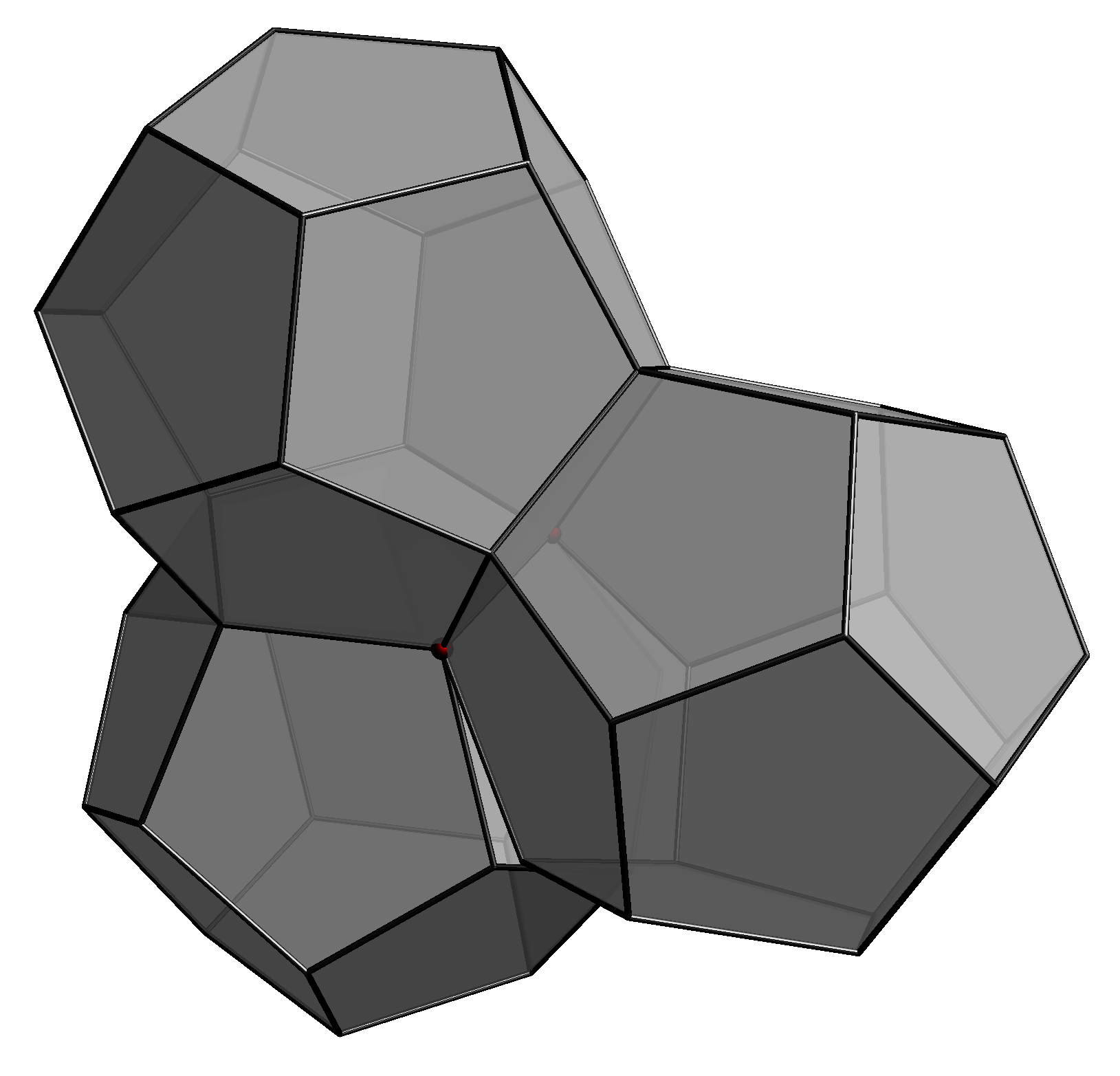
Kłopot w tym, że dwunastościanami foremnymi nie da się wypełniać
przestrzeni (rys. 5).
Niemniej zasadne jest pytanie: a może jeśli w jakimś upakowaniu
wciśniemy, kosztem lekkiego luzu tu i ówdzie, dużo miejsc, gdzie komórki
Woronoja kul będą dwunastościanami foremnymi, to okaże się, że globalnie
zyskamy przewagę nad upakowaniem fcc? Cała trudność polega na tym, żeby
wykluczyć wszystkie takie sytuacje, godząc się jednak z tym, że upakowanie może
być pozbawione symetrii.
Rys. 5
W 1953 roku węgierski matematyk Fejes Tóth wskazał w istocie pewną drogę do dowodu hipotezy Keplera – udowodnił mianowicie, że wynika ona z pewnego układu ważonych nierówności, jakie mają spełniać objętości komórek Woronoja danego upakowania. Przez kolejnych 40 lat z hipotezą Keplera nie stało się nic; w 1976 roku John Milnor pisał, że to skandal, że wciąż jest nieudowodniona.
W latach 1993–1998 Thomas Hales, wspomagany w części prac przez doktoranta Samuela Fergusona, przeprowadził dowód hipotezy Keplera, doskonaląc sugestię Tótha. Esencja pomysłu jest następująca: zamiast minimalizować objętości komórek Woronoja, trzeba minimalizować nieco inną funkcję, dodając do objętości każdej komórki poprawkę – taką aby suma poprawek dla wszystkich kul zawartych w wielkiej kuli \(B(0,R)\) była znikoma w porównaniu z \(R^3\). Sedno dowodu to konstrukcja takich poprawek. Margines swobody konstrukcji jest spory, ale liczba niezbędnych obliczeń ogromna.
Cały dowód Halesa zajmuje kilka prac o łącznej długości mniej więcej 250 stron. Do tego dochodzą obliczenia wykonywane za pomocą komputera; ich dokumentacja zajmuje kilka gigabajtów danych. Metody użyte w dowodzie obejmują, prócz geometrii i topologii, teorię optymalizacji (liniowej i nieliniowej), teorię grafów i kombinatorykę.
W 2005 roku 120-stronicowa praca Halesa omawiająca bardzo szczegółowo ramy dowodu i jego strategię została opublikowana w Annals of Mathematics, które wielu matematyków uznaje za najbardziej prestiżowe na całym świecie czasopismo w naszej branży. Sprawdzał ją przez kilka lat dwunastoosobowy zespół recenzentów, który nie znalazł żadnych błędów, ale oczywiście nie mógł potwierdzić poprawności wszystkich użytych programów komputerowych. Redakcja Annals umieściła na okładce tomu odpowiednie zastrzeżenie. Uważam, że fakt ostatecznej publikacji pracy Halesa akurat w Annals, nie w czasopiśmie mniejszej rangi, należy uznać za znak czasu: dowody wspierane komputerowo są w matematyce akceptowane i akceptowalne. (Jest więcej takich znaków, nie tylko historie hipotezy Keplera i zagadnienia czterech barw).
W 2003 roku Hales rozpoczął realizację długofalowego projektu FPK; akronim pochodzi od angielskiego Formal Proof of Kepler. Celem było napisanie takiego dowodu hipotezy Keplera, który mógłby zostać czysto formalnie sprawdzony z pomocą któregoś z komputerowych systemów wspomagania dowodzenia. (Przykładem takiego systemu jest polski Mizar; inne to Coq, Isabelle czy HOL Light; w systemie Coq podano w 2004 roku sformalizowany dowód zagadnienia czterech barw. Takich narzędzi używa się skądinąd nie tylko do formalnej analizy rozumowań, ale i do badania poprawności programów komputerowych stosowanych np. w przemyśle, energetyce, lotnictwie, organizacji ruchu kolejowego). Sukces FPK anonsowano latem 2014 roku; praca Halesa i dwudziestu kilku współautorów (jest wśród nich polski informatyk Cezary Kaliszyk) ukazała się w 2017 roku w Forum Mathematicum.
Czy to koniec historii? Nie. Po pierwsze jest otwarte i bardzo ważne dziś pytanie, czy i jak możliwości dowodów wspieranych komputerowo zmienią – może za sprawą osiągnięć sztucznej inteligencji? – całą matematykę. Nie pokuszę się o odpowiedź. Po drugie bardzo naturalne dla matematyka jest inne pytanie: skoro wiadomo, jakie są optymalne, najgęstsze upakowania kul w wymiarach 2 i 3, to co się dzieje dla \(n>3\)? Dla wymiarów \(n\not=1,2,3,8,24\) optymalnych upakowań nie znamy. Natomiast w \(\mathbb R^8\) gęstość optymalnego upakowania kul wynosi \(\pi^4/384\) (a więc około 0,25), a w \(\mathbb R^{24}\) jest równa \(\pi^{12}/12!\). Dowody są klasyczne, bez wsparcia komputerowego. Za autorstwo pierwszego z tych wyników i udział w drugim Maryna Wiazowska 5 lipca 2022 roku w Helsinkach odebrała medal Fieldsa. Laudację o wynikach Wiazowskiej wygłosił jej współautor, Henry Cohn z MIT i Microsoft Research; druga afiliacja wiąże się z tym, że upakowania kul w wysokich wymiarach mają związek z konstrukcją tzw. kodów korekcji błędów, ale to znów temat na inną opowieść.
Bibliografia:
- Thomas Hales. Cannonballs and honeycombs. Notices Amer. Math. Soc. 47, no. 4 (2000).
- Paweł Strzelecki. Matematyka współczesna dla myślących laików. Wydawnictwa Uniwersytetu Warszawskiego, Warszawa 2011.