* Wydział Matematyki, Informatyki i Mechaniki, Uniwersytet Warszawski
Redaktor Delty w latach 2014–2022.
Czy wszystko da się wygooglować? Albo przynajmniej – czy będzie się dało za parę lat, gdy sztuczna inteligencja będzie zdecydowanie bardziej rozwinięta niż ostatni czat GPT-4? Niestety, okazuje się, że wobec niektórych pytań nawet wyszukiwarka Google okazuje się całkowicie bezradna. Doświadczyłem tego ostatnio, chcąc się dowiedzieć, jakiego koloru nie pokażą nam ekrany komputerów. Bo okazuje się, że ekrany nie wyświetlają wszystkich barw, które możemy zobaczyć ludzkim okiem, a tylko niektóre. I to nie dlatego, że są źle robione, ale z pewnych głębszych, bardzo interesujących przyczyn. Ale zacznijmy opowieść od początku.
Jak zapewne większość Czytelników wie, barwy na ekranie komputerów, telewizorów, komórek i innych urządzeń wyświetlane są w systemie RGB (od ang. Red, Green, Blue, czyli kolorów czerwonego, zielonego i niebieskiego). Każdy piksel na ekranie ma dla każdej z trzech barw podaną intensywność w skali od 0 do 255. Przykładowo trójka intensywności RGB \((255, 0, 0)\) to kolor czerwony, \((0, 0, 255)\) to niebieski, \((255, 255, 0)\) to żółty, \((0, 0, 0)\) to czarny, a \((0, 0, 100)\) to ciemnoniebieski. Przyzwyczailiśmy się do myślenia, że każdy kolor można reprezentować za pomocą trzech składowych: czerwonej, zielonej i niebieskiej, ale warto zadać sobie pytanie, skąd się to bierze. Przecież światło widzialne składa się z fal o różnych częstotliwościach i na przykład fala o długości 580 nm, którą ludzkie oko odbiera jako kolor żółty, nie jest w żadnym sensie sumą fal o częstotliwościach 650 nm (czerwony dla ludzkiego oka) i 550 nm (zielony dla ludzkiego oka). A jednak kolor żółty reprezentujemy jako trójkę \((255, 255, 0)\), czyli jako sumę kolorów zielonego i czerwonego. Dlaczego?
Zapewne doświadczeni Czytelnicy wiedzą lub domyślają się, że rozwiązanie zagadki tkwi w tym, jak nasze oczy odbierają kolory. Mianowicie: w ludzkim oku, na siatkówce, znajdują się światłoczułe komórki zwane czopkami. Większość ludzi ma trzy rodzaje czopków, wrażliwych na nieco różne długości fali. Czopki D (od: długofalowe) są najbardziej wrażliwe na światło czerwone, czopki Ś (średniofalowe) są najbardziej wrażliwe na światło zielone, a czopki K (krótkofalowe) są najbardziej wrażliwe na światło niebieskie. Nasz odbiór barwy światła zależy od tego, jak mocno pobudzone są czopki różnych rodzajów, i tylko w ten sposób jesteśmy w stanie odróżniać jedne kolory od drugich. A więc rozważane przez nas dla przykładu światło barwy żółtej pobudza mocno czopki typów D i Ś (czerwone i zielone), a mniej czopki typu K (niebieskie). Wyświetlany przez monitor kolor \((255, 255, 0)\) również pobudza mocno czopki D i Ś, a słabo czopki K. Dlatego nasze oko widzi ten kolor jako żółty, mimo że nie ma on nic wspólnego z monochromatycznym światłem żółtym.
Starsi Czytelnicy mogli przeczytać o tym 48 lat temu w artykule Jana Gaja Oko i barwa \(\Delta^{1}_{76}\).
Jako ciekawostkę dodajmy, że jedną z przyczyn daltonizmu może być brak jednego z typów czopków. Z drugiej strony niektóre kobiety mają cztery rodzaje czopków i w związku z tym dostrzegają więcej barw. Taką cechę, czy też umiejętność, nazywa się tetrachromatyzmem.
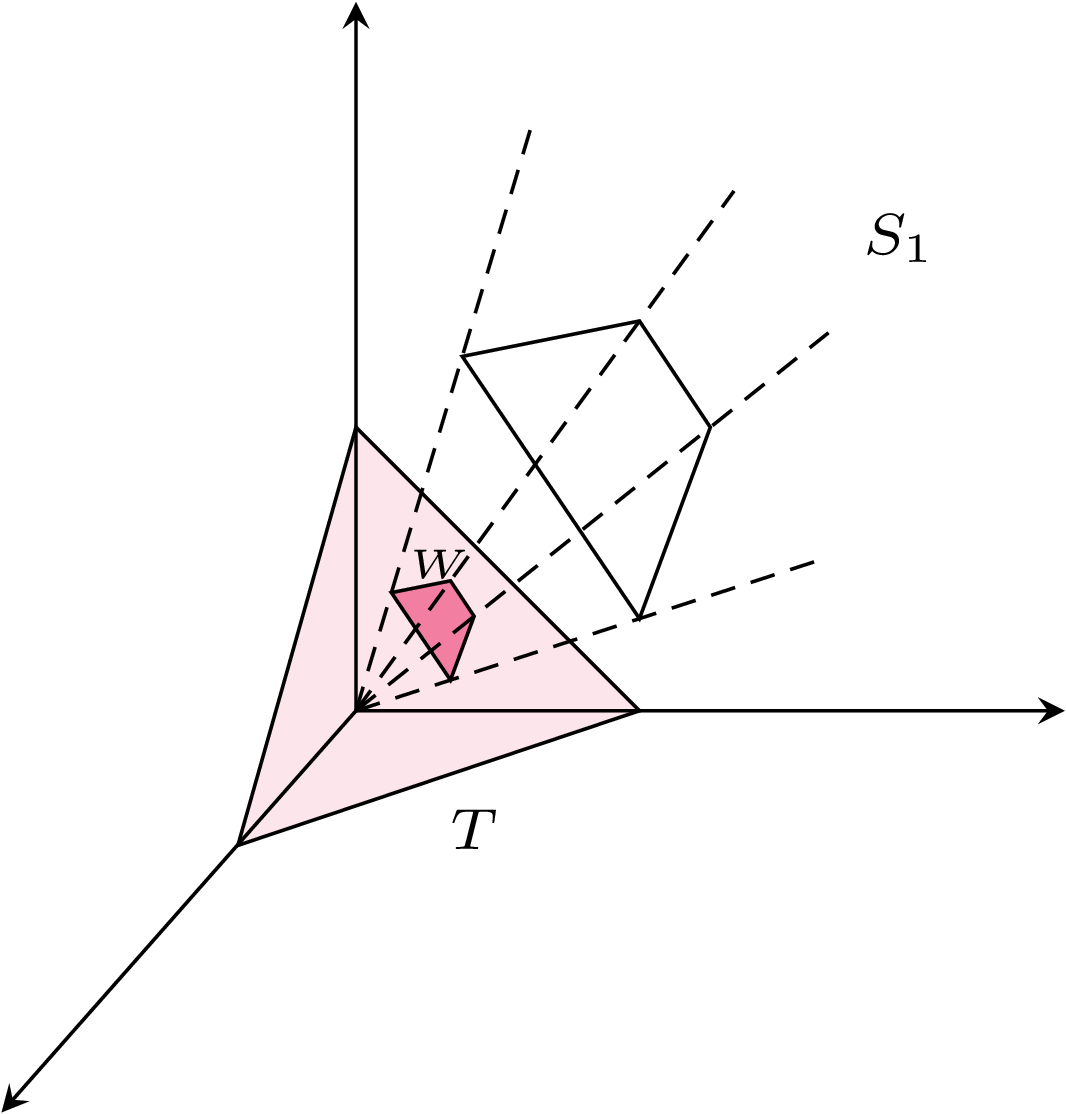
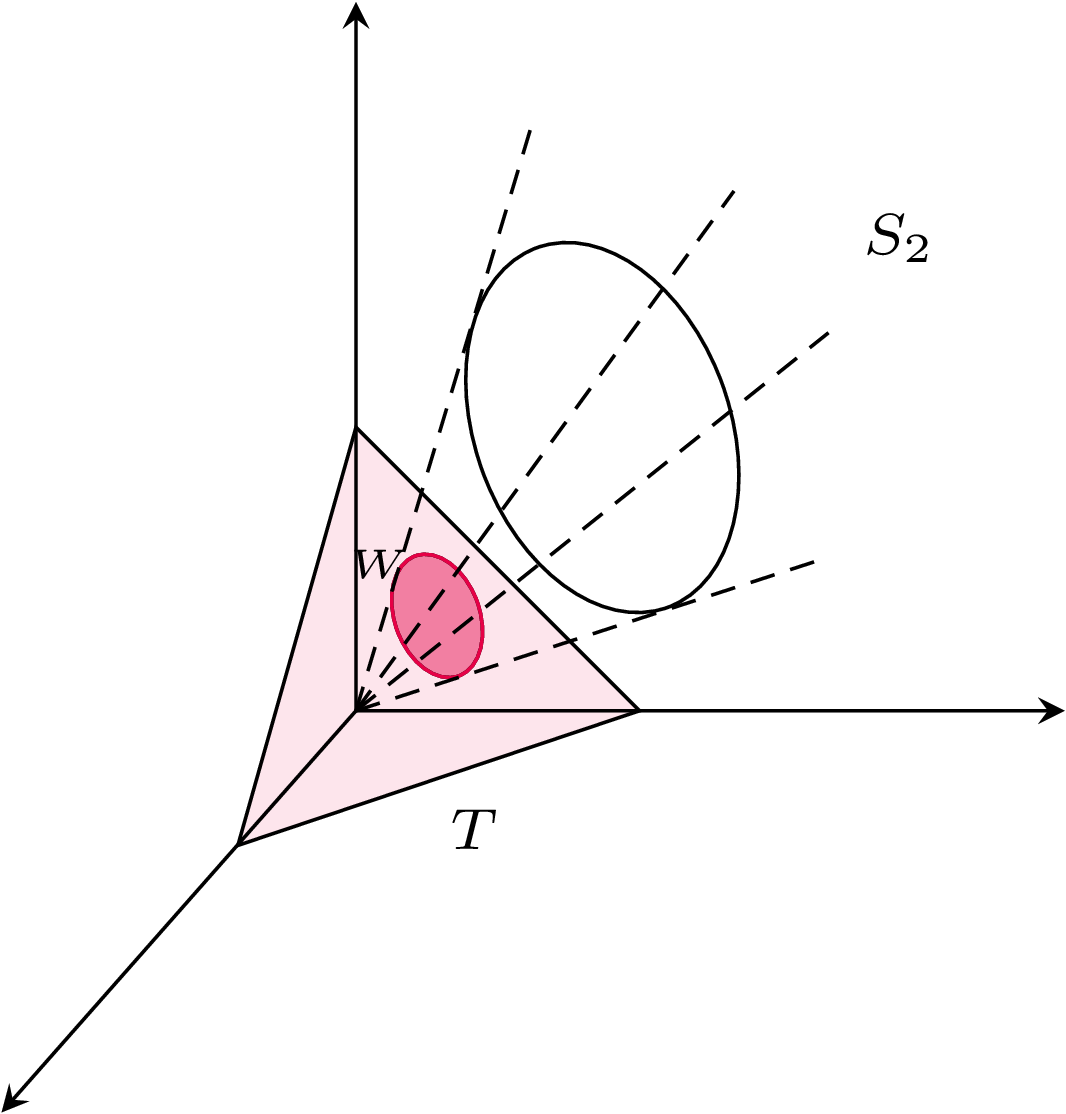
Po tym wstępie wróćmy jednak do początkowego pytania: czy monitory oparte na systemie RGB wyświetlają wszystkie kolory widoczne dla ludzkiego oka? A raczej poprawniej byłoby zapytać: czy te monitory są w stanie zasymulować dowolną możliwą reakcję czopków naszego oka na padające światło? Odpowiedź, jak już powiedzieliśmy na wstępie, brzmi: nie. Co więcej, każdy monitor działający na podobnej zasadzie, to znaczy wyświetlający trzy lub dowolną inną liczbę podstawowych kolorów, będzie mieć tę samą wadę. Żeby zrozumieć przyczynę tego zjawiska, przyjrzyjmy się dokładniej reakcjom naszego oka. Każde światło jakoś pobudza trzy typy naszych czopków – powiedzmy, że światło o widmie \(s\) powoduje sygnał od czopków czerwonych (D) w nasileniu \(R_s\), od czopków zielonych (Ś) w nasileniu \(G_s\), a od czopków niebieskich (K) w nasileniu \(B_s\). A więc całość reakcji na światło \(s\) to trójwymiarowy wektor \((R_s, G_s, B_s)\). Warto zadać pytanie: jak wygląda zbiór wszystkich możliwych do uzyskania wektorów – reakcji na światło. Oznaczmy go przez \(S_r\) (stożek reakcji), a zatem \(S_r = \{(R_s, G_s, B_s): s\) jest falą elektromagnetyczną\(\} \subseteq \mathbb R_{\geq 0}^3\). Przypomnijmy, że czopki D, Ś i K reagują nie tylko na światło czerwone, zielone i niebieskie, ale na wiele różnych częstotliwości światła, tylko w różnym natężeniu. Czyli na przykład światło niebieskie pobudza wszystkie czopki, tyle że najbardziej niebieskie, a czerwone i zielone mniej. Dlatego zbiór \(S_r\) okazuje się mieć ciekawe geometryczne własności i nie jest po prostu zbiorem wszystkich możliwych wektorów o nieujemnych wartościach \(\mathbb R_{\geq 0}^3\). Zauważmy najpierw, że zbiór \(S_r\) spełnia dwie własności: (1) jeśli \(v \in S_r\), \(\lambda \in \mathbb R_+\), to również \(\lambda v \in S_r\), oraz (2) jeśli \(v_1, v_2 \in S_r\), to również \(v_1 + v_2 \in S_r\). Istotnie, jeśli wektor \(v\) jest reakcją na jakieś światło \(s\), to wektor \(\lambda v\) będzie reakcją na światło \(\lambda s\), czyli światło o tym samym spektrum, tylko \(\lambda\) razy mocniejsze. Natomiast jeśli \(v_1\) jest reakcją na światło \(s_1\), a \(v_2\) jest reakcją na światło \(s_2\), to \(v_1 + v_2\) będzie reakcją na światło \(s_1\) świecące razem ze światłem \(s_2\), czyli na światło \(s_1 + s_2\). To oznacza, że zbiór \(S_r\) istotnie spełnia warunki (1) i (2) sformułowane powyżej, zbiory takie nazywamy stożkami. Żeby sobie wyobrazić, jak taki stożek może wyglądać, przyjrzyjmy się zbiorowi \(T = \{(x, y, z) \in \mathbb{R}^3_{\ge 0}: x + y + z = 1\}\), czyli trójkątowi rozpiętemu pomiędzy punktami \((1, 0, 0)\), \((0, 1, 0)\) oraz \((0, 0, 1)\). Każdy stożek \(S\) ma tę własność, że jego przecięcie z trójkątem \(T\) jest zbiorem wypukłym, bo jeśli \(u, v \in S\), to również \(\alpha u + (1-\alpha) v \in S\) dla dowolnego \(\alpha \in [0,1]\). Co więcej, każdy zbiór wypukły \(W\) zawarty w trójkącie \(T\) jednoznacznie wyznacza stożek: ten stożek to po prostu wektory ze zbioru \(W\) pomnożone przez jakąś liczbę \(\lambda \in \mathbb R_+\). A zatem żeby wyobrażać sobie stożki, wystarczy patrzeć na ich przecięcia z trójkątem \(T\). Na rysunkach 1 i 2 przedstawione są dwa przykłady stożków: \(S_1\) i \(S_2\).
Rys. 1
Rys. 2
Stożki \(S_1\) i \(S_2\) różnią się od siebie fundamentalnie. Przecięcie stożka \(S_1\) i trójkąta \(T\) to czworokąt: jego wierzchołkami są wektory \(v_1, v_2, v_3, v_4\). Natomiast przecięcie stożka \(S_2\) i trójkąta \(T\) to koło. Zauważmy, że każdy punkt stożka \(S_1\) może być wygenerowany z wektorów \(v_1, v_2, v_3, v_4\) poprzez aplikację reguł (1) oraz (2). Istotnie, możemy w ten sposób łatwo przedstawić każdy punkt we wnętrzu czworokąta \(S_1 \cap T\) jako średnią ważoną wektorów \(v_1, \ldots, v_4\), a potem ten wektor dowolnie wydłużyć lub skrócić. W takiej sytuacji mówimy, że stożek \(S_1\) jest skończenie generowany, bo da się go wygenerować za pomocą reguł (1) i (2) ze skończonej liczby wektorów. Można łatwo zauważyć, że stożek \(S\) jest skończenie generowany wtedy i tylko wtedy, gdy jego przecięcie z trójkątem \(T\) jest po prostu wielokątem. Wtedy jest on generowany przez wierzchołki tego wielokąta. Z drugiej strony, jeśli skończona liczba wektorów \(v_1, \ldots, v_n\) generuje stożek \(S\), to powstaje on jako otoczka wypukła punktów \(v_1, \ldots, v_n\), która następnie zostaje przeskalowana (możemy skracać lub wydłużać wektory, używając reguły (1)). Czyli stożek \(S_2\) nie jest skończenie generowany, bo jego przecięcie z trójkątem \(T\) to koło, a nie wielokąt. Intuicyjnie jest to jasne: żeby go wygenerować musielibyśmy użyć wszystkich wektorów na brzegu koła \(S_2 \cap T\), a tych jest nieskończenie wiele.
Jaki ma to związek z wyświetlaniem barw przez monitor? Otóż okazuje się, że zbiór \(S_r\) wszystkich możliwych reakcji oka ludzkiego na światło jest nieco zaokrąglony, a zatem nie jest skończenie generowany. Jaki z tego wniosek? Ano taki, że nie możemy go wygenerować ze skończenie wielu możliwych reakcji przez dodawanie i mnożenie. A przecież to dokładnie próbuje zrobić monitor. Światło \(r = (255, 0, 0)\) to kolor czerwony, wywołuje on jakiś wektor reakcji \(v_r = (R_r, G_r, B_r)\) w naszych oczach. Światło zielone wywołuje jakiś inny wektor reakcji \(v_g\), a światło niebieskie jeszcze inny wektor reakcji \(v_b\). W związku z tym wszystkie możliwe reakcje, które monitor może wywołać w naszych oczach, to stożek generowany przez trzy elementy: wektory \(v_r\), \(v_g\) oraz \(v_b\) (tak naprawdę jeszcze dodatkowo ograniczony, bo monitor ma tylko 256 różnych nasileń światła i nie może też świecić dowolnie mocno, ale to z naszej perspektywy nieistotne). W szczególności niektóre możliwe reakcje z \(S_r\) nie dadzą się wywołać przez monitor. I to nie tylko taki, który ma trzy rodzaje pikseli, ale również taki, który miałby 10 albo 1000 rodzajów pikseli. Wciąż znajdą się jakieś reakcje na brzegu stożka reakcji \(S_r\), których nie da się wywołać przez sumowanie tych 1000 rodzajów pikseli!
Stożek \(S_r\) to zbiór wszystkich możliwych reakcji na światło, więc żaden fizyczny obiekt nie może mieć koloru, który wywołałby reakcję spoza \(S_r\). W szczególności nie jest możliwe stworzenie monitora, który generowałby zbiór większy niż stożek \(S_r\).
Specjaliści od grafiki starają się radzić sobie z tym fenomenem, jak mogą. Tworzą w szczególności różne skończenie generowane możliwe stożki barw: sRGB, AdobeRGB, ProPhotoRGB i inne, które lepiej lub gorzej przybliżają \(S_r\). Ale nigdy nie zrobią tego idealnie, bo jest to niemożliwe!
Więcej o stożkach barw można poczytać np. tu https://photographylife.com/srgb-vs-adobe-rgb-vs-prophoto-rgb.
Na koniec zapytajmy: to jakich kolorów nie przedstawia dobrze monitor? Generalnie stożkowi sRGB brakuje wielu kolorów na pograniczu niebieskiego i zielonego, przykładowo kolorów w okolicy cyjanowego. Tę sprawę polecam jednak badać na żywo, bo nie wszystko da się dostrzec w świecie wirtualnym.